This confuses me. How can the derivatives extend past the waveguide?
The idea could only be applied to a y(x) function that is single valued. Hence it could not be applied to a rollback such as the parameterized equations that are required in this case.There are several formula's for the OS. Mabat has x(t) and y(t), wikipedia has an y(x) (and some others). Which one do I have to differentiate twice to what variable?
I think that lower is the goal more than smooth. A smooth but high 2nd derivative will still have a lot of diffraction.If you're trying to get a smooth second derivative could you start with a clothoid?
I think it is along the waveguide / boundary.This confuses me. How can the derivatives extend past the waveguide?
But I think we're all a bit confused and trying hard to understand each other.
Yes, it is along the curve, I should have stated that. It's a parametric curve [x(t), y(t)], and of course we can still calculate its curvature (see below). If it was a curve as a function y(x), we would use just the derivatives of y(x)...
Curvature of y(x):
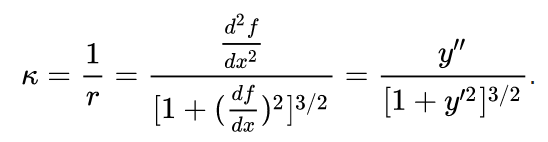
Curvature of [x(t), y(t)]:
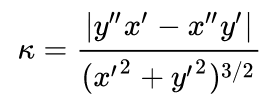
Curvature of y(x):
Curvature of [x(t), y(t)]:
Last edited:
So lowest possible diffraction is infinite tube?I think that lower is the goal more than smooth. A smooth but high 2nd derivative will still have a lot of diffraction.
The above shape:
Code:
OSSE = { ; #33/T34A-ROSSE
r0 = 19
a0 = 41.06
a = 71.25
k = 1.3
L = 19
s = 1.12
n = 2.467
q = 0.999
}I'd agree with that. The mouth diffraction has to be considered separately, but I think that the concept still applies. Marcel's parametric approach is interesting, I just haven't thought about things in those terms. It's not the way that I learned the physics.So lowest possible diffraction is infinite tube?
But yes, I can see that minimizing the curvature along the curve would certainly fit in with my understanding of diffraction.
The first OS waveguide that I built and tested (> 20 years ago) had a very sharp mouth termination. That's when I learned how important the mouth diffraction was. The diffract6ion ripples were obvious on top of what was clearly CD. Live and learn!
The idea could only be applied to a y(x) function that is single valued. Hence it could not be applied to a rollback such as the parameterized equations that are required in this case.
Ok, it's starting to make sense.
The catenary minimizes the potential energy a a chain. The potential energy is m*g*h (h = y), so linear in the height. The integral along the chain gives the total potential energy. The area of the surface of revolution is also linear in r (= x), so the surface is also minimal, right?
The function for a catenary is
by virtue of the exponentials the derivative and second derivative are easy. As a trivial example, the second derivative for a = 1 is equal to the function itself. If the diffraction is a linear function of the second derivative, that also means this curve minimizes the diffraction along the curve.
q.e.d. 😎
However, I'm not so sure the diffraction is a linear function of the second derivative. Somehow the curvature feels more natural...
Last edited:
Diffraction is a linear concept, although the diffraction is certainly frequency dependent, i.e. not linear in frequency. Two different things.However, I'm not so sure the diffraction is a linear function of the second derivative. Somehow the curvature feels more natural...
Straight line has always the least curvature, as well as the 2nd derivative (both=0). There must be more to this - the starting and terminating angles (vectors), but I have no clue how to incorporate those conditions into the equation.
Just pick the right section of a catenary (and the right 'a'). But you already solved that in your R-OSSE, right?
I really have no clue. These notion are far beyond me... I can't see how would such a task proceed.
Straight line has always the least curvature, as well as the 2nd derivative (both=0). There must be more to this - the starting and terminating angles (vectors), but I have no clue how to incorporate those conditions into the equation.
And an infinite cone driven by a spherical wavefront will have no diffraction. The fact that the throat wavefront is not spherical is why we must us OS-like surfaces at the throat - to match the wavefront, otherwise there is diffraction. Then there is the mouth, and likewise reality dictates flaring at the mouth.
A conical waveguide has zero 2nd derivative, but not a first.
Isn't the OS throat using diffraction to shape the wavefront, its just such a small distance the HOM's are above 20kHz?why we must us OS-like surfaces at the throat
Would it be possible to design with the crossover in mind, ie keep 2nd derivative flat at around 0 for as long as possible and only start increasing the rate of curvature after say 0.25x the wavelength of half an octave above x-frequency? As frequency increases sound becomes less 'diffractable' around the same curvature, so you can apply the principle of the sound separating power wise from the waveguide wall at higher freq, and then have lower power in the cross region, where the sound would most likely interact to generate HOMs with the termination of the waveguide.
Edit: I should say mouth reflections/diffraction artifacts not HOMs although it could apply.
Edit: I should say mouth reflections/diffraction artifacts not HOMs although it could apply.
Last edited:
I would say that the shape "allows" the shaping of the wavefront in a manner that is natural for it, i.e. the main mode. More modes are not desirable so minimizing them is critical to the final sound quality. Homs in a typical waveguide could be as low as 6 khz or maybe lower. Not a range to ignore. That's just modes in an infinite waveguide. Mode are created from reflections from the mouth - a standard wave sort of phenomena. But these mouth modes can be much much lower than that.Isn't the OS throat using diffraction to shape the wavefront, its just such a small distance the HOM's are above 20kHz?
Psychoacoustically, a significant diffraction will be heard as a secondary source and much more audible than a much lower level one even over a larger distance.
Do you have any support for this for this statement?
I am asking because when I designed the two waveguides here:
https://www.diyaudio.com/community/...he-easy-way-ath4.338806/page-575#post-7237263
I had a look at the curvature of the complete system, WG + Enclosure, and I was not quite sure what to make of the results i.e. what looks better.
I was comparing stitching a Bezier curve (blue, the first WG result of the optimization) vs extending the ROSSE profile all the way to close the enclosure (red identical WG up to the point of the enclosure taking over).
The red curvature (bottom right graph) is smoother but exhibits a discontinuity at the closing point vs the Blue curve with a milder discontinuity at the junction with the enclosure.
What do you think?
Regarding the throat shape, I see it as a continuum. Should be an exact OS shape a local minimum in some sense? It's hard to say, actually. When we look closely at the polars when the throat is changed smoothly, they also change smoothly, but it's actually difficult to say if the exact OS is the optimum. I realized that quickly after adding the parameter "k" into the formulae (k=2 means that an OS profile corresponding to twice the actual throat radius is used, i.e. it's no longer an OS coordinate system, despite using an OS curve).
This is a 1" throat for k = 0.5, k=1.0 (OS) and k=1.5:
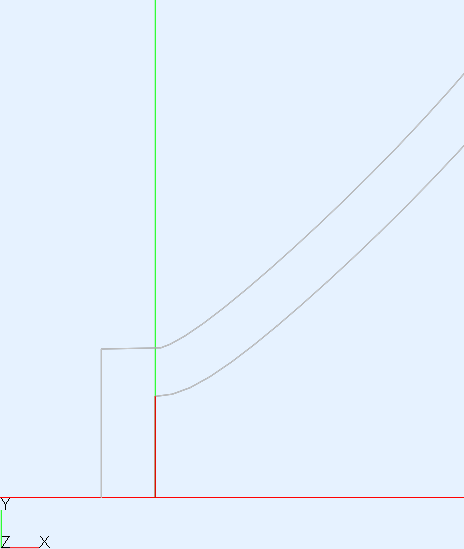
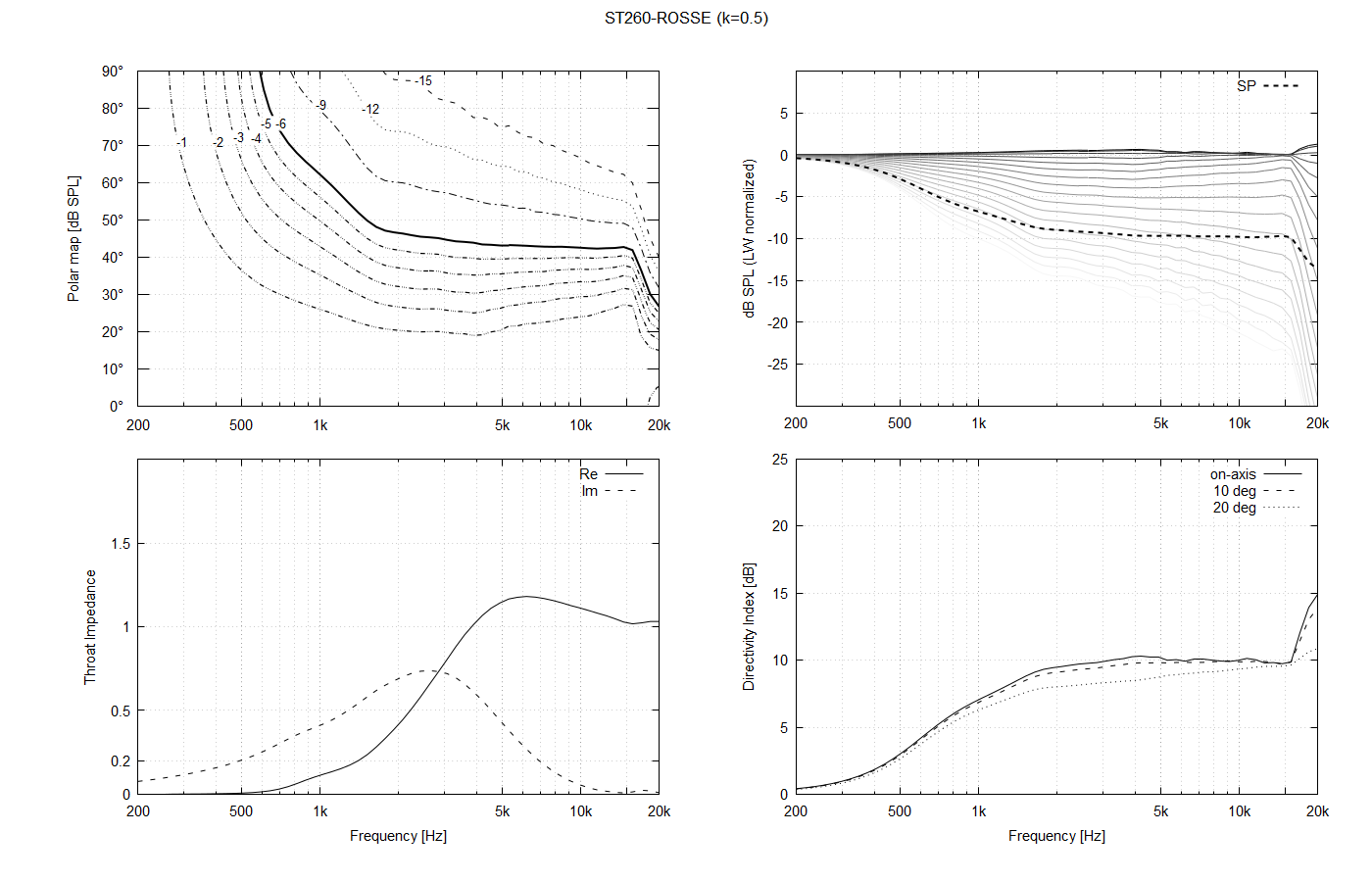
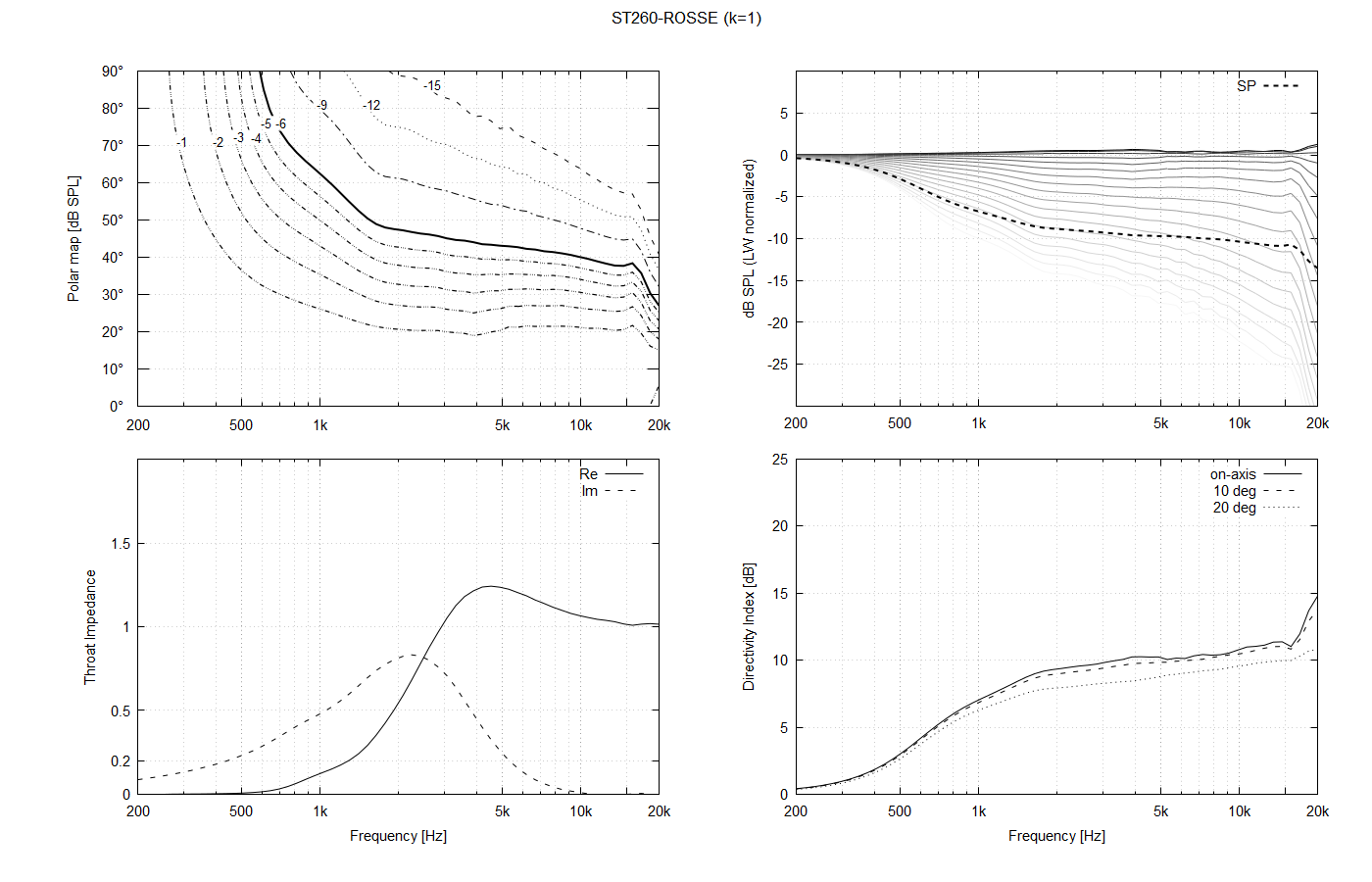
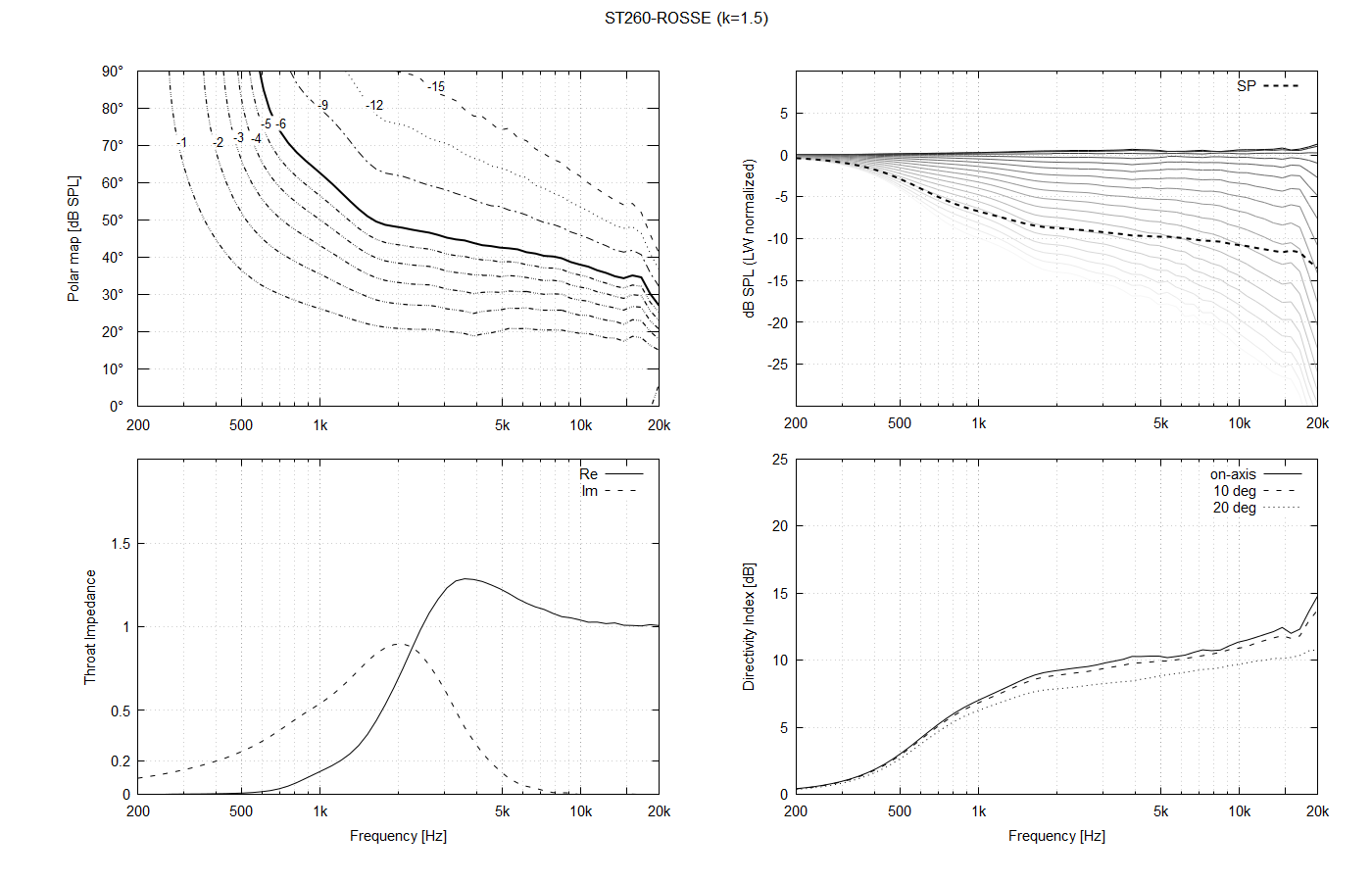
This is a 1" throat for k = 0.5, k=1.0 (OS) and k=1.5:
Last edited:
- Home
- Loudspeakers
- Multi-Way
- Acoustic Horn Design – The Easy Way (Ath4)