It should also have a proper definition, otherwise we're left with only a vague understanding (and quite easily also a misunderstanding).
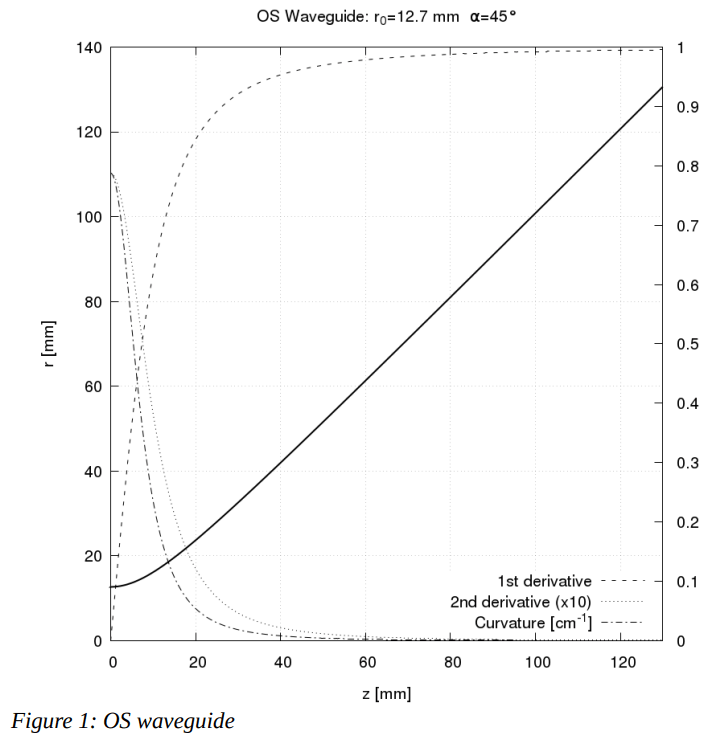
Changes in curvature are described by the derivative of curvature, that is k'(x)... 🙂
(But that's also a function, not a single number. How exactly do you minimize a function?)
- For example, an OS contour has a pretty high curvature change near the throat, but at the same time it is this curvature change what makes possible its constant-directivity behaviour... It is all quite complicated stuff.
Perhaps it is actually possible to formalize that vague idea, and then it would be fun to explore that further. That's why I ask.
Changes in curvature are described by the derivative of curvature, that is k'(x)... 🙂
(But that's also a function, not a single number. How exactly do you minimize a function?)
- For example, an OS contour has a pretty high curvature change near the throat, but at the same time it is this curvature change what makes possible its constant-directivity behaviour... It is all quite complicated stuff.
Perhaps it is actually possible to formalize that vague idea, and then it would be fun to explore that further. That's why I ask.
Last edited:
There are mathematical ways to minimize a function (given some target criteria like 0.0,) but I would simply say to average the function across its length (that would be like an integral.) Or maybe better yet take the SQR( sum of squares ) as a metric.(But that's also a function, not a single number. How exactly do you minimize a function?)
I think Mabat means that e.g. the curvature is a function (of z in the figure above). It is unclear what minimizing that function means.
I've never really understood what an OS minimizes and how that relates to diffraction and sound quality exactly. Is a very local, yet significant diffraction worse than little diffraction smeared out over a larger distance/area?
[I'm still searching for some quote, but can't find it...]
- One could find the z for which the function has the lowest value, but I doubt that what is what is meant.
- One could integrate the curvature along the shape and divide by its length, or some sort of RMS and then optimize the shape/curvature that minimizes the integral. Or should we integrate over the area of the waveguide?
I've never really understood what an OS minimizes and how that relates to diffraction and sound quality exactly. Is a very local, yet significant diffraction worse than little diffraction smeared out over a larger distance/area?
[I'm still searching for some quote, but can't find it...]
Well, can't we say an abrupt change in curvature is a "very local" surface feature that produces diffraction, and a constant change, that is "smearing", minimizes diffraction precisely through delocalization?Is a very local, yet significant diffraction worse than little diffraction smeared out over a larger distance/area?
The shape of the boundary is defined by the separable coordinate systems for the wave equation. This boundary will have to have the lowest 2nd derivative of any curve given the boundary conditions. It is what is known as a catenoid surface of revolution between two disks - minimum surface area. (But waveguides have to be terminated at some point and that termination, as shown throughout this thread, is critical.)I've never really understood what an OS minimizes and how that relates to diffraction and sound quality exactly. Is a very local, yet significant diffraction worse than little diffraction smeared out over a larger distance/area?
Psychoacoustically, a significant diffraction will be heard as a secondary source and much more audible than a much lower level one even over a larger distance.
I've just learned that the surround on T34B is actually convex, confirmed by Stanislav. Those who got a DXF from him, please be aware of that, that drawing is wrong. That makes the results I presented slightly worse and the T34A stays the better choice here, mainly for its height...
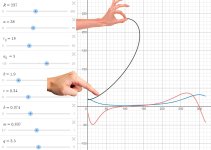
In the following Desmos graph blue is the curvature and red its derivative (rate of change), R-OSSE profile used:
https://www.desmos.com/calculator/hbsq4xght6
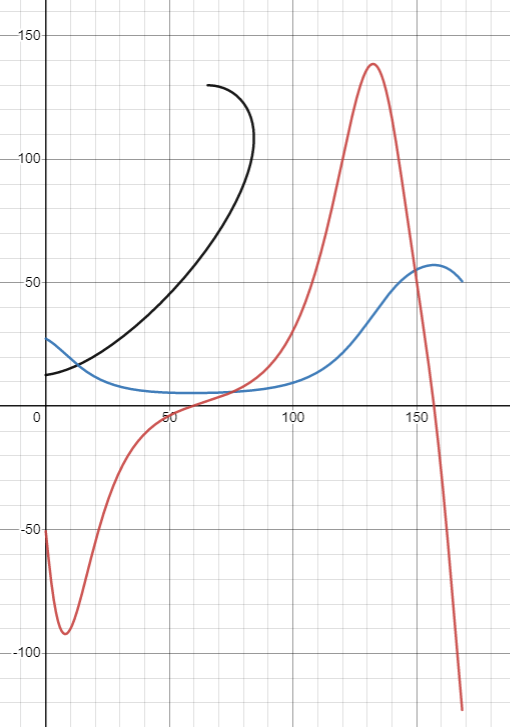
There's a room for an analysis... 🙂
https://www.desmos.com/calculator/hbsq4xght6
There's a room for an analysis... 🙂
How would you add conical exit section to this in Desmos, to see curvature on the driver/waveguide junction?
And thanks for these, very helpful!
And thanks for these, very helpful!
Conical duct has zero curvature so you can imagine that (and rate of change is not defined at the junction in that case)...
BTW, this middle plateau on the blue curve (the curvature) means that the central part of the profile is simply close to a circular arc:
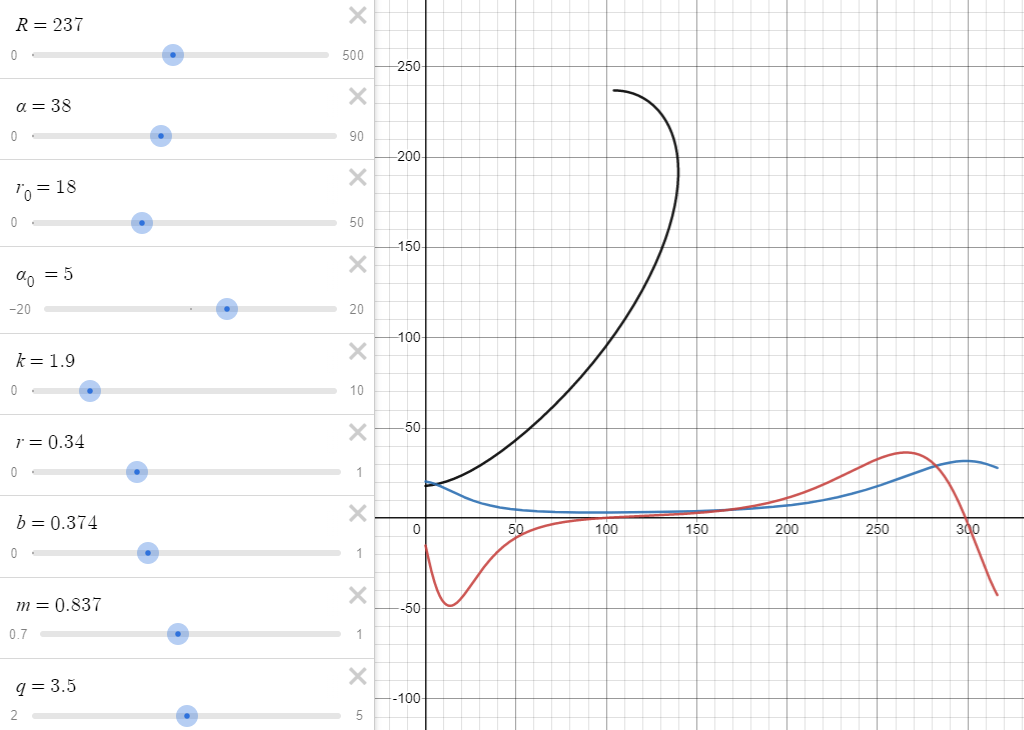
BTW, this middle plateau on the blue curve (the curvature) means that the central part of the profile is simply close to a circular arc:
Haha, well, nice 😀
So, when there is conical exit section the blue curve should start from origin to match conical exit to avoid big jump in curvature? to avoid reflection at throat junction
So, when there is conical exit section the blue curve should start from origin to match conical exit to avoid big jump in curvature? to avoid reflection at throat junction
Last edited:
Or use a ring plug.
- For high k / narrow coverage angles the R-OSSE profile is really just a circular arc for the most part (i.e. has a constant non-zero curvature):
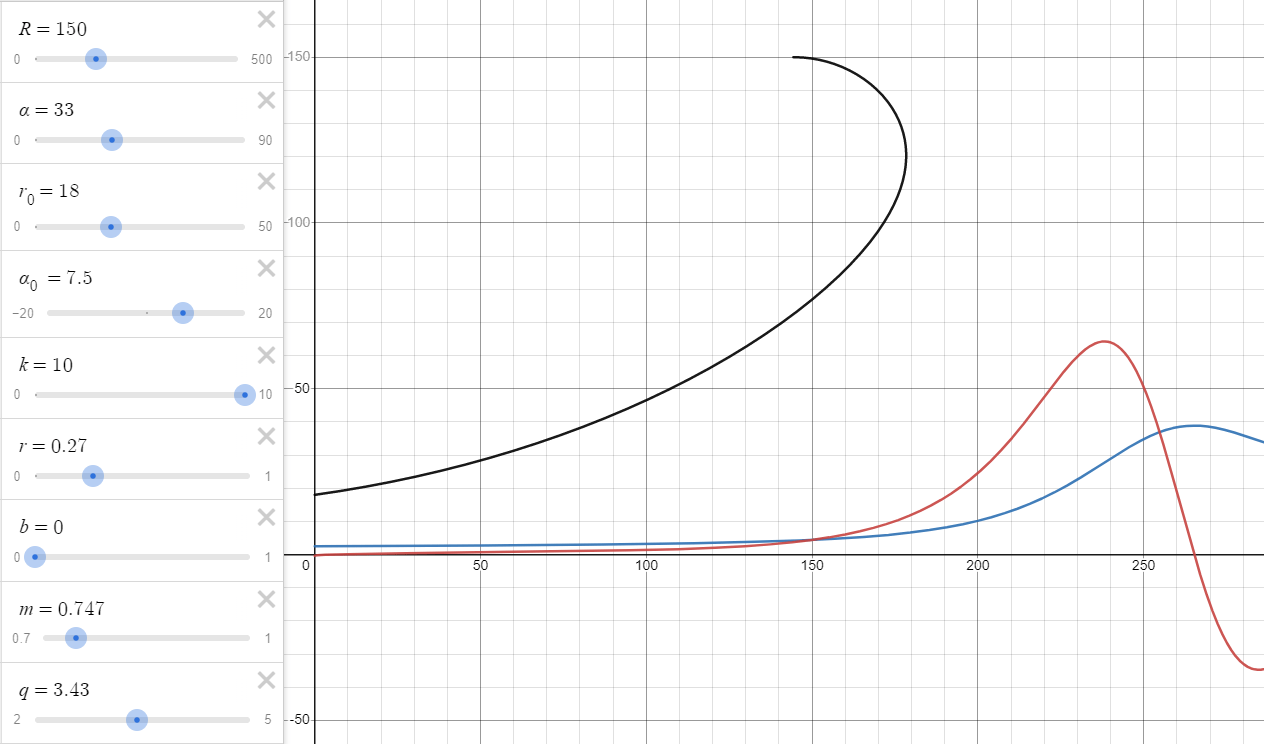
(I only wonder if this already has some other name... 🙂)
- For high k / narrow coverage angles the R-OSSE profile is really just a circular arc for the most part (i.e. has a constant non-zero curvature):
(I only wonder if this already has some other name... 🙂)
Last edited:
Haa, yes, "a beaming device" 🙂
I've found out its tough to affect curvature quite near the throat with R-OSSE, while the formula is quite flexible and gives lot of good results I've found it very difficult to get results I'm looking for with this conical throat stuff, with ring insert or not. Either there is angle at the throat (junction) or the device gets into beaming or some other anomaly appears. Perhaps this is inherent for such devices but somehow I always try to seek curve quite near throat never succeeding with it. k needs to be high but then can't get nice curve to it, I'd like to pinch on the end of the black line and pull it back or something 😀 I need to get back to the older OSSE formula and see if they had more control there.
I've found out its tough to affect curvature quite near the throat with R-OSSE, while the formula is quite flexible and gives lot of good results I've found it very difficult to get results I'm looking for with this conical throat stuff, with ring insert or not. Either there is angle at the throat (junction) or the device gets into beaming or some other anomaly appears. Perhaps this is inherent for such devices but somehow I always try to seek curve quite near throat never succeeding with it. k needs to be high but then can't get nice curve to it, I'd like to pinch on the end of the black line and pull it back or something 😀 I need to get back to the older OSSE formula and see if they had more control there.
Last edited:
OSSE and R-OSSE are really the same thing near the throat. It's the progression towards mouth that is different.
That's why I think it won't be so easy with the "2nd derivative" minimization. You can reduce that metric but end up with a more beaming device... (at least that's what I would expect)."a beaming device"
Last edited:
Something like this would be cool 😀 I can't seem to achieve this kind of bend close to throat with R-OSSE. Motivation would be to find something between beaming and discontinuity of curvature with conical throat. Ring insert yeah, but also there I'd like to bend bit more dramatically past the "throat". I've been playing with this quite a lot so its not from thin air, but at the same time I'm not sure if it would give any better results, its just something I'd like to try, feature I seem to grave and try to achieve but quite cannot. q -kind of affects this but then the rest of the curve goes bad and so on.
Do you have any hints how to achieve / hack it? I'm not sure if you have any motivation to use time on such thing as the formula seems to work well without? The math is beyond my skills

Do you have any hints how to achieve / hack it? I'm not sure if you have any motivation to use time on such thing as the formula seems to work well without? The math is beyond my skills
Last edited:
You can try that already with the Source.Contours feature - you can draw any part of the waveguide near the throat as a part of a source shape definition.
At least to get an idea.
(All the External Shaping Plug thing is done internally via Source.Contours. It's really a powerful feature.)
At least to get an idea.
(All the External Shaping Plug thing is done internally via Source.Contours. It's really a powerful feature.)
Last edited:
Thanks, there is so many features I could have just assumed there is some solution and seek for it 😀
I've got some more questions, but let's focus on this part:
There are several formula's for the OS. Mabat has x(t) and y(t), wikipedia has an y(x) (and some others). Which one do I have to differentiate twice to what variable?
This boundary will have to have the lowest 2nd derivative of any curve given the boundary conditions.
There are several formula's for the OS. Mabat has x(t) and y(t), wikipedia has an y(x) (and some others). Which one do I have to differentiate twice to what variable?
I would use curvature, which is an attribute of the shape itself, independent of its description.
Sometimes the 2nd derivative is used instead of curvature as a simplification.
Sometimes the 2nd derivative is used instead of curvature as a simplification.
Last edited:
If you're trying to get a smooth second derivative could you start with a clothoid? 2nd derivative should be a constant positive value, if curvature is increasing linearly down the length of the profile, then just morph from that starting point to get the desired level of constant directivity behaviour.
If you're trying to get a smooth second derivative could you start with a clothoid?
That's where I set out from some years ago, I actually used clothoids. The OSSE and R-OSSE profiles are the current culmination of this work - they are in fact very close to that and even a bit smoother overall, in principle.
"One of the most suitable curves for this purpose is the Euler spiral, also known as Cornu spiral or clothoid.
Although very effective, practical use of this curve can be somewhat difficult as it is not available in a simple
closed analytic form.
After some experimantation with the clothoids it was noticed that very similar results can be obtained by
adding a second function, representing a quadrant of a superellipse to the basic profile. The main advantage
of this approach is that it provides a simple closed-form function for the whole new profile, allowing an easy
manipulation in analytic form. Since the underlying profile and the termination is now smoothly blended
together, a completely seamless transition is achieved as the whole profile curve is infinitely differentiable. It
also makes the whole profile highly configurable by a simple and intuitive set of numerical parameters."
http://www.at-horns.eu/release/OS-SE Waveguide.pdf 🙂
Last edited:
- Home
- Loudspeakers
- Multi-Way
- Acoustic Horn Design – The Easy Way (Ath4)