@Tom Kamphuys : Generally, the matrix with (low) condition number 2.7 is relatively well-conditioned, which might help us solve the system of equations.
The other case with a humongous condition number says that it is ill-conditioned, and we probably might not be able to properly solve the system of equations the way we are trying to.
This sort of confirms my suspicion about what was going wrong with the measurements uniformly spaced in the circle. We might see that the condition number might be lower for the 2D case with randomized measurement locations.
Unfortunately, the condition number might help us only like a diagnostic tool as in the above case with the problem we are trying to solve, and there is not much else to do with it further.
The other case with a humongous condition number says that it is ill-conditioned, and we probably might not be able to properly solve the system of equations the way we are trying to.
This sort of confirms my suspicion about what was going wrong with the measurements uniformly spaced in the circle. We might see that the condition number might be lower for the 2D case with randomized measurement locations.
Unfortunately, the condition number might help us only like a diagnostic tool as in the above case with the problem we are trying to solve, and there is not much else to do with it further.
Please don't get too hung up on semantic discussions.
I suspect you are discussing without agreeing on the definition of terms.
Can we use it to optimize the measurement positions (by minimizing the condition number)?
Or is there something like the Chebyshev nodes for polynomials?
@Tom Kamphuys: Yes, we can keep a metric for optimization of measurement locations as the condition number and try.
But I am unsure whether that is the optimal metric for use in this use case or whether it will yield us practically usable measurement locations.
If we try to formally pose this as an optimization problem, I guess our objective function for the optimization is to minimize the condition number of the matrix "Psi" (using terminology from NTK's document) subject to the constraint that the measurement locations (functions of which fill up the matrix entries) lie between somewhere between 'x' cm to 'y' cm away from the source. However that problem looks very very complicated as the matrix dimensions grow fast with parameter 'N', and the condition number is a non-linear function of the matrix entries (determined by the measurement locations). So I don't have any hope of coming up with an easy analytical solution to that problem. We can probably try out some sane measurement positions and check if the condition number is low enough or not.
I am not much familiar with Chebyshev nodes but a quick google search showed that it is a projection of equispaced points on the unit circle onto the diameter of the circle. I don't think this would helps us since the measurement points will all lie on a line (at different radial distances probably but the angle not changing)
From your earlier experiment, it seemed like the randomization of measurement locations in the plane where we wanted to reconstruct the pressure field worked well, probably because it randomized the values determined by the spherical Hankel functions inside the matrix and resulted in a well conditioned matrix. But random locations like that maybe hard to implement in this usecase. So maybe we can explore some sort of structured way of reducing that radial dependency..
Example: Something like selecting 19 locations for measurement each location having a different radial distance from the source but angle changes uniformly by how many ever degrees we want (example 10 degrees). Let's say we start at 70cm away and increment the distance in 5cm steps. The next location is 75cm away, the next is 80 cm away and so on.. each time incrementing the angle also by 10 degrees)
I will try to look up if there is more structured way of doing this but also involve some amount of randomization? (At this point I don't know if I am even making any sense trying to describe this. But I will try)
But I am unsure whether that is the optimal metric for use in this use case or whether it will yield us practically usable measurement locations.
If we try to formally pose this as an optimization problem, I guess our objective function for the optimization is to minimize the condition number of the matrix "Psi" (using terminology from NTK's document) subject to the constraint that the measurement locations (functions of which fill up the matrix entries) lie between somewhere between 'x' cm to 'y' cm away from the source. However that problem looks very very complicated as the matrix dimensions grow fast with parameter 'N', and the condition number is a non-linear function of the matrix entries (determined by the measurement locations). So I don't have any hope of coming up with an easy analytical solution to that problem. We can probably try out some sane measurement positions and check if the condition number is low enough or not.
I am not much familiar with Chebyshev nodes but a quick google search showed that it is a projection of equispaced points on the unit circle onto the diameter of the circle. I don't think this would helps us since the measurement points will all lie on a line (at different radial distances probably but the angle not changing)
From your earlier experiment, it seemed like the randomization of measurement locations in the plane where we wanted to reconstruct the pressure field worked well, probably because it randomized the values determined by the spherical Hankel functions inside the matrix and resulted in a well conditioned matrix. But random locations like that maybe hard to implement in this usecase. So maybe we can explore some sort of structured way of reducing that radial dependency..
Example: Something like selecting 19 locations for measurement each location having a different radial distance from the source but angle changes uniformly by how many ever degrees we want (example 10 degrees). Let's say we start at 70cm away and increment the distance in 5cm steps. The next location is 75cm away, the next is 80 cm away and so on.. each time incrementing the angle also by 10 degrees)
I will try to look up if there is more structured way of doing this but also involve some amount of randomization? (At this point I don't know if I am even making any sense trying to describe this. But I will try)
Polynomials (order n) have the tendency to wiggle when a fit is performance through n points. When the points are the Chebyshev nodes, the wiggle of the fit is minimized. This is at least what I remember after 25 years. It's not exactly the same concept, but it would be nice to have good or optimal measurement positions.
After my hacking in a heuristic way, I'm trying to understand more what I'm doing.
These are the function I get for the 2D fit:
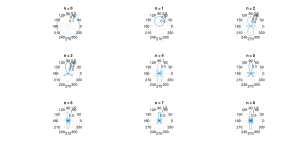
Unfortunately the legendre function in octave doesn't seem to result in these images. I use the spherical harmonics with m=0 and show the intersection of them with a plane.
n=1, 3, 5 and 7 seem to have two lines. You need to look closely Is that expected?
These are the function I get for the 2D fit:
Unfortunately the legendre function in octave doesn't seem to result in these images. I use the spherical harmonics with m=0 and show the intersection of them with a plane.
n=1, 3, 5 and 7 seem to have two lines. You need to look closely
Is that expected?
Which plane did you use for the intersection? A vertical one containing the z axis?
You might try using different colors for the positive and negative portions of the graphs. Many of the legendre polynomials have negative values over some range and putting those on a polar plot is tricky. Octave may ignore the sign and overlay the negative values on the positive ones. You might try a conventional plot of each legendre function vs. a straight theta axis to see if the functions look right.
Few
You might try using different colors for the positive and negative portions of the graphs. Many of the legendre polynomials have negative values over some range and putting those on a polar plot is tricky. Octave may ignore the sign and overlay the negative values on the positive ones. You might try a conventional plot of each legendre function vs. a straight theta axis to see if the functions look right.
Few
The Legendre polynomials are all symmetric for even index and antisymmetric for odd. For n = 1 the pattern is Cos(theta) which the plots do not show, so something is wrong.
I'd agree with this. Even though I have a deep background in acoustics, when I first heard the term "baffle step" it was new to me. You won't find it in any acoustics textbook - it was coined by audio people, not acousticians. When I figured out what it was, I realized that it was the simply the first order diffraction term for an enclosure (all enclosures diffract, aven a sphere.) It would be easy for someone who first learned about baffle step to not realize that it is caused by diffraction. The order that we learn things can affect our understanding of them.Please don't get too hung up on semantic discussions.
I suspect you are discussing without agreeing on the definition of terms.
Our assumptions or interpretation was wrong. Negative values of the 'legendre polynome' for an angle were plotted at the same position as positive values and an angle 180 degrees away.
In the mean time I implemented the legendre polynomials myself and plotted the absolute value and color-coded the sign of the values.
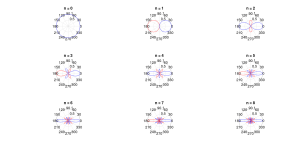
I'm also implementing a dedicated 2D version of NTK's stuff iso a handicapped 3D variant. Still some work to do.
I should have added that they do this at all frequencies, even very low. Of course at LFs only a very general shape is "seen" by the waves, but they do "see" it. The first order diffraction effect depends only on the volume of the enclosure, not its shape.
There was a study of this done by Stan Lipshitz at Waterloo - a few decades ago now. They used the "new" technique of BEM to compare an infinite baffled radiating source to one in a box and found correction terms that depended first on the volume, but more significant was the effect that depended on the area of the face, i.e. what we are calling the baffle step.
From the application of spherical harmonics to atomic orbitals I’m used to visualizing the legendre polynomials applied to the angle relative to a vertical z axis, and the complex exponentials wrapped around “the equator.”
For speaker directivity, is the primary radiation axis (sticking out horizontally from the front of the speaker) what would be the vertical z axis for the orbitals? So legendre polynomials are used to describe the behavior as a function of angle measured from the primary radiation axis, and complex exponentials are used to describe the behavior orbiting the speaker in a plane parallel to the speaker baffle? Am I picturing that correctly?
Few
For speaker directivity, is the primary radiation axis (sticking out horizontally from the front of the speaker) what would be the vertical z axis for the orbitals? So legendre polynomials are used to describe the behavior as a function of angle measured from the primary radiation axis, and complex exponentials are used to describe the behavior orbiting the speaker in a plane parallel to the speaker baffle? Am I picturing that correctly?
Few
I've been trying to visualize this also. I even looked into my old quantum mechanics books. I didn't get a warm and cozy feeling...
In the end, I don't think it matters. You could place the speaker in any orientation in the measuring volume and its sound field would be transformed into coefficients.
I'm still getting my head around this. Math is a summary of understanding to me. And a language to work with it. Unfortunately it doesn't explain thing to me. My current mental image is that the absolute value of a coefficient is the amplitude of that mode and the orientation is related to the phase. Similar to a Fourier transform.
Not sure if this helps. Maybe someone else can help us both.
In the end, I don't think it matters. You could place the speaker in any orientation in the measuring volume and its sound field would be transformed into coefficients.
I'm still getting my head around this. Math is a summary of understanding to me. And a language to work with it. Unfortunately it doesn't explain thing to me. My current mental image is that the absolute value of a coefficient is the amplitude of that mode and the orientation is related to the phase. Similar to a Fourier transform.
Not sure if this helps. Maybe someone else can help us both.
It is not my cup ofvtea, but thinking of Tom's statement about coefficient and visualising a soundwave observed at a point in space, amplitude yes, direction also, time also (i see phase as a math thing) , as sound to me is pressure variations moving along in a time continuüm, and reckognised by our hearing as something to listen to.
I think I'm slowly falling down Mount Stupid...
After typing my answer to @Few I started doubting my own words and tried to see what differs when I try to fit a 'rotated' dipole. My current algorithm can't :-( So something is clearly wrong. So first question:
- How is the mode (legendre polynomial order) rotated? Or phrased differently: What changes in the coefficients when my sound source (e.g. dipole) is rotated?
The other thing is about this page written by NTK:
In NTK's original code the difference between SFS and non-SFS was only using the outgoing 'mode' coefficients vs. all in reconstructing the sound field at the desired locations. In determining the coefficients all coefficients are calculated in both the SFS and non-SFS case. I thought that for the Gedlee-way I could leave out the incoming wave from the formula as that was done by filtering out echos in the IR. That would give me less unknowns and I would need fewer measurements. After some initial enthousiasm and heuristic high level thinking, I now would like to know how to do this exactly. Question two:
- Am I right that elimiting the incoming wave in fitting will benefit the amount of measurements needed? If so, how should I do that? What is the formula for p(r, theta, phi, omega)?
After typing my answer to @Few I started doubting my own words and tried to see what differs when I try to fit a 'rotated' dipole. My current algorithm can't :-( So something is clearly wrong. So first question:
- How is the mode (legendre polynomial order) rotated? Or phrased differently: What changes in the coefficients when my sound source (e.g. dipole) is rotated?
The other thing is about this page written by NTK:
In NTK's original code the difference between SFS and non-SFS was only using the outgoing 'mode' coefficients vs. all in reconstructing the sound field at the desired locations. In determining the coefficients all coefficients are calculated in both the SFS and non-SFS case. I thought that for the Gedlee-way I could leave out the incoming wave from the formula as that was done by filtering out echos in the IR. That would give me less unknowns and I would need fewer measurements. After some initial enthousiasm and heuristic high level thinking, I now would like to know how to do this exactly. Question two:
- Am I right that elimiting the incoming wave in fitting will benefit the amount of measurements needed? If so, how should I do that? What is the formula for p(r, theta, phi, omega)?
It feels a bit like laughing at your own jokes, but I'll add an answer and some insight wrt my own questions.
w.r.t. my second question: Weinreich gives the answer: B coefficients are zero.
wrt the first question: rotation
Here is how it is done for the spherical harmonics:
In the 2D variant we only have 1 function for a degree.
Is it as simple as using the knowledge that the sound source is a speaker and align the 'beams' of the legendre functions with the forward axis of the speaker?
w.r.t. my second question: Weinreich gives the answer: B coefficients are zero.
wrt the first question: rotation
Here is how it is done for the spherical harmonics:
In the 2D variant we only have 1 function for a degree.
Is it as simple as using the knowledge that the sound source is a speaker and align the 'beams' of the legendre functions with the forward axis of the speaker?
Because Earl’s description here says he uses legendre polynomials when fitting the pattern in a horizontal plane, I think the z axis has to be the direction the speaker is pointing.
Mathematically, I would think anything that is a basis in the relevant space can be forced to work, but a “good” basis should match the situation. As you found, if you want to be able to easily capture the monopole vs. dipole nature of the radiation, and the nodal pattern when the wavelength gets short at high frequencies, the legendre polynomials are a natural choice. Of course I stand ready to be straightened out if I’m off the mark!
Few
Mathematically, I would think anything that is a basis in the relevant space can be forced to work, but a “good” basis should match the situation. As you found, if you want to be able to easily capture the monopole vs. dipole nature of the radiation, and the nodal pattern when the wavelength gets short at high frequencies, the legendre polynomials are a natural choice. Of course I stand ready to be straightened out if I’m off the mark!
Few
Correct.
When we set m=0 we have assumed the source to be axisymmetric. This means that the z-axis needs to be aligned such that this assumption holds true as best it can. In everything that I measured this was nearly the case so this assumption was not a significant source of error, but in a completely general case there are situations where this assumption would be a serious error.
In full 3D no symmetry is assumed so this is not an issue and the source can be placed in any configuration, although convergence will be better if the main radiation axis is aligned with the z-axis.
Coming week my free time will be limited, so I'll give you guys a little teaser.
I read some angular measurement (10 degree steps) which was saved as txt in REW for use in VituixCAD into Octave. I looped over the frequencies and determined the coefficients and used them for evaluation at a denser grid (1 degree step).
Shoot!
I read some angular measurement (10 degree steps) which was saved as txt in REW for use in VituixCAD into Octave. I looped over the frequencies and determined the coefficients and used them for evaluation at a denser grid (1 degree step).
Shoot!