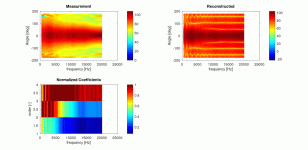
To me it looks like your coefficients above about 15 are noise. I almost never went that high as this kind of thing happens.
Also at the low end it seems like spurious level of the coefficients, which could be the singularity issue that I found - unstable matrix inversion. Small errors get amplified.
Also at the low end it seems like spurious level of the coefficients, which could be the singularity issue that I found - unstable matrix inversion. Small errors get amplified.
Well done! Obviously refinement will be necessary but you're making great headway!
Few
Few
Not sure what I am looking at. Interpolating the measured data does not sound like much, but I guess I am missing something.
Calculating an approximation of the directivity based on a best fit using the associated legendre polynomials is one of the main steps in the Klippel processing. Just by eyeing the plots it appears the legendre polynomials approximation captures the main features of the raw data.
Few
Few
I should point out that equal angular spacing is not optimum when doing fitting to the Legendre Polynomials. That's because the polys arguments are cos(theta) and not theta. For an optimum fit the angles should be equally spaced in cos(theta) - more angular resolution forward and less backward, which only makes sense since forward is where all the variations happen. I don't recall the exact spacing that used, but I am sure that I could find it and I'm sure that its on my website somewhere. I think it was 5 degrees to 25 then 10 to 60, then 20 - something like that. The exact values aren't critical.
To save Earl the trouble, from his website:
"0, 5, 10, 15, 20, 30, 40, 50, 60, 80, 100, 120, 150, 180 – 14 angles in total. "
"0, 5, 10, 15, 20, 30, 40, 50, 60, 80, 100, 120, 150, 180 – 14 angles in total. "
Those are standard polar angular measurements.
I may be imagining this incorrectly. From a measurement perspective, as you are closer to the nearfield you have less reflections as the dominant part of the signal. So are you saying that as you go farther away you need more randomized angular data? This makes sense to me. Interpolation of what you have as a nearfield reference. Nearfield will be our standard (and then as we go farther away we can generate an angular measurement with a correction factor?)
Yes
No, I don't see how the distance makes any difference. And the data points are never randomized - that would be sub-optimal.
There is no interpolation?!
I don't follow the issue.
You measure in the near field and fit the data to the nearfield polar modes. Then you use those modes to calculate what the far field data is from the nearfield measurements.
I never really did find a "solution", more like a work around. I simply fitted the LF data using a model based on Fs and Q of the woofer. In my system the results for LF always seem to blow up. I often wondered how Klippel dealt with this.
I assume that the code being used is using SVD, otherwise, it should as the matrix is clearly becoming singular at LFs. SVD will help, but even it has limitations.
I assume that the code being used is using SVD, otherwise, it should as the matrix is clearly becoming singular at LFs. SVD will help, but even it has limitations.
Ok, other than the interpolation being wrong we are speaking the same language Earl. I get it. This is what I gathered from NTK's explanations a few years ago. And you are shoring up my understanding. Thanks!
I would have naively thought that at low frequencies the directivity pattern would be simpler, with only large features (not much variation with angle) so life would be simpler. I’m no doubt revealing my novice status when it comes to singular value decomposition (SVD). I clearly have even more gaps to fill than I feared! Any intuitive explanation for why low frequencies are problematic?
Few
Few
It's simple, there basically are no differences from one measurement point to another at LFs. This means that the matrix to be inverted has rows that are nearly identical, in fact it has probably 14 of them. This means that they are not linearly independent making the matrix ill-conditioned and virtually singular. In fact one would guess, and this would be true, that only one mode should exist, namely the zeroth, the rest are redundant. Small errors in the data for higher modes get amplified by the math resulting in spurious values. At LFs there should only be the zeroth mode, but we see values randomly for the others. The plot that was shown shows this better than I could even describe.
I've often thought that the correct procedure would be to elliniate modes from the calcs as the frequency went down leaving just a single mode at the end. Or the other way, start with one and add ones in as their weighting factors get more significant. By weighting factor, I mean the modal impedances, if this impedance has a small magnitude then that mode is not contributing much and isn't needed. I did something like this in my code, but I was never satisfied. It could be looked at further, but not being a Matlab user, I am lost with code in that language.
I've often thought that the correct procedure would be to elliniate modes from the calcs as the frequency went down leaving just a single mode at the end. Or the other way, start with one and add ones in as their weighting factors get more significant. By weighting factor, I mean the modal impedances, if this impedance has a small magnitude then that mode is not contributing much and isn't needed. I did something like this in my code, but I was never satisfied. It could be looked at further, but not being a Matlab user, I am lost with code in that language.
Last edited:
Earl, maybe you measure in a very different room than I do. But low frequency measurements that are not in the nearfield, about 0.5m or less are totally dominated by your room and possible reflections that either enforce the response or null out the response. I'm definitely preaching to the choir. But it is not exactly the same everywhere. The no differences statement needs to have a distance associated with it.
It is true that at pretty much anything below about 150 hertz your driver and enclosure are shorter than the wavelength of sound being produced, so the system can be generalized as an omnidirectional source. But, what if you are working on a cardioid design? A low frequency horn? Transmission line? Back loaded horn. I could keep going. All of these are actually directional over parts of their passband are they not? Passband being 150 hertz to system Fc. From what I read in your reply to the low frequency problem I understood that you are taking a simulated system response and using this to fill in the troubling areas that your current method will not measure with clarity?
Mark
All the measurement points I was talking about are nearfield. They are the 14 points around the source - all nearfield, about half meter. For a monopole source these will all be nearly the same.
As I have said before all of my systems were monopoles so the problem that you raise never came up for me. I did once try and measure a dipole and my monopole assumption didn't work (of course!) These other source types can be done, it's just that not having any need for them I did not pursue it.
Yes, I did use simulated responses below about 150 Hz.
Thanks Earl.
So basically even a bass reflex is something that you were doing nearfield and integrating the port and the direct radiator via simulation.
Not something that I could actually do with all the design work I am up to. The REW moving mic method has as much or more utility. Nice to know that you have thought a bit about this for a while at least.
The Klippel clone we are trying to create is quite a bit more versatile I believe.
Understood.
So basically even a bass reflex is something that you were doing nearfield and integrating the port and the direct radiator via simulation.
Not something that I could actually do with all the design work I am up to. The REW moving mic method has as much or more utility. Nice to know that you have thought a bit about this for a while at least.
The Klippel clone we are trying to create is quite a bit more versatile I believe.
Understood.
Again, all I ever did were monopoles, I never did a bass reflex. As I said, I tried a dipole once and was not happy. All these other options need some carful considerations.
So fairly limited real world measuring experiences. I need to deal with whatever comes my way. Many times it is work that others are afraid to tackle. I love a challenge. And being independent, as you know all to well Earl, is not that easy when you need to pay bills. Why I am currently working on a kitchen and juggling three driver designs in the evenings, (China is 13 hours ahead of Eastern Standard Time right now) and dealing with Composite Sound for a dome off and on for a skunkwerks project. Nuttin but fun over here!
I wouldn't describe my "real world" measuring experiences as "limited". I've done a ton, of all kinds. Were talking about pretty advanced stuff here and I've only pushed the envelope in those places that I needed to.
The current micing technique used in automotive I developed some 40 years ago.
Here is an animated gif from Nmax = 3 to 24 in steps of 3
Please open to see it animated.
Please open to see it animated.