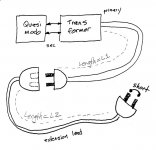
When shorting the primaries, does it matter if the primaries get shorted directly or if a power cord is attached, which then gets shorted?
Thanks!
Thanks!
Suppose the power cord is 1000 meters long, (longer than the transformer's primary winding). Would that affect the leakage inductance of the secondary?When shorting the primaries, does it matter if the primaries get shorted directly or if a power cord is attached, which then gets shorted?
Suppose the power cord is 100 meters long. Would that affect the leakage inductance of the secondary?
Suppose the power cord is 10 meters long. Would that affect the leakage inductance of the secondary?
1 meter long?
10 centimeters long?
1 centimeter long?
Suggest one or two ways to obtain the answers to these questions.
One could try measuring the ringing frequency.
What has me confused is that the formulas for leakage inductance can be written to include Rp.
What has me confused is that the formulas for leakage inductance can be written to include Rp.
Think of it as a brain teaser. Consider The Famous Barometer Problem and the unorthodox mode of thinking it encourages.
aaaaaand, the barometer problem's host website just crashed, no doubt caused by the tens of millions of page-hits from readers of the above DIYA post, who clicked the link and overwhelmed the server. Here is the contents of that page:
The Barometer Problem
by Alexander Calandra - an article from Current Science, Teacher's Edition, 1964.
Some time ago, I received a call from a colleague who asked if I would be the referee on the grading of an examination question. It seemed that he was about to give a student a zero for his answer to a physics question, while the student claimed he should receive a perfect score and would do so if the system were not set up against the student. The instructor and the student agreed to submit this to an impartial arbiter, and I was selected.
I went to my colleague's office and read the examination question, which was, "Show how it is possible to determine the height of a tall building with the aid of a barometer."
The student's answer was, "Take the barometer to the top of the building, attach a long rope to it, lower the barometer to the street, and then bring it up, measuring the length of the rope. The length of the rope is the height of the building."
Now, this is a very interesting answer, but should the student get credit for it? I pointed out that the student really had a strong case for full credit, since he had answered the question completely and correctly. On the other hand, if full credit were given, it could well contribute to a high grade for the student in his physics course. A high grade is supposed to certify that the student knows some physics, but the answer to the question did not confirm this. With this in mind, I suggested that the student have another try at answering the question. I was not surprised that my colleague agreed to this, but I was surprised that the student did.
Acting in terms of the agreement, I gave the student six minutes to answer the question, with the warning that the answer should show some knowledge of physics. At the end of five minutes, he had not written anything. I asked if he wished to give up, since I had another class to take care of, but he said no, he was not giving up. He had many answers to this problem; he was just thinking of the best one. I excused myself for interrupting him, and asked him to please go on. In the next minute, he dashed off his answer, which was:
"Take the barometer to the top of the building and lean over the edge of the roof. Drop the barometer, timing its fall with a stopwatch. Then, using the formula S= 1/2 at^2, calculate the height of the building."
At this point, I asked my colleague if he would give up. He conceded and I gave the student almost full credit. In leaving my colleague's office, I recalled that the student had said he had other answers to the problem, so I asked him what they were.
"Oh, yes," said the student. "There are many ways of getting the height of a tall building with the aid of a barometer. For example, you could take the barometer out on a sunny day and measure the height of the barometer, the length of its shadow, and the length of the shadow of the building, and by the use of simple proportion, determine the height of the building."
"Fine," I said. "And the others?"
"Yes," said the student. "There is a very basic measurement method that you will like. In this method, you take the barometer and begin to walk up the stairs. As you climb the stairs, you mark off the length of the barometer along the wall. You then count the number of marks, and this will give you the height of the building in barometer units. A very direct method.
"Of course, if you want a more sophisticated method, you can tie the barometer to the end of a string, swing it as a pendulum, and determine the value of 'g' at the street level and at the top of the building. From the difference between the two values of 'g', the height of the building can, in principle, be calculated."
Finally, he concluded, "If you don't limit me to physics solutions to this problem, there are many other answers, such as taking the barometer to the basement and knocking on the superintendent's door. When the superintendent answers, you speak to him as follows: 'Dear Mr. Superintendent, here I have a very fine barometer. If you will tell me the height of this building, I will give you this barometer.'"
At this point, I asked the student if he really didn't know the answer to the problem. He admitted that he did, but that he was so fed up with college instructors trying to teach him how to think and to use critical thinking, instead of showing him the structure of the subject matter, that he decided to take off on what he regarded mostly as a sham.
The Barometer Problem
by Alexander Calandra - an article from Current Science, Teacher's Edition, 1964.
Some time ago, I received a call from a colleague who asked if I would be the referee on the grading of an examination question. It seemed that he was about to give a student a zero for his answer to a physics question, while the student claimed he should receive a perfect score and would do so if the system were not set up against the student. The instructor and the student agreed to submit this to an impartial arbiter, and I was selected.
I went to my colleague's office and read the examination question, which was, "Show how it is possible to determine the height of a tall building with the aid of a barometer."
The student's answer was, "Take the barometer to the top of the building, attach a long rope to it, lower the barometer to the street, and then bring it up, measuring the length of the rope. The length of the rope is the height of the building."
Now, this is a very interesting answer, but should the student get credit for it? I pointed out that the student really had a strong case for full credit, since he had answered the question completely and correctly. On the other hand, if full credit were given, it could well contribute to a high grade for the student in his physics course. A high grade is supposed to certify that the student knows some physics, but the answer to the question did not confirm this. With this in mind, I suggested that the student have another try at answering the question. I was not surprised that my colleague agreed to this, but I was surprised that the student did.
Acting in terms of the agreement, I gave the student six minutes to answer the question, with the warning that the answer should show some knowledge of physics. At the end of five minutes, he had not written anything. I asked if he wished to give up, since I had another class to take care of, but he said no, he was not giving up. He had many answers to this problem; he was just thinking of the best one. I excused myself for interrupting him, and asked him to please go on. In the next minute, he dashed off his answer, which was:
"Take the barometer to the top of the building and lean over the edge of the roof. Drop the barometer, timing its fall with a stopwatch. Then, using the formula S= 1/2 at^2, calculate the height of the building."
At this point, I asked my colleague if he would give up. He conceded and I gave the student almost full credit. In leaving my colleague's office, I recalled that the student had said he had other answers to the problem, so I asked him what they were.
"Oh, yes," said the student. "There are many ways of getting the height of a tall building with the aid of a barometer. For example, you could take the barometer out on a sunny day and measure the height of the barometer, the length of its shadow, and the length of the shadow of the building, and by the use of simple proportion, determine the height of the building."
"Fine," I said. "And the others?"
"Yes," said the student. "There is a very basic measurement method that you will like. In this method, you take the barometer and begin to walk up the stairs. As you climb the stairs, you mark off the length of the barometer along the wall. You then count the number of marks, and this will give you the height of the building in barometer units. A very direct method.
"Of course, if you want a more sophisticated method, you can tie the barometer to the end of a string, swing it as a pendulum, and determine the value of 'g' at the street level and at the top of the building. From the difference between the two values of 'g', the height of the building can, in principle, be calculated."
Finally, he concluded, "If you don't limit me to physics solutions to this problem, there are many other answers, such as taking the barometer to the basement and knocking on the superintendent's door. When the superintendent answers, you speak to him as follows: 'Dear Mr. Superintendent, here I have a very fine barometer. If you will tell me the height of this building, I will give you this barometer.'"
At this point, I asked the student if he really didn't know the answer to the problem. He admitted that he did, but that he was so fed up with college instructors trying to teach him how to think and to use critical thinking, instead of showing him the structure of the subject matter, that he decided to take off on what he regarded mostly as a sham.
When shorting the primaries, does it matter if the primaries get shorted directly or if a power cord is attached, which then gets shorted?!
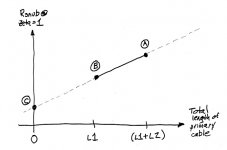
After considering the Barometer Problem for a while, the verb "extrapolate" might pop into your head, suggesting the following plan:
1. Short the plug, connect to Quasimodo, adjust for Zeta=1 damping. Measure Rsnub. This is measurement "B".
2. Connect an "extension lead" (extension cord?) to the power cord. Now the cord is longer. Short the plug, connect to Quasimodo, adjust for Zeta=1 damping. Measure Rsnub. This is measurement "A".
3. Plot Rsnub versus total lead length. Extrapolate on the plot to Length=0. This is point "C".
4. Ask and answer the question, "Just how confident am I, in this result?"
2. Connect an "extension lead" (extension cord?) to the power cord. Now the cord is longer. Short the plug, connect to Quasimodo, adjust for Zeta=1 damping. Measure Rsnub. This is measurement "A".
3. Plot Rsnub versus total lead length. Extrapolate on the plot to Length=0. This is point "C".
4. Ask and answer the question, "Just how confident am I, in this result?"
Attachments
Quasimodo V4 through hole kit
Have Quasimodo V4 through hole version kits for sale in stock. The kit is 29USD with free shipping to the lower states. The kit is standard BOM. The boards are with ENIG finish. Parts are labeled and packaged in small plastic bags.
Have Quasimodo V4 through hole version kits for sale in stock. The kit is 29USD with free shipping to the lower states. The kit is standard BOM. The boards are with ENIG finish. Parts are labeled and packaged in small plastic bags.
It might be a good use of your time to review the attachments connected with post #1 in this thread.Is 12 VDC enough to power Quasimodo?
I often wonder, "Is it a bad idea to reward laziness?" "Does this encourage further laziness?". What is your opinion, if I may ask?
Attachments
It works with two old 9V batteries, back to back giving about 14.5 volts.
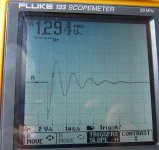
It appears that optimizing 5 secondaries in parallel ( a five channel HT toroid ) shows a sawtooth superimposed on a sine wave decreasing in amplitude, but when it rings, they all ring in concert.
It appears that optimizing 5 secondaries in parallel ( a five channel HT toroid ) shows a sawtooth superimposed on a sine wave decreasing in amplitude, but when it rings, they all ring in concert.
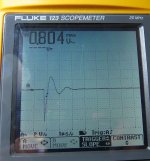
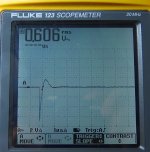
Three shots. The first is 18.5 ohms. It's 0.2 V/Div. The second is 0 ohms at 5 V/div, the final is infinite ( no trimmer ) at 5 V/div.
These are all B channel, having triggered on A channel.
What confuses me is the dead short. Unfortunately, I did not photograph it at 0.2 V/div, and my daughter just left with her cell phone....
This toroid has five CT secondaries in parallel. For this test, they were wired with the one secondary connected to the CT. They all seems to ring together.
These are all B channel, having triggered on A channel.
What confuses me is the dead short. Unfortunately, I did not photograph it at 0.2 V/div, and my daughter just left with her cell phone....
This toroid has five CT secondaries in parallel. For this test, they were wired with the one secondary connected to the CT. They all seems to ring together.
Attachments
Last edited:
It's kind of a shame that your first experiment with Quasimodo didn't give a clear and unambiguous answer to the question "Does my Quasimodo board work correctly? Is mine stuffed and soldered erroneously?"
Maybe you can dream up a test protocol that would validate or invalidate your QM board, without the confounding presence of five parallel center-tapped secondaries.
Maybe you can dream up a test protocol that would validate or invalidate your QM board, without the confounding presence of five parallel center-tapped secondaries.
I've ordered a new scope, as this one is a POS. It took HOURS to get those pics.
I suppose, the best way to test is one secondary at a time, but I'm not going to use it that way.
The A channel shows a nice impulse, and the CT is shorted to the unused secondary. Let's wait until the new scope arrives. This one is a pain.
I suppose, the best way to test is one secondary at a time, but I'm not going to use it that way.
The A channel shows a nice impulse, and the CT is shorted to the unused secondary. Let's wait until the new scope arrives. This one is a pain.
You might want to order one of these too. It's cheap and it's 5% tolerance.
Of course they have lots of different parts to choose from (link)
Of course they have lots of different parts to choose from (link)
I have a couple of small transformers lying around as well.
A 12 V @ 12 VA and a larger 18 volt 216 VA, both with two secondaries.
And a big 5A Hammond choke.
A 12 V @ 12 VA and a larger 18 volt 216 VA, both with two secondaries.
And a big 5A Hammond choke.
another one working
I've used snubbers on transformers for years so I've been following this thread with interest for a while. I always roughly guessed at the right values assuming that they exact value wasn't that critical.
I recently bought a v4 board and kit of parts from dsolodov and threw together a kit. It works great. Thanks to Mark for the clever design and for sharing it with all of us.
To test it out, I grabbed an Antek AS-0512 toroid that I recently bought. It's a 50VA transformer with dual 120v primaries and dual 12v secondaries. I shorted out the two primaries and one of the 12v secondaries and then tested things with the ringer. I used 10nf for C2/Cx and 150nf for C3/Cs. The pictures below show with the damping resistance open, 56ohms, and 22ohms. The optimal Rs seems to be 22ohms. I was also interested in what happens without Cx. So I used a 330pf cap for C2 and also changed C3 to 22nf, which is a value I've often used in the past. Optimal Rs for this case was ~88ohms, but it wasn't as clean as when using the larger Cx.
---Gary
I've used snubbers on transformers for years so I've been following this thread with interest for a while. I always roughly guessed at the right values assuming that they exact value wasn't that critical.
I recently bought a v4 board and kit of parts from dsolodov and threw together a kit. It works great. Thanks to Mark for the clever design and for sharing it with all of us.
To test it out, I grabbed an Antek AS-0512 toroid that I recently bought. It's a 50VA transformer with dual 120v primaries and dual 12v secondaries. I shorted out the two primaries and one of the 12v secondaries and then tested things with the ringer. I used 10nf for C2/Cx and 150nf for C3/Cs. The pictures below show with the damping resistance open, 56ohms, and 22ohms. The optimal Rs seems to be 22ohms. I was also interested in what happens without Cx. So I used a 330pf cap for C2 and also changed C3 to 22nf, which is a value I've often used in the past. Optimal Rs for this case was ~88ohms, but it wasn't as clean as when using the larger Cx.
---Gary
Attachments
Congratulations GaryB! Your wiggles look good.
Apparently secondary windings which output low voltages (like 12V), tend to have less leakage inductance. So the sqrt(L/Cx) "characteristic impedance" is lower and the optimal snubbing resistance is lower.
Apparently secondary windings which output low voltages (like 12V), tend to have less leakage inductance. So the sqrt(L/Cx) "characteristic impedance" is lower and the optimal snubbing resistance is lower.
- Home
- Amplifiers
- Power Supplies
- Simple, no-math transformer snubber using Quasimodo test-jig