Quasimodo tests vs. theoretical formula
I've been using the Quasimodo jig for some time, and have presented the results in a non-English speaking forum (a Serbian one, as a matter of fact). Mark kindly allowed to have his design published in this forum, and it generated interest there. However, the need to have a scope in order to use the Quasimodo jig was quite an obstacle for most of the forum members, so I set out to establish whether a method based on theory and a measurement of the inductance (there are cheap LCR meters about) and the secondary resistance would produce similar results as the experimental one. The investigation generated very interesting data, which I hope could be of value to a broader audience.
The formula I used to calculate the value of Rs was the one from p. 9 of the Hagerman's paper (http://www.hagtech.com/pdf/snubber.pdf) because it also takes into account the secondary resistance.
I tested a total of 9 transformers in the process, out of which one was measured with and without a rectifier. The results are summarized in the Excel file attached. The last row in the table makes it possible to calculate the Rs value with one's own data.
Referring to the table, I calculated the inductance (col. E) from the frequency of the first natural mode of the circuit, i.e. without the Rs trimmer in place. I also determined the natural damping factor from the logarithmic decrement, as described in Appendix B of the Mark's design note. Then I determined the frequency of the second natural mode (at Rs=0) because I wanted to see how the circuit behaves without Rs (s. my post #308). I found out that three of the transformers tested are actually already quite damped in this mode, albeit not optimally.
The last two columns compare the values of Rs arrived at with the Quasimodo jig (col. I), and by applying the Hagermann's formula (col. J). In most cases, the agreement is quite good, which was good news for the forum members.
The discrepancy between the two resistances in the first row of the table stems from the fact that the value Rs=670R was due to my decision to set it at the arithmetic mean between the values I obtained with Quasimodo at the points where the respective mode 1 and 2 oscillation were optimally damped (I discussed this with Mark around the post I previously mentioned). Since the transformer was already built into the power supply at the time this investigation was carried out, I did not want to change this value any more, but I checked the waveform at the rectifier in operation and found no ringing.
The Hammond 162F36 proved a rather difficult customer in that the point of optimum damping was difficult to establish. The low Rs value is a bit of a worry, so I will have to experiment with a different value of Cs here.
In conclusion, for people without a scope, the theoretical formula is a very useful solution provided that the LCR meter available is up to the job. This, however, I haven't been able to test for lack of time.
Regards,
Braca
I've been using the Quasimodo jig for some time, and have presented the results in a non-English speaking forum (a Serbian one, as a matter of fact). Mark kindly allowed to have his design published in this forum, and it generated interest there. However, the need to have a scope in order to use the Quasimodo jig was quite an obstacle for most of the forum members, so I set out to establish whether a method based on theory and a measurement of the inductance (there are cheap LCR meters about) and the secondary resistance would produce similar results as the experimental one. The investigation generated very interesting data, which I hope could be of value to a broader audience.
The formula I used to calculate the value of Rs was the one from p. 9 of the Hagerman's paper (http://www.hagtech.com/pdf/snubber.pdf) because it also takes into account the secondary resistance.
I tested a total of 9 transformers in the process, out of which one was measured with and without a rectifier. The results are summarized in the Excel file attached. The last row in the table makes it possible to calculate the Rs value with one's own data.
Referring to the table, I calculated the inductance (col. E) from the frequency of the first natural mode of the circuit, i.e. without the Rs trimmer in place. I also determined the natural damping factor from the logarithmic decrement, as described in Appendix B of the Mark's design note. Then I determined the frequency of the second natural mode (at Rs=0) because I wanted to see how the circuit behaves without Rs (s. my post #308). I found out that three of the transformers tested are actually already quite damped in this mode, albeit not optimally.
The last two columns compare the values of Rs arrived at with the Quasimodo jig (col. I), and by applying the Hagermann's formula (col. J). In most cases, the agreement is quite good, which was good news for the forum members.
The discrepancy between the two resistances in the first row of the table stems from the fact that the value Rs=670R was due to my decision to set it at the arithmetic mean between the values I obtained with Quasimodo at the points where the respective mode 1 and 2 oscillation were optimally damped (I discussed this with Mark around the post I previously mentioned). Since the transformer was already built into the power supply at the time this investigation was carried out, I did not want to change this value any more, but I checked the waveform at the rectifier in operation and found no ringing.
The Hammond 162F36 proved a rather difficult customer in that the point of optimum damping was difficult to establish. The low Rs value is a bit of a worry, so I will have to experiment with a different value of Cs here.
In conclusion, for people without a scope, the theoretical formula is a very useful solution provided that the LCR meter available is up to the job. This, however, I haven't been able to test for lack of time.
Regards,
Braca
I did compare LCR measurements vs Quasimodo measurements (post #375), I also tried the comparison on a number of transformers I have and the result generally match well.
I find it difficult to use Quasimodo as an inductance measurement tool, as I got optimum damping over a range of R values, often spanning 25% above/below the theoretical value, and it's not easy to tell when zeta equals one.
However, if the goal is to find a snubber which damp the transformer properly, Quasimodo is great as it takes into account the actual inductance and capacitance in the power supply including the rectifier bridge, and you know it's working by looking at the damping in action through the scope.
If you want to measure inductance, try the linear regression method outlined in Appendix C of the Quasimodo design note. Take at least 5 datapoints for numerical robustness. I find it agrees with LCR readings, and both of them agree with the inductor manufacturer's stated value (plus or minus the stated tolerance).
Of course, this requires that you know the test capacitors' values (at the resonant frequency (1/2pi)*sqrt(L/C)) relatively accurately. I use tight tolerance CP0-ceramic caps for these measurements.
Last edited:
I tried this too, and did not have good success. I used an Agilent LCR meter and a half dozen transformers, but never got repeatable or self-consistent results. You are probably more skillful than me. By contrast, I find Quasimodo gives the same answer every time; when I change scopes, when I change capacitors, and when I change Vcc from 3V to 17V and everywhere in between, I keep getting the same value of Rdamping.
I think it's worth remembering that Hagerman assumes his readers are somewhat familiar with the differential equations used by professional electrical engineers. He suggests a target zeta (sqrt(1/2)=0.707) which is underdamped; in my opinion, this target is too dangerous for hobbyists, beginners, and your particular audience: people who don't even have access to an oscilloscope. It is dangerous because if you happen to miss the target on the low side, you get some seriously underdamped behavior. Instead, I prefer to recommend that beginners, hobbyists, and non-EEs should aim for zeta=1. If, through human error, you miss the target by as much as a factor of two, on either side, damping is still acceptable. Zeta=1 is a more forgiving target; there's a greater safety margin all around it.
Professional EEs, on the other hand, don't need any advice from me; they can design to whatever value of zeta they please. Since the transformer secondary circuit is a second order system, these folks can make a Q-to-zeta calculation and wind up with "Butterworth alignment" snubbers, "Bessel alignment" snubbers, and more. Impressive and fancy!
I suppose you're referring to a missing *.xls file. Well, attachments with active contents are not allowed in the forum unless they are compressed.
I hope the zipped attachment i'm now enclosing will be ok for you.
Regards,
Braca
I agree, but the pupose of the investigation was to test the method. People using the Excel sheet can simply set Zeta=1 in the cell G3, obtaining thus the corresponding Rs value.
Regards,
Braca
I forgot to mention that all frequencies quoted in the attachment were obtained by means of the Quasimodo jig and a scope by simply reading off the time over (typically) three periods of the naturally damped oscillations following the Quasimodo pulse, and converting the reading to frequency. They thus represent the respective average values over three periods.
I am yet to test the other side of the method, namely measuring the inductance by means of an LCR meter. Thanks for the remark re. your experience with this kind of measurement
Regards,
Braca
DNi, I think it would be a good idea for you to ask the diyAudio moderators to move your spreadsheet posts (#444 and #451) into their own thread with its own title, and with you as the Original Poster. I am sure you are able to think of your own title and need no suggestions from me, but here is a suggestion anyway:
Here is a Way to Design a Transformer Snubber, using No Math and No Oscilloscope
Thank you for your suggestion, Mark. I thought about starting a new thread too, but I came to the conclusion that a new thread dealing with transformer snubbing is not really warranted. The subject to be dealt with in relation to my Excel file is the measurement of the transformer parasitic inductance without a scope, and since I am at the moment not able to pursue this subject, I must refrain from opening such a thread.
As regards my files, I hope they are not seen as off-topic in this thread, but rather as an addition to the work you've done on the subject of transformer snubbing. All measurements were done with Quasimodo, and we see that a simple measurement of the natural frequency based on reading the time between a few periods off the scope screen, which then leads on to the parasitic inductance, is adequate for calculating the snubber resistance that agrees well with the result obtained by adjusting the value of Rs until the proper damped response is attained.
I see the above as a simplification of the mathematical procedure for determining the value of Rs that you described in your design note. Whether it be used as a check on the Rs value obtained experimentally or as a method in itself is up to the user.
Reagards,
Braca
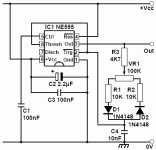
Looking for the right transformer polarity, attached pics left to right:
1st pic schematic used
2nd pic scope probe direct to NE555 astable output (not connected to transformer).
3rd pic scope probe to undotted secondary transformer, signal connected to
dotted secondary.
4th pic scope probe to dotted secondary transformer, signal connected to undotted secondary.
What I'm missing or I'm doing something wrong (primary transformer is shorted also the 2nd secondary is also shorted.
TIA
Felipe
1st pic schematic used
2nd pic scope probe direct to NE555 astable output (not connected to transformer).
3rd pic scope probe to undotted secondary transformer, signal connected to
dotted secondary.
4th pic scope probe to dotted secondary transformer, signal connected to undotted secondary.
What I'm missing or I'm doing something wrong (primary transformer is shorted also the 2nd secondary is also shorted.
TIA
Felipe
Attachments
![WP_20140925_001[1].jpg](/community/data/attachments/409/409581-acbf424913f784592dac9cf00a977702.jpg)
![WP_20140925_002[1].jpg](/community/data/attachments/409/409589-9686a19d4d01c56f21f96d111eb12285.jpg)
![WP_20140925_003[1].jpg](/community/data/attachments/409/409595-99d90aeecd1c23aa62c39a9fa88a2423.jpg)
You need to learn about transformer polarity "dots". Among the many search hits that Google provides, you definitely need to study
- The Wikipedia article
- The YouTube video by Lutfi Al-Sharif , 5/11/2013
- The article on ElectricalTechnology.org: Transformer Phasing, the Dot Notation
- The Maplesoft article on Coupled Inductors