Now we want to find out very quickly whether there is actually a gain between the termination with 150kOhm compared to the standard 47kOhm - and ask noise_1_3.exe for advice. The OPA627 serves as our DUT.
1)
OPu=8e-9
OPi=1.6e-15
G1k=
Rq=12e3
Ltc=
Rdc=
R1=47e3
R2=
R3=
df=
T=27
99.0099 5000000 9559.322 10000 100 12000 47000
3.173164e-008[V] 3.204896e-006[V] 101.888[dB]
1.08458e-006[V] 0.0001095426[V] 71.21266[dB]
short 4.66499e-005[V] 80.60239[dB]
open 4.665196e-005[V] 80.60201[dB]
infinite 4.665004e-005[V] 80.60236[dB] Riq= 12000[Ohm]
reference: 0.3983051[V] 8.726267e-005[V] 73.18774[dB]
reference: 0.3983051[V] 0.000202697[V] 65.86737[dB]
3864.734[V/A] 7.999999811618085e-009[V/sqrt(Hz)]
1.545893761867023e-010[A/V] 1.600000019001911e-015[A/sqrt(Hz)]
124.4740146547698[dB] 6.46875e+009[Ohm]
2)
OPu=8e-9
OPi=1.6e-15
G1k=
Rq=12e3
Ltc=
Rdc=
R1=150e3
R2=
R3=
df=
T=27
99.0099 5000000 11111.11 10000 100 12000 150000
3.687701e-008[V] 3.724578e-006[V] 101.8894[dB]
9.851904e-007[V] 9.950423e-005[V] 73.3541[dB]
short 4.66499e-005[V] 80.60239[dB]
open 4.667089e-005[V] 80.59848[dB]
infinite 4.665004e-005[V] 80.60236[dB] Riq= 12000[Ohm]
reference: 0.462963[V] 9.213348e-005[V] 74.02258[dB]
reference: 0.462963[V] 0.0003147775[V] 63.35085[dB]
3864.734[V/A] 7.999999811618085e-009[V/sqrt(Hz)]
1.545893761867023e-010[A/V] 1.600000019001911e-015[A/sqrt(Hz)]
124.4740146547698[dB] 6.46875e+009[Ohm]
OPu=
C:\Windows\System32>
Nevertheless, a 150kOhm resistor produces more thermal noise than a 47kOhm resistor, the trick is hidden somewhere else.
With the usual (and often in different places simplifying) methods, both cases perform almost equally, or show clearly that the total equivalent noise voltage must of course be somewhat lower with the 47k resistor. However, they do not take into account the influence of the voltage divider at the input on the final SNR. The whole trick is the voltage divider, nothing more. If you only look at the noise, the pendulum always swings to the side of the lower impedance termination, never the other way around.
This physical state of affairs cannot please Nick S., even though his EQ is great - the advertising must not now claim that the higher impedance termination leads to less noise.
HBt.
1)
OPu=8e-9
OPi=1.6e-15
G1k=
Rq=12e3
Ltc=
Rdc=
R1=47e3
R2=
R3=
df=
T=27
99.0099 5000000 9559.322 10000 100 12000 47000
3.173164e-008[V] 3.204896e-006[V] 101.888[dB]
1.08458e-006[V] 0.0001095426[V] 71.21266[dB]
short 4.66499e-005[V] 80.60239[dB]
open 4.665196e-005[V] 80.60201[dB]
infinite 4.665004e-005[V] 80.60236[dB] Riq= 12000[Ohm]
reference: 0.3983051[V] 8.726267e-005[V] 73.18774[dB]
reference: 0.3983051[V] 0.000202697[V] 65.86737[dB]
3864.734[V/A] 7.999999811618085e-009[V/sqrt(Hz)]
1.545893761867023e-010[A/V] 1.600000019001911e-015[A/sqrt(Hz)]
124.4740146547698[dB] 6.46875e+009[Ohm]
2)
OPu=8e-9
OPi=1.6e-15
G1k=
Rq=12e3
Ltc=
Rdc=
R1=150e3
R2=
R3=
df=
T=27
99.0099 5000000 11111.11 10000 100 12000 150000
3.687701e-008[V] 3.724578e-006[V] 101.8894[dB]
9.851904e-007[V] 9.950423e-005[V] 73.3541[dB]
short 4.66499e-005[V] 80.60239[dB]
open 4.667089e-005[V] 80.59848[dB]
infinite 4.665004e-005[V] 80.60236[dB] Riq= 12000[Ohm]
reference: 0.462963[V] 9.213348e-005[V] 74.02258[dB]
reference: 0.462963[V] 0.0003147775[V] 63.35085[dB]
3864.734[V/A] 7.999999811618085e-009[V/sqrt(Hz)]
1.545893761867023e-010[A/V] 1.600000019001911e-015[A/sqrt(Hz)]
124.4740146547698[dB] 6.46875e+009[Ohm]
OPu=
C:\Windows\System32>
Nevertheless, a 150kOhm resistor produces more thermal noise than a 47kOhm resistor, the trick is hidden somewhere else.
With the usual (and often in different places simplifying) methods, both cases perform almost equally, or show clearly that the total equivalent noise voltage must of course be somewhat lower with the 47k resistor. However, they do not take into account the influence of the voltage divider at the input on the final SNR. The whole trick is the voltage divider, nothing more. If you only look at the noise, the pendulum always swings to the side of the lower impedance termination, never the other way around.
This physical state of affairs cannot please Nick S., even though his EQ is great - the advertising must not now claim that the higher impedance termination leads to less noise.
HBt.
Erm, no, it generates more voltage noise, but less current noise, and into a matched load all resistances at a given temperature produce the same noise power, otherwise thermodynamics doesn't work!
The circuit topology matters.
My single remaining brain cell isn't up to the task. In Jurassic times, I used the method in one maker's datasheet; the AD one IIRC.
You get curves as a function of frequency with this method.
One caveat is if your display is Log Frequency like Mark's in #9, you should be calculating Constant Relative Bandwidth eg 1/3 8v noise.
Showing V/rt(Hz) like Mark is misleading unless you display with Linear Frequency ... but that's not very useful for audio.
Of course if you just want a single number, both methods should give you the same answer but you might need need to go to 1/12 8ve 😊
The tests were Blind but not Double Blind; once circa 1980 and once early 1990s.
LT1028 was obviously noisier when you lifted the cartridge off the record .. and to some of us playing an LP. Not sure OP27 was available in 1980.
OP27 is like 5534AN but with EVIL input current cancellation so the improvement with 5534 was small but audible when you lifted the cartridge off the record. By 1990, we knew which of our DBLT panel could pick up really small differences. One of them said he could hear the difference playing a clean LP.
It's possible to do DBLTs on preamps but we didn't bother as it was obvious 5534 was at least as good, much cheaper & easily available. 😊
IIRC, we also tested Guru Wurcer's AD 797 in the later test with similar results to LT1028. Scott W said he wasn't surprised when I told him 😲
Du.uh! These days, Constant Relative Bandwidth is always done with a large FFT which dreams up Constant Relative Bandwidth eg 1/3 8v noise.by adding up the FFT bins in the frequency band. So unless your bookkeeping is wonky, today both should give the same single number.
ref #42
Your objection refers to my synonymously used "thermal noise", i.e. the collective term, perhaps remotely comparable with many other everyday phrases or terms - I'll spare myself a long list of examples.
But since you are absolutely correct about the theory of heat - the dynamics, do we now also have to talk about concepts such as pressure, volume, temperature, work, power and internal energy? Or do we just want to briefly interject constancy? Yes. Then we can quickly agree on a constant mean value, on a mean noise-voltage density. All as equal and as equivalent to something unnamed.
U^2 / R
= P_noise, but also = I^2 * R or U * I
(The formula letter U within a size equation corresponds here to Vnoise)
= const
because [k/s] * [Ws/k] is in our case 4 times Temperature times "Boltzmann" times Oscillation - This equation, which I have deliberately disguised, also contains the degrees of freedom, i.e. the possible movement options or even possibilities.
"Boltzmann"
also refers to a certain number of molecules, so somehow we describe the behavior of bodies with temperature changes, ergo m_m times R_s (thermodynamically) is considered constant, provided that the ..!
Dear Mark T.,
don't you agree that we should not continue to describe and invoke the mother of all life, heat, i.e. thermodynamics, here? let us agree, simplifying everything, i.e. relaxing, that "Boltzmann" is regarded as constant.
With the numerical value of 1.38065e-23 times [Nm/k] or also [watt-second per Kelvin], i.e. a work related to the ..!
Since the product UI must now be constant in the case under consideration (the particular oscillation), because "Boltzmann" is constant, this means:
n times U automatically leads to 1/n times I
or vice versa
n times I automatically leads to 1/n times U
So thank you for reminding me of the exactness of the terminology and causal relationships.
greetings,
HBt.
Your objection refers to my synonymously used "thermal noise", i.e. the collective term, perhaps remotely comparable with many other everyday phrases or terms - I'll spare myself a long list of examples.
But since you are absolutely correct about the theory of heat - the dynamics, do we now also have to talk about concepts such as pressure, volume, temperature, work, power and internal energy? Or do we just want to briefly interject constancy? Yes. Then we can quickly agree on a constant mean value, on a mean noise-voltage density. All as equal and as equivalent to something unnamed.
U^2 / R
= P_noise, but also = I^2 * R or U * I
(The formula letter U within a size equation corresponds here to Vnoise)
= const
because [k/s] * [Ws/k] is in our case 4 times Temperature times "Boltzmann" times Oscillation - This equation, which I have deliberately disguised, also contains the degrees of freedom, i.e. the possible movement options or even possibilities.
"Boltzmann"
also refers to a certain number of molecules, so somehow we describe the behavior of bodies with temperature changes, ergo m_m times R_s (thermodynamically) is considered constant, provided that the ..!
Dear Mark T.,
don't you agree that we should not continue to describe and invoke the mother of all life, heat, i.e. thermodynamics, here? let us agree, simplifying everything, i.e. relaxing, that "Boltzmann" is regarded as constant.
With the numerical value of 1.38065e-23 times [Nm/k] or also [watt-second per Kelvin], i.e. a work related to the ..!
Since the product UI must now be constant in the case under consideration (the particular oscillation), because "Boltzmann" is constant, this means:
n times U automatically leads to 1/n times I
or vice versa
n times I automatically leads to 1/n times U
So thank you for reminding me of the exactness of the terminology and causal relationships.
Really, thanks.
Again, this is completely correct - and what next? I mean, your statement alone, without an example, doesn't help any self-builder.
greetings,
HBt.
The little tool is developing, even if it still hasn't progressed beyond calculator status, ...
{
OPu=3e-9
OPi=0.4e-12
99.01 7500 3112.292 10000 100 3333 47000
5.385e-007[V] 5.439e-005[V] 78.674[dB]
4.941e-007[V] 4.99e-005[V] 79.422[dB]
short 1.75e-005[V] 89.121[dB]
open 0.000111[V] 73.072[dB]
infinite 1.914e-005[V] 88.338[dB] Riq= 3333[Ohm]
reference 0.4669[V] 4.656e-005[V] 80.024[dB]
543.222[V/A] 3e-009[V/sqrt(Hz)] 9.657e-006[A/V] 4e-013[A/sqrt(Hz)]
103548.8[Ohm] 2.28
OPu=0.85e-9
OPi=1e-12
99.01 850 3112.292 10000 100 3333 47000
9.912e-008[V] 1.001e-005[V] 93.375[dB]
4.956e-007[V] 5.005e-005[V] 79.396[dB]
short 4.99e-006[V] 100.017[dB]
open 0.0002741[V] 65.221[dB]
infinite 2.007e-005[V] 87.93[dB] Riq= 3333[Ohm]
reference 0.4669[V] 4.651e-005[V] 80.033[dB]
43.609[V/A] 8.5e-010[V/sqrt(Hz)] 6.036e-005[A/V] 1e-012[A/sqrt(Hz)]
16567.8[Ohm] 2.58
OPu=5 e-9
OPi=0.7e-12
99.01 7142.857 3112.292 10000 100 3333 47000
5.217e-007[V] 5.269e-005[V] 78.95[dB]
5.642e-007[V] 5.698e-005[V] 78.27[dB]
short 2.916e-005[V] 84.684[dB]
open 0.0001941[V] 68.221[dB]
infinite 3.218e-005[V] 83.829[dB] Riq= 3333[Ohm]
reference 0.4669[V] 5.311e-005[V] 78.881[dB]
1508.951[V/A] 5e-009[V/sqrt(Hz)] 2.958e-005[A/V] 7e-013[A/sqrt(Hz)]
33811.84[Ohm] 1.35
OPu=8e-9
OPi=1.6e-15
99.01 5000000 3112.292 10000 100 3333 47000
1.661e-005[V] 0.001678[V] 48.89[dB]
6.694e-007[V] 6.761e-005[V] 76.785[dB]
short 4.665e-005[V] 80.602[dB]
open 4.665e-005[V] 80.602[dB]
infinite 4.665e-005[V] 80.602[dB] Riq= 3333[Ohm]
reference 0.4669[V] 6.313e-005[V] 77.38[dB]
3862.915[V/A] 8e-009[V/sqrt(Hz)] 1.545e-010[A/V] 1.6e-015[A/sqrt(Hz)]
6.471797e+009[Ohm] 6.224
OPu=12e-9
OPi=10e-15
99.01 1200000 3112.292 10000 100 3333 47000
8.13e-006[V] 0.0008211[V] 55.096[dB]
8.683e-007[V] 8.77e-005[V] 74.525[dB]
short 6.997e-005[V] 77.081[dB]
open 7.003e-005[V] 77.074[dB]
infinite 6.998e-005[V] 77.081[dB] Riq= 3333[Ohm]
reference 0.4669[V] 8.189e-005[V] 75.12[dB]
8691.559[V/A] 1.2e-008[V/sqrt(Hz)] 6.036e-009[A/V] 1e-014[A/sqrt(Hz)]
1.65678e+008[Ohm] 4.28
OPu=18e-9
OPi=10e-15
99.01 1800000 3112.292 10000 100 3333 47000
9.961e-006[V] 0.001006[V] 53.331[dB]
1.201e-006[V] 0.0001213[V] 71.708[dB]
short 0.000105[V] 73.559[dB]
open 0.000105[V] 73.556[dB]
infinite 0.000105[V] 73.559[dB] Riq= 3333[Ohm]
reference 0.4669[V] 0.0001133[V] 72.303[dB]
19556.01[V/A] 1.8e-008[V/sqrt(Hz)] 6.036e-009[A/V] 1e-014[A/sqrt(Hz)]
1.65678e+008[Ohm] 3.928
OPu=2 0e-9
OPi=0.3e-12
99.01 66666.67 3112.292 10000 100 3333 47000
1.874e-006[V] 0.0001893[V] 67.842[dB]
1.318e-006[V] 0.0001331[V] 70.902[dB]
short 0.0001166[V] 72.644[dB]
open 0.0001427[V] 70.891[dB]
infinite 0.0001168[V] 72.633[dB] Riq= 3333[Ohm]
reference 0.4669[V] 0.0001243[V] 71.498[dB]
24143.22[V/A] 2e-008[V/sqrt(Hz)] 5.432e-006[A/V] 3e-013[A/sqrt(Hz)]
184086.7[Ohm] 0.8822
};
the core algorithm for the calculation has now been established.
Version 1.4
{
OPu=3e-9
OPi=0.4e-12
99.01 7500 3112.292 10000 100 3333 47000
5.385e-007[V] 5.439e-005[V] 78.674[dB]
4.941e-007[V] 4.99e-005[V] 79.422[dB]
short 1.75e-005[V] 89.121[dB]
open 0.000111[V] 73.072[dB]
infinite 1.914e-005[V] 88.338[dB] Riq= 3333[Ohm]
reference 0.4669[V] 4.656e-005[V] 80.024[dB]
543.222[V/A] 3e-009[V/sqrt(Hz)] 9.657e-006[A/V] 4e-013[A/sqrt(Hz)]
103548.8[Ohm] 2.28
OPu=0.85e-9
OPi=1e-12
99.01 850 3112.292 10000 100 3333 47000
9.912e-008[V] 1.001e-005[V] 93.375[dB]
4.956e-007[V] 5.005e-005[V] 79.396[dB]
short 4.99e-006[V] 100.017[dB]
open 0.0002741[V] 65.221[dB]
infinite 2.007e-005[V] 87.93[dB] Riq= 3333[Ohm]
reference 0.4669[V] 4.651e-005[V] 80.033[dB]
43.609[V/A] 8.5e-010[V/sqrt(Hz)] 6.036e-005[A/V] 1e-012[A/sqrt(Hz)]
16567.8[Ohm] 2.58
OPu=5 e-9
OPi=0.7e-12
99.01 7142.857 3112.292 10000 100 3333 47000
5.217e-007[V] 5.269e-005[V] 78.95[dB]
5.642e-007[V] 5.698e-005[V] 78.27[dB]
short 2.916e-005[V] 84.684[dB]
open 0.0001941[V] 68.221[dB]
infinite 3.218e-005[V] 83.829[dB] Riq= 3333[Ohm]
reference 0.4669[V] 5.311e-005[V] 78.881[dB]
1508.951[V/A] 5e-009[V/sqrt(Hz)] 2.958e-005[A/V] 7e-013[A/sqrt(Hz)]
33811.84[Ohm] 1.35
OPu=8e-9
OPi=1.6e-15
99.01 5000000 3112.292 10000 100 3333 47000
1.661e-005[V] 0.001678[V] 48.89[dB]
6.694e-007[V] 6.761e-005[V] 76.785[dB]
short 4.665e-005[V] 80.602[dB]
open 4.665e-005[V] 80.602[dB]
infinite 4.665e-005[V] 80.602[dB] Riq= 3333[Ohm]
reference 0.4669[V] 6.313e-005[V] 77.38[dB]
3862.915[V/A] 8e-009[V/sqrt(Hz)] 1.545e-010[A/V] 1.6e-015[A/sqrt(Hz)]
6.471797e+009[Ohm] 6.224
OPu=12e-9
OPi=10e-15
99.01 1200000 3112.292 10000 100 3333 47000
8.13e-006[V] 0.0008211[V] 55.096[dB]
8.683e-007[V] 8.77e-005[V] 74.525[dB]
short 6.997e-005[V] 77.081[dB]
open 7.003e-005[V] 77.074[dB]
infinite 6.998e-005[V] 77.081[dB] Riq= 3333[Ohm]
reference 0.4669[V] 8.189e-005[V] 75.12[dB]
8691.559[V/A] 1.2e-008[V/sqrt(Hz)] 6.036e-009[A/V] 1e-014[A/sqrt(Hz)]
1.65678e+008[Ohm] 4.28
OPu=18e-9
OPi=10e-15
99.01 1800000 3112.292 10000 100 3333 47000
9.961e-006[V] 0.001006[V] 53.331[dB]
1.201e-006[V] 0.0001213[V] 71.708[dB]
short 0.000105[V] 73.559[dB]
open 0.000105[V] 73.556[dB]
infinite 0.000105[V] 73.559[dB] Riq= 3333[Ohm]
reference 0.4669[V] 0.0001133[V] 72.303[dB]
19556.01[V/A] 1.8e-008[V/sqrt(Hz)] 6.036e-009[A/V] 1e-014[A/sqrt(Hz)]
1.65678e+008[Ohm] 3.928
OPu=2 0e-9
OPi=0.3e-12
99.01 66666.67 3112.292 10000 100 3333 47000
1.874e-006[V] 0.0001893[V] 67.842[dB]
1.318e-006[V] 0.0001331[V] 70.902[dB]
short 0.0001166[V] 72.644[dB]
open 0.0001427[V] 70.891[dB]
infinite 0.0001168[V] 72.633[dB] Riq= 3333[Ohm]
reference 0.4669[V] 0.0001243[V] 71.498[dB]
24143.22[V/A] 2e-008[V/sqrt(Hz)] 5.432e-006[A/V] 3e-013[A/sqrt(Hz)]
184086.7[Ohm] 0.8822
};
the core algorithm for the calculation has now been established.
Version 1.4
Last edited:
From the evaluation of the above list, we can see what we already knew: the LT1028 is the worst possible choice for an MM system, while the OPA627 is the first choice. Unfortunately, under (unfavorable) circumstances, the TL071 could even be preferable to the NE5534.
End of the trip,
HBt.
End of the trip,
HBt.
@kgrlee
is this your calculation-method
you remember? 10 frequency bands, without the influence of the operational amplifier ?
is this your calculation-method
you remember? 10 frequency bands, without the influence of the operational amplifier ?
My last exemplary (repetitive) example for using the small calculator.
For the evaluation, i.e. the assessment of a component suitability (in our case the OP-Amp), all output lines must be consulted. I may describe how to weight and calculate them at a later date.
OPu=8e-9
OPi=1.6e-15
G1k=
Rq=12e3
Ltc=
Rdc=
R1=150e3
R2=
R3=
df=
T=27
99.01 5000000 11111.11 10000 100 12000 150000
1.66e-005[V] 0.001676[V] 48.823[dB]
9.854e-007[V] 9.952e-005[V] 73.353[dB]
short 4.665e-005[V] 80.602[dB]
open 4.667e-005[V] 80.598[dB]
infinite 4.665e-005[V] 80.602[dB] Riq= 12000[Ohm]
reference 0.463[V] 9.215e-005[V] 74.021[dB]
3862.915[V/A] 8e-009[V/sqrt(Hz)] 1.545e-010[A/V] 1.6e-015[A/sqrt(Hz)]
6.471797e+009[Ohm] 6.224
OPu=8e-9
OPi=1.6e-15
G1k=
Rq=12e3
Ltc=
Rdc=
R1=47e3
R2=
R3=
df=
T=27
99.01 5000000 9559.322 10000 100 12000 47000
1.66e-005[V] 0.001677[V] 47.515[dB]
1.085e-006[V] 0.0001096[V] 71.211[dB]
short 4.665e-005[V] 80.602[dB]
open 4.665e-005[V] 80.602[dB]
infinite 4.665e-005[V] 80.602[dB] Riq= 12000[Ohm]
reference 0.3983[V] 8.728e-005[V] 73.186[dB]
3862.915[V/A] 8e-009[V/sqrt(Hz)] 1.545e-010[A/V] 1.6e-015[A/sqrt(Hz)]
6.471797e+009[Ohm] 6.224
The winner in the SNR game is Nick's 150k termination ("passively cooled").
Now it's time for the break,
HBt.
For the evaluation, i.e. the assessment of a component suitability (in our case the OP-Amp), all output lines must be consulted. I may describe how to weight and calculate them at a later date.
OPu=8e-9
OPi=1.6e-15
G1k=
Rq=12e3
Ltc=
Rdc=
R1=150e3
R2=
R3=
df=
T=27
99.01 5000000 11111.11 10000 100 12000 150000
1.66e-005[V] 0.001676[V] 48.823[dB]
9.854e-007[V] 9.952e-005[V] 73.353[dB]
short 4.665e-005[V] 80.602[dB]
open 4.667e-005[V] 80.598[dB]
infinite 4.665e-005[V] 80.602[dB] Riq= 12000[Ohm]
reference 0.463[V] 9.215e-005[V] 74.021[dB]
3862.915[V/A] 8e-009[V/sqrt(Hz)] 1.545e-010[A/V] 1.6e-015[A/sqrt(Hz)]
6.471797e+009[Ohm] 6.224
OPu=8e-9
OPi=1.6e-15
G1k=
Rq=12e3
Ltc=
Rdc=
R1=47e3
R2=
R3=
df=
T=27
99.01 5000000 9559.322 10000 100 12000 47000
1.66e-005[V] 0.001677[V] 47.515[dB]
1.085e-006[V] 0.0001096[V] 71.211[dB]
short 4.665e-005[V] 80.602[dB]
open 4.665e-005[V] 80.602[dB]
infinite 4.665e-005[V] 80.602[dB] Riq= 12000[Ohm]
reference 0.3983[V] 8.728e-005[V] 73.186[dB]
3862.915[V/A] 8e-009[V/sqrt(Hz)] 1.545e-010[A/V] 1.6e-015[A/sqrt(Hz)]
6.471797e+009[Ohm] 6.224
The winner in the SNR game is Nick's 150k termination ("passively cooled").
Now it's time for the break,
HBt.
I think a common issue seen is current noise often being completely ignored, with the assumption that there is only voltage noise.
Understanding that there is current noise (more generally that there is a noise impedance associated with a device), is useful to avoid pitfalls such as thinking a MM cartridge preamp using an AD797 is a good choice.
So I see remarks like "150k noisier than 47k" as examples of this confusion and jump in to clarify that its a bit more complicated than that...
The truth is that sometimes you can ignore current noise, but also sometimes you can ignore voltage noise, and sometimes both matter.
And there's also 1/f noise to worry about too sometimes.
No. The method in the two manufacturer datasheets showed how the cartridge noise, cartridge impedance and the OPA noise interacted. I think the AD OPA was OP27 but the present datasheet doesn't show the calculation of RIAA noise. Still trying to remember who the other maker was.
Checking which of the methods mentioned here is correct should be easy ... unless you have only 1 brain cell like me. OK. I confess. I'm just lazy 😉
Mark, I think it's unfair to say "a common issue seen is current noise often being completely ignored". Loadsa people were aware of this in the early 70s or even 60s eg Radford. Then there are the Marketing VPs who insist on SC noise number 😊
There is no point doing calculations assuming 150k Input Z instead of the 'standard' 47k cos no MM cartridge maker designs their MM cartridges to have flat response with 150k
Last edited:
Thanks for this Jack. Brings back many memories.
We built this on perforated board in a little diecast box when the paper came out and used it for over 2 decades .. even after we had fancier, more $$$ gear. It was so convenient.
So my entry for Single number RIAA noise calculation / simulation is
- First find out the correct method to determine noise in a small frequency band with a reactive sourse ... one of the two mythical manufacturers datasheets I keep rabbiting on about. Wayne Kirkwood and I discussed this some years ago when he was designing his ultimate RIAA preamp. I think he had the correct method and also the 2 datasheets.
- Simulate noise using LTspice to give nV/rt(Hz) in zillion linear frequency bins. Actually I think LTspice can do the above for you too.
- Weight the noise with CCIR-468. Don't do this with a passive filter in LTspice cos that adds extra noise.
- Sum the weighted noise Equivalent to using an RMS meter..
Should work for other stuff like microphone noise too but not impulsive stuff. See Dolby, Robinson et al for detail.
Last edited:
I don't. It's a mistake that has very often been made, also by professionals. I even had to point it out to Douglas Self in the 1990's.
That said, there certainly always have been people who did not make this mistake. Many classical moving-magnet phono amplifiers have a bipolar input transistor biased at a few dozen microamperes, showing that the designers knew exactly what they were doing.
True, but @Nick Sukhov found out that many of them have a pretty good response, actually better than with the specified load, with 150 kohm when you keep the load capacitance very low. A consequence is that the phono amplifier has to be built into the turntable.
Last edited:
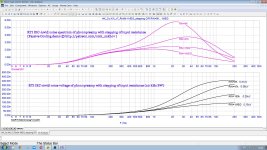
you can do all 4 of your points with one mouse movement in Microcap, with the same reliable result. See my attachment. Replace LTSpice with MC12 [ free here https://www.patreon.com/posts/podstrakhoval-12-84096514 - zip installer only 17 MB ] and you will save a lot of time.
Attachments
Last edited:
By the way:
in the meantime, I have also become a big advocate of MC-12.
Back to OP27, which we find again and again in "B. Vogel, the sound of silence", also on his example calculation "Series Configured Noise Model" pages 88 to 89.
{
OPu=3.2e-9
OPi=0.6e-12
G1k=100
Rq=1e3
Ltc=
Rdc=
R1=47e3
R2=100
R3=
df=20e3
T=20
99.01 5333.333 979.167 10000 100 1000 47000
1.198e-006[V] 0.000121[V] 72.139[dB]
7.657e-007[V] 7.733e-005[V] 76.029[dB]
short 4.572e-005[V] 80.778[dB]
open 0.0004054[V] 61.822[dB]
infinite 4.651e-005[V] 80.628[dB] Riq= 1000[Ohm]
reference 0.4896[V] 7.563e-005[V] 76.223[dB]
632.832[V/A] 3.2e-009[V/sqrt(Hz)] 2.225e-005[A/V] 6e-013[A/sqrt(Hz)]
44947.83[Ohm] 1.851
};
His presented method is the most intuitively plausible, it is hidden (unintentionally, i.e. by chance) in my output line starting with the word "reference". And yet only the third output line captures all noisy sources 100% correctly, according to the doctrine. Doctrinal opinions differ between the leading university institutions and departments. The difference between the method contenders in this OP27 example is 76.223dB-76.029dB=0.194dB.
{
OPu=3.2e-9
OPi=0.6e-12
G1k=100
OPu=3.2e-9
OPi=0.6e-12
G1k=100
Rq=100e3
Ltc=
Rdc=
R1=47e3
R2=
R3=10e3
df=20000
T=20
99.01 5333.333 31972.79 10000 100 100000 47000
4.961e-007[V] 5.01e-005[V] 70.078[dB]
1.327e-005[V] 0.00134[V] 41.534[dB]
short 4.572e-005[V] 80.778[dB]
open 0.0004054[V] 61.822[dB]
infinite 0.0008582[V] 55.307[dB] Riq= 100000[Ohm]
reference 0.1599[V] 0.0004278[V] 51.449[dB]
632.832[V/A] 3.2e-009[V/sqrt(Hz)] 2.225e-005[A/V] 6e-013[A/sqrt(Hz)]
44947.83[Ohm] 1.851
};
On the following pages he compares, among other things, series with shunt fb, but also the influence of the increasing Rq.
His result is |58.905dB|. In the example of the small NoiseCalculator we see immediately that B. Vogel underestimates the influence of the input voltage division, the useful signal. This is why his SNR is 7.456dB better. But unfortunately this is wrong. The 41.534dB of the third output line are correct, I'm sorry to say.
In the "short, open and infinite" lines, we can see what gain is achieved with this trick if you deliberately relate the SNR to a nominal output level that will not actually materialize. The line "infinite" means, there is no R1, or else R1||r_in_OP is infinite.
HBt.
in the meantime, I have also become a big advocate of MC-12.
Back to OP27, which we find again and again in "B. Vogel, the sound of silence", also on his example calculation "Series Configured Noise Model" pages 88 to 89.
{
OPu=3.2e-9
OPi=0.6e-12
G1k=100
Rq=1e3
Ltc=
Rdc=
R1=47e3
R2=100
R3=
df=20e3
T=20
99.01 5333.333 979.167 10000 100 1000 47000
1.198e-006[V] 0.000121[V] 72.139[dB]
7.657e-007[V] 7.733e-005[V] 76.029[dB]
short 4.572e-005[V] 80.778[dB]
open 0.0004054[V] 61.822[dB]
infinite 4.651e-005[V] 80.628[dB] Riq= 1000[Ohm]
reference 0.4896[V] 7.563e-005[V] 76.223[dB]
632.832[V/A] 3.2e-009[V/sqrt(Hz)] 2.225e-005[A/V] 6e-013[A/sqrt(Hz)]
44947.83[Ohm] 1.851
};
His presented method is the most intuitively plausible, it is hidden (unintentionally, i.e. by chance) in my output line starting with the word "reference". And yet only the third output line captures all noisy sources 100% correctly, according to the doctrine. Doctrinal opinions differ between the leading university institutions and departments. The difference between the method contenders in this OP27 example is 76.223dB-76.029dB=0.194dB.
{
OPu=3.2e-9
OPi=0.6e-12
G1k=100
OPu=3.2e-9
OPi=0.6e-12
G1k=100
Rq=100e3
Ltc=
Rdc=
R1=47e3
R2=
R3=10e3
df=20000
T=20
99.01 5333.333 31972.79 10000 100 100000 47000
4.961e-007[V] 5.01e-005[V] 70.078[dB]
1.327e-005[V] 0.00134[V] 41.534[dB]
short 4.572e-005[V] 80.778[dB]
open 0.0004054[V] 61.822[dB]
infinite 0.0008582[V] 55.307[dB] Riq= 100000[Ohm]
reference 0.1599[V] 0.0004278[V] 51.449[dB]
632.832[V/A] 3.2e-009[V/sqrt(Hz)] 2.225e-005[A/V] 6e-013[A/sqrt(Hz)]
44947.83[Ohm] 1.851
};
On the following pages he compares, among other things, series with shunt fb, but also the influence of the increasing Rq.
His result is |58.905dB|. In the example of the small NoiseCalculator we see immediately that B. Vogel underestimates the influence of the input voltage division, the useful signal. This is why his SNR is 7.456dB better. But unfortunately this is wrong. The 41.534dB of the third output line are correct, I'm sorry to say.
In the "short, open and infinite" lines, we can see what gain is achieved with this trick if you deliberately relate the SNR to a nominal output level that will not actually materialize. The line "infinite" means, there is no R1, or else R1||r_in_OP is infinite.
HBt.
Pavel compares ...
Real world measurements with the well-known Shure MM shows no problems with the OP27, and that drives me crazy, because the measurement result should have been worse - considerably worse, also with the LT1028 as deputy of his guild.
The solution to the puzzle can only be:
Rq increases with frequency, while jOmegaLtc decreases, i.e. with all the nice measurements (which are not wrong!) the influence of the complex signal source impedance (on the heard result) remains uncovered. And Richard L. will have recognized this on his countless dives.
kindly,
HBt.
Real world measurements with the well-known Shure MM shows no problems with the OP27, and that drives me crazy, because the measurement result should have been worse - considerably worse, also with the LT1028 as deputy of his guild.
The solution to the puzzle can only be:
Rq increases with frequency, while jOmegaLtc decreases, i.e. with all the nice measurements (which are not wrong!) the influence of the complex signal source impedance (on the heard result) remains uncovered. And Richard L. will have recognized this on his countless dives.
kindly,
HBt.
"short 4.572e-005[V] 80.778[dB]" [noise_1_4.exe]
This is the limit, a limit that we will never reach, let alone see, in real-life practice.
"632.832[V/A] 3.2e-009[V/sqrt(Hz)] 2.225e-005[A/V] 6e-013[A/sqrt(Hz)] 44947.83[Ohm] 1.851" [noise_1_4.exe]
This line refers directly to the component, in this case the OP27. For jFet inputs and MM usability (large DC coil resistance, with similarly large inductance), the last floating point numerical value should be at least greater than 4.
This is the limit, a limit that we will never reach, let alone see, in real-life practice.
"632.832[V/A] 3.2e-009[V/sqrt(Hz)] 2.225e-005[A/V] 6e-013[A/sqrt(Hz)] 44947.83[Ohm] 1.851" [noise_1_4.exe]
This line refers directly to the component, in this case the OP27. For jFet inputs and MM usability (large DC coil resistance, with similarly large inductance), the last floating point numerical value should be at least greater than 4.
Apparently there are several brands of OP27 and there are performance differences between them.
Looking at the TI datasheet,
https://www.ti.com/lit/ds/symlink/op27.pdf
you see an internal schematic that is full of obvious mistakes, such as three transistors of the wrong polarity and both sides of the second stage differential pair being connected to the same output of the input stage, but ignoring those, you see that the base current compensation circuit works on a scaled-down version of the input stage tail current (120 uA versus 240uA). You can therefore expect a substantial common-mode component of the input noise current.
Figure 27 shows a noise measurement circuit that cancels the common-mode component of the input noise current, leading to unrealistically good values. Even with this trick in place, the table on page 5 specifies a typical equivalent input noise current of 0.7 pA/√Hz at 1 kHz.
Looking at the Analog Devices datasheet, https://www.analog.com/media/en/technical-documentation/data-sheets/OP27.pdf , the equivalent input noise current is specified as 0.4 pA/√Hz on page 4. Whether this is under realistic or unrealistic conditions is unclear.
Looking at the TI datasheet,
https://www.ti.com/lit/ds/symlink/op27.pdf
you see an internal schematic that is full of obvious mistakes, such as three transistors of the wrong polarity and both sides of the second stage differential pair being connected to the same output of the input stage, but ignoring those, you see that the base current compensation circuit works on a scaled-down version of the input stage tail current (120 uA versus 240uA). You can therefore expect a substantial common-mode component of the input noise current.
Figure 27 shows a noise measurement circuit that cancels the common-mode component of the input noise current, leading to unrealistically good values. Even with this trick in place, the table on page 5 specifies a typical equivalent input noise current of 0.7 pA/√Hz at 1 kHz.
Looking at the Analog Devices datasheet, https://www.analog.com/media/en/technical-documentation/data-sheets/OP27.pdf , the equivalent input noise current is specified as 0.4 pA/√Hz on page 4. Whether this is under realistic or unrealistic conditions is unclear.
Last edited: