Source of that info can be found where?
Probably, meaning that there is a chance you can? Wow, so much generosity with self credit. 😱
I never stated such. Please attribute only what I have said to me.
I do not recall you providing any dialogue on what happens to the resultant output if one of the sidebands is truncated by a steep filter...
Again...
I never stated such. Please attribute only what I have said to me.
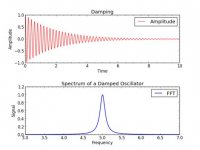
From my previous example, I looked for and found this: the spectra of a damped sinusoid.
Note the spread of the spectrum around the fundamental.
If this is scaled to 20 khz for example, the energy heads out to 22K. If the decay is faster, the spread is more.
Odd, this is apparently bog standard MRI stuff.
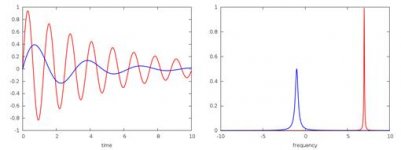
Second pic shows two, the blue damped faster. Note the spectra is wider. The text associated with that find mentioned that.
jn
Attachments
Last edited:
Not sure this would make any sense however I would try. AM modulation x two tone summation.
Attachments
Last edited:
Did someone mention trigonometry? 😉 Also check the section on phase and group velocity Envelope (waves - Wikipedia)
Nice pics.
Note that the AM modulation envelope you present is entirely different. Every single lobe is exactly the same, whereas a true 100% modulation flips phase of the carrier every lobe.
I see a large deadband between envelopes. When a line is fit to the tips of the carrier, as it goes through zero, it must continue through to the bottom of the next lobe. That yours doesn't means you changed the modulation away from a true cosine modulation.
How long did it take you to modify the results until it matched what you wanted to say?
Please modulate using a true function which reverses sign every lobe.
Nice try though.
Edit. I retain exactly what I said above for clarity.
PMA, I apologize. I have found instances of both on the web, so retract my statement that you were in essence being nefarious.
That said, in both cases, a sideband exists that is above filter cutoff, so you still prove that there is content above the cutoff, which when removed, leaves sonething that is not the same as the original.
jn
Last edited:
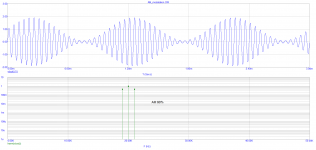
I do not know what you mean. Maybe 2 minutes. This was a 100% AM. AM 90% looks like attached. You talk and think maybe to much, John.
P.S.: modulated by sine, in both cases.
Attachments
AHA, the distinction. PMA is modulation with the envelope varying from zero to peak, in other words a sine that is offset so it never crosses zero. That always preserves the carrier as there is no flip in sign of the envelope.
The math of two sines in beat is exactly the same as amplitude modulation where the envelope passes through zero and is symmetric to it. As a result, half of the carrier is 180 degrees out of phase, and the resultant FFT show no carrier..
In both cases however, the sidebands are still there.
jn
The math of two sines in beat is exactly the same as amplitude modulation where the envelope passes through zero and is symmetric to it. As a result, half of the carrier is 180 degrees out of phase, and the resultant FFT show no carrier..
In both cases however, the sidebands are still there.
jn
Jn, you are still confusing beating (interference) with modulation. Also as far as I'm aware no one has said modulation doesn't produce sidebands.
No, I am not.
But I did figure out why the carrier is in one and not the other.
But the carrier's presence has nothing to do the discussion, as it's the upper sideband that is the concern.
jn
Why, the product of 17.5k and 22.5k has no 17.5k in its spectrum? You can't apply the concept of filtering to the product of two waveforms until after you compute the spectrum of the product.
Who said anything about the product of 17.5 and 22.5?
It's the product of a sine at 2.5k times a sine at 20K, and that is equal to the sum of 17.5 and 22.5.
Your question confuses.
jn
why? that has nothing to do with the discussion of envelope modulation of a primary frequency creating sidebands.
jn
Modulation and simple summation are two absolutely different processes. You still seem not to take it into account. The similarity of time domain waveforms is not any proof of the process sameness. You seem to try to hold some strange integrity of your initial false assumption that two tone summation is an AM modulation.
Don't know.
I started this mess to explain how changing the amplitude of a high frequency sine at a high rate will cause sidebands that could exceed nyquist. I also said that removal of the upper sideband by a brick filter will be removing information that is needed to correctly reproduce the input.
I gave a sine modulation of 20K as an example. I refer to sine modulation of a signal as multiplying the signal by a sine which varies from -1 to +1.
And that modulation type is exactly equivalent to the addition of two sines.
Pavel's example made me realize that he is modulating with a sine that goes from zero to 1, so does not flip the carrier.
My modulation removes the carrier from the fft because it flips the sign of the signal every lobe while zero to +1 does not, hence the carrier in Pavel's example, none in mine.
The fact remains, amplitude modulation (as in music content) will produce sidebands. I suspect those who apparently hear a difference may be sensitive to that. I am not.
jn
See now this has just gone round and round. Same argument, the product of 20k and 2.5k has neither in its spectrum
Modulation from zero to 1 is different, I agree.
Modulation with a cosine is identical.
I at the very beginning pointed out the flip of carrier in the identical waveforms.
Process sameness? Really? The time domain waveforms I provided are absolutely exact. Remember, it is the cos envelope that flips sign. You must understand that distinction.
And, you are simply diverting from the primary discussion of music having envelope modulation that creates sidebands.
jn
- Status
- Not open for further replies.