Marcel,
Two filters in series, the second one working at twice the speed, but both having the same set of coefficients that Hayk used now.
When leaving a section signal rings at Fs/2, true ?
So the first section will ring at 22.05khz and the second at 44.1Khz.
How could this result in a combined ringing only at 22.05Khz ?
Hans
Because there is nothing exciting the second filter's ringing.
At the output of the first filter, you have a signal band from 0 to 22.05 kHz, from 66.15 kHz to 110.25 kHz and copies every 88.2 kHz. How is that going to excite ringing at or just above 44.1 kHz?
At the output of the first filter, you have a signal band from 0 to 22.05 kHz, from 66.15 kHz to 110.25 kHz and copies every 88.2 kHz. How is that going to excite ringing at or just above 44.1 kHz?
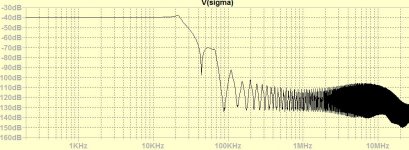
Giving extra gain of 0.45% to midpoints, the 24khz image vanishes.
I am now looking to interpolate the sinc looking only the 30 succeeding samples to avoid pre ringing.
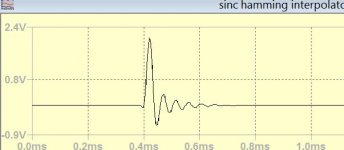
I am now looking to interpolate the sinc looking only the 30 succeeding samples to avoid pre ringing.
When interpolating three points in parallel instead of one at Fs, three polyphase filters are needed.
But when using only one and placing a second identical segment working at 2Fs behind the first, there are only two filters in action.
You might be true, but I have a problem understanding how these two versions can produce the same result with only 2/3 of the amount of multiplications.
Hans
P.s. But at the end the result is in both cases that there are three interpolated points.
So your thesis can’t be that far off. Funny problem.
Last edited:
Not counting the trivial filters that only delay the signal by an integer number of samples, you indeed need three versus two filters, but when the second filter in the cascade has to work at twice the speed, the number of multiplications stays roughly constant. You could get away with a shorter filter for the second stage by giving it a larger transition band, then you do reduce the required number of multiplications.
Interpolation by large factors is usually done with a chain of interpolating filters, the filters getting simpler and simpler as you go further down the chain. The last couple of stages are often CIC filters, which just have adders, subtractors and registers and no multipliers at all.
Marcel,
Yes, with two filters in series, the second filter has to produce two interpolations versus only one for the first filter.
So in effect three convolutions have to be calculated in series between two original samples, exactly the same as with three parallel filters.
So the amount of multiplications is the same in both cases, par. or serie. 😀
Hans
Nice trick to make filters simpler down the chain.
Yes, with two filters in series, the second filter has to produce two interpolations versus only one for the first filter.
So in effect three convolutions have to be calculated in series between two original samples, exactly the same as with three parallel filters.
So the amount of multiplications is the same in both cases, par. or serie. 😀
Hans
Nice trick to make filters simpler down the chain.
Last edited:
Modified sinc interpolator
I found an alternative sinc interpolation that doesn't have ringings.
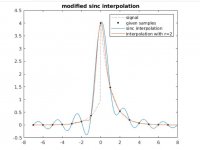
The formula is too complicated for me to understand.
Interpolation: Find good approximation from given samples
I will try to decipher by trial and error, or may be my son (PhD), too busy, can do it.
I found an alternative sinc interpolation that doesn't have ringings.
The formula is too complicated for me to understand.
Interpolation: Find good approximation from given samples
I will try to decipher by trial and error, or may be my son (PhD), too busy, can do it.
Interesting, never seen this before in a DAC.
Let your son pay attention, I'll do the same.
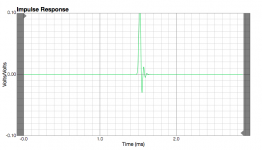
Anxious to see what the FFT of this impulse response will show.
Hans
Let your son pay attention, I'll do the same.
Anxious to see what the FFT of this impulse response will show.
Hans
I understood the formula. The second term sinc delta square is the type of function as the Hamming window. The delta can be between 0 and h-¹/2. the (sinc(pi)2t/h)² is 1.414/(pi*nh)² nh=0.5 to 14.5 this value falls rapidly from 0.81 for the first to 0.03 for the third sample. In other words it reduces considerably the precision of the interpolation, as it relies mainly on few samples. I am happy at least I learned what is Dirac delta function.
There is another way of reducing the ringing used in biomedical imagery by Yaroslavski,
There is another way of reducing the ringing used in biomedical imagery by Yaroslavski,
Last edited:
Hayk,
You could use this free filter sotware tool, to produce all kind of linear phase, minimum phase or whatever type of filter.
rePhase - Official Site - Free FIR filtering tool
Also look here where they managed to create a minimum phase filter with no pre ringing and nearly only one post wave, by stacking mininum phase filters with a distance of 2Khz.
Filter brewing for the Soekris R2R
Hans
.
You could use this free filter sotware tool, to produce all kind of linear phase, minimum phase or whatever type of filter.
rePhase - Official Site - Free FIR filtering tool
Also look here where they managed to create a minimum phase filter with no pre ringing and nearly only one post wave, by stacking mininum phase filters with a distance of 2Khz.
Filter brewing for the Soekris R2R
Hans
.
Attachments
You should ask them for the details how they managed to use rePhase in combination with other programs to get this impulse response.
Hans
Hans
I could make very easily non pre ringing interpolator, the image rejection is a disaster.
t
The frequency response of the impulse you show is ridiculous as mine, -25db at 30khz.
tThe frequency response of the impulse you show is ridiculous as mine, -25db at 30khz.
Last edited:
The rephase software I have it downloaded in early January, brickwall linearphase 21khz, needs 16k samples,
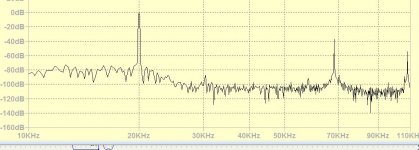
True, but this was also the case with the T+A DAC test that I showed a number of postings ago #367.
But nevertheless, the reviewer preferred this filter.
So it’s a brickwall and somewhat cooler sound or a friendlier rol off of a minimal phase filter and “better” sound.
Hans
A Blackman Harris window also looks attractive to use when playing with rePhase.
Very smooth with a large stopband supression.
Hans
Very smooth with a large stopband supression.
Hans
I have several of those nos USB stick soundcards that cost a $ or two. They all have harsh sound, I use to transform the Laptop into generator/scope.
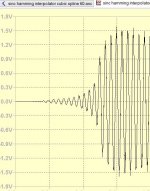
I will study a more important aspect than the ringing, The transient 20khz. It needs three cycles to reach the steady state. I will see what I get with 60 samples.
The arrow shows the start of 20khz.
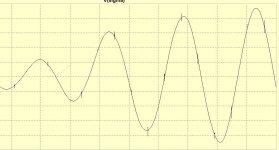
I will study a more important aspect than the ringing, The transient 20khz. It needs three cycles to reach the steady state. I will see what I get with 60 samples.
The arrow shows the start of 20khz.
More samples means more pre and post ring cycles.
Maybe you can try the added N+1 and N-1 trick to reduce ring cycles.
Hans
Maybe you can try the added N+1 and N-1 trick to reduce ring cycles.
Hans
