Acoustic Horn Design – The Easy Way (Ath4)

Jump to Latest
#16,123
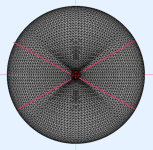
I have a follow-up question from yesterday: The asymmetric profile is generated with the use of x*sin(p)^2. So all manipulation is changing with the angle. This does work to some extend, but for a more proper design, I would need to extend the vertical manipulation further, thus somewhat giving a higher weighting to the middle angles between 0 and 90 degree. Is there currently a way in ath how I can define this? Here is an illustration of what I mean:


wg4.png wg2(1).png wg3(1).png

sheeple said:
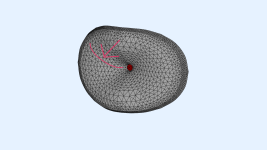
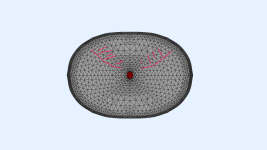
Code: 
R-OSSE = {
  R = 160     - 50*sin(p)^2
  r0 = 8
  a0 = 10.85
  a = 60     -18*sin(p)^2
  k = 0.4     + 2.5*sin(p)^2
  r = 0.18     - 0.07*cos(p)^2 + 0.05*sin(p)^2
  b = 1.2     + 0.2*cos(p)^2 - 0.8*sin(p)^2
  m = 0.8
  q = 5 + 1*cos(p)^2 + 3*sin(p)^2
}
Click to expand...
 
Last edited:
#16,124
If the possbility of changing anything with angle is not enough for you, I'm afraid it's all that can be done. But you can use expressions more complex than the most simple ones you use currently - you can change the period(s), use higher exponents for sin(), add more different terms, etc. If you were tireless enough, you could build something like a FFT series for basically anything (adding up different sines along the circumference, the same way as harmonics add in a signal). Desmos is a great tool for this.

Also, by using functions like floor() I believe it's possible to add even a simple logic to the expressions ("if angle > X then ...").

https://at-horns.eu/release/Ath-4.8.2-UserGuide.pdf#page=63

I'd try to work more with a0 in combination with k perhaps on the vertical. You really don't want a to be less than a0 anywhere...
 
Last edited:
  • Like
Reactions: tmuikku
#16,128
sheeple said:
What do you mean by that?
Click to expand...
That it's not good to have wall slope decreasing anywhere. From your pictures I'd say that you want to decrease a0, a and increase k in the vertical. In how narrow angle interval is controlled by the sine exponent (2, 4, 6, ...). And perhaps something else as well but cut&try is all there is at the moment.

But I suspect you would be dissapointed with the performance.
 
#16,137
Symmetric face!🙂 In addition you might be able to add slight "diffraction slot", IOW start horizontal wideing of the profile bit further from the throat than the vertical. Consider similar sine function to the throat extension, if you wish to make even more asymmetric nominal coverage pattern. I don't know how would it work, probably just some more math 🙂
 
#16,139
You can easily try it: https://at-horns.eu/ext/ath-2024-11a.zip

There are two new weighting functions for this:

trwu(p0, p1, n, p) ... transition from 0 to 1 at the interval <p0, p1>
trwd(p0, p1, n, p) ... transition from 1 to 0 at the interval <p0, p1>

The angles p0 and p1 are in radians (= deg * pi/180).
To apply a modifier with the transition starting at 30 deg (=0.5236 rad) it would be e.g.: trwu(0.5236, 0.8, 2, p)

The parameter n controls the shape of the transition (see an example).

1730534533397.png
 
Last edited:
  • Like
Reactions: Naturlyd, Eggg3r and vineethkumar01
You must log in or register to reply here.
Top Bottom