Cartridge dynamic behaviour

[scott wurcer]

So long as f doesn't change too much in each timeslice, FFT of each timeslice will report amplitude for integration by summing over a certain bandwidth, and either FFT or HT can deliver the mean f. The bandwidth might need to be carefully chosen or adaptive, but I think each timeslice contains equal energy modified only by rpm which is a restatement of mean f. So I really think all the elements are there...………………


LD

I could try that, the HT might not be necessary with a slow sweep. All the energy would still fall in one bin. In fact there are some nice flat-top weighting functions that might work very well.

 

[luckythedog]

All the energy would still fall in one bin. In fact there are some nice flat-top weighting functions that might work very well.

Or across a few bins if we choose, according to sample rate. That allows for quite accurate determination of f, as well as amplitude, from one FFT of a timeslice.

LD

 

[billshurv]

Dumb question, would this also help with doing relative friction measurements?

 

[luckythedog]

Or across a few bins if we choose, according to sample rate. That allows for quite accurate determination of f, as well as amplitude, from one FFT of a timeslice.

LD

Also, there's no reason all timeslices/points in an f sweep need be plotted in the overall result. This might help avoid pop/crackle noise artefacts because noisy timeslices can be discarded based a wideband noise threshold from the same FFT?

LD

 

[luckythedog]

Dumb question, would this also help with doing relative friction measurements?

Yes - rate of change of f sweep so arising will depend on drag, from say, slipping the belt.

Reminds me, I have a late 1950's Lenco transcription table in storage, which has varispeed to 80+ rpm and can disengage the drive...…………

LD

 

[Hans Polak]

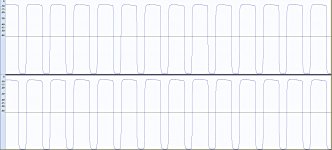
Fresh from the needle the first unfiltered test from the Ortofon record, a square wave.
Looks very nice and clean.
Still working on a 60dB flat amp for the CV sweep.


Hans

 

[Hans Polak]

And this is the same signal but now over a period of 28sec and again completely unfiltered
No clicks, no pops, I have never seen such a clean signal !


Hans

 

[scott wurcer]

Fresh from the needle the first unfiltered test from the Ortofon record, a square wave.
Looks very nice and clean.
Still working on a 60dB flat amp for the CV sweep.


Hans

Is the duty cycle really that far away from 50%?

 

[JP]

I ordered one too but am now leaving for the house tonight so I won't get to play with it until next weekend.

 

[luckythedog]

Is the duty cycle really that far away from 50%?

It's intentional 7:3 duty cycle 400Hz. I wonder why?

Rise times and corners look asymmetric and v soft at first sight........

LD

 

[ThomasA]

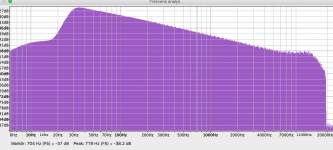
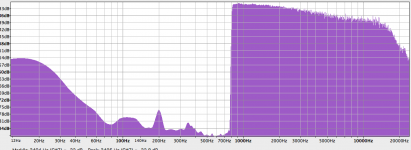
If I compare an FFT of the 30 Hz to 18 kHz sweep on the Elipson, I can see that the slope is 3 dB/octave up to 10 kHz, then the peaking of the resonant stylus shows up. With the Ortofon, I made an electronic compensation for the RIAA and I can see that the response is not at all the same. It has a rising response from 800 Hz to 2-3 kHz.

If I get time I can make the conversion to linear to compare them side by side.

 

[scott wurcer]

It's intentional 7:3 duty cycle 400Hz. I wonder why?

Rise times and corners look asymmetric and v soft at first sight........

LD

The only square wave tracks I have are no RIAA, I would think the pre-emphasis would be problematic while applying a square wave directly to the cutter makes sense. This way the acceleration numbers are easy to compute as you have shown.

 

[Hans Polak]

If I compare an FFT of the 30 Hz to 18 kHz sweep on the Elipson, I can see that the slope is 3 dB/octave up to 10 kHz, then the peaking of the resonant stylus shows up. With the Ortofon, I made an electronic compensation for the RIAA and I can see that the response is not at all the same. It has a rising response from 800 Hz to 2-3 kHz.

If I get time I can make the conversion to linear to compare them side by side.

Hi Thomas,
With the Ortofon you have to play through a straight, non Riaa preamp.


Hans

 

[ThomasA]

Hi Thomas,
With the Ortofon you have to play through a straight, non Riaa preamp.


Hans

Yes. I made however a inverse RIAA electronically in this case.

 

[Hans Polak]

It's intentional 7:3 duty cycle 400Hz. I wonder why?

Rise times and corners look asymmetric and v soft at first sight........

LD

Tomorrow I will do the same with a straight amp, there is no advice on the record what should be done.
This will of course change the shape considerably.

Hans

 

[Hans Polak]

I ordered one too but am now leaving for the house tonight so I won't get to play with it until next weekend.

That's great that you have one on order.
We can compare results and try to agree on some sort of validated transfer curve.


Hans

 

[Hans Polak]

Yes. I made however a inverse RIAA electronically in this case.

That's very strange. Are you sure the correction actually took place ?


Hans

 

[ThomasA]

That's very strange. Are you sure the correction actually took place ?


Hans

Below two pics of before and after correction.

 

[ThomasA]

One good thing with the Ortofon is the very low crosstalk numbers for the 1 kHz test signals. I've got no test record with so low numbers. There is a possibility that the cutter is responsible for this, if they use an Ortofon cutter. See Josh pages in link:

VTA

 

[luckythedog]

Tomorrow I will do the same with a straight amp

No surprise then. That is meant to be played with flat eq 🙄 Otherwise looks heavily rolled off...…..

LD