The original problem was solved way back, bucks bunny, i.e. the entire area in red is 21 point whatever.
Cal then set us to calculating the individual red areas, which proved challenging when it came to the two smaller red areas at bottom left and top right.
EDIT: However your solution to the original problem is elegant!
Cal then set us to calculating the individual red areas, which proved challenging when it came to the two smaller red areas at bottom left and top right.
EDIT: However your solution to the original problem is elegant!
Last edited:
There is a solution. However I had some help in knowing that so I won't spoil it, but I will say that if I drew one line on the diagram it might set the train in motion.I suspect there is no algebraic solution.
Yes, just those two pesky sections that I am yet to understand how to calculate. I might have known at one time but with the steady decline in active brain cells, I feel I might have left it too long. 🙂
For the section in the upper right, I have a feeling that line would be drawn from the upper right corner down to the low point of the first circle on the right creating an ability to measure that little section in the middle between the lines. Just don't know how to do it.but I will say that if I drew one line on the diagram it might set the train in motion.
I think we can ALL AGREE the original problem has been solved!
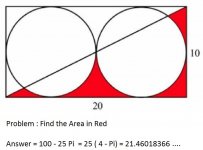
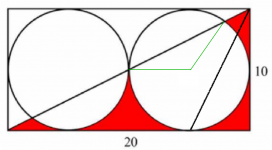
Calculate the Red Area.
25 (4 - Pi) or 100 - 25Pi. 21.46018366...
For some reason some people have tried to solve a more difficult problem. 😕
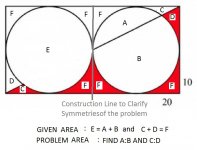
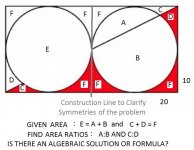
Monsieur mcchambin, with all respect, has failed to satisfy me with his solution to the problem I state below in a multilingual picture. I persist that there is no exact algebraic solution. Since the Transcendentals outnumber the Algebraics by Infinity, I am confident in my chances here.
But am frequently wrong. 😱
Could AllenB be the dark horse that upsets all our calculations with his single drawn line? I await with interest.
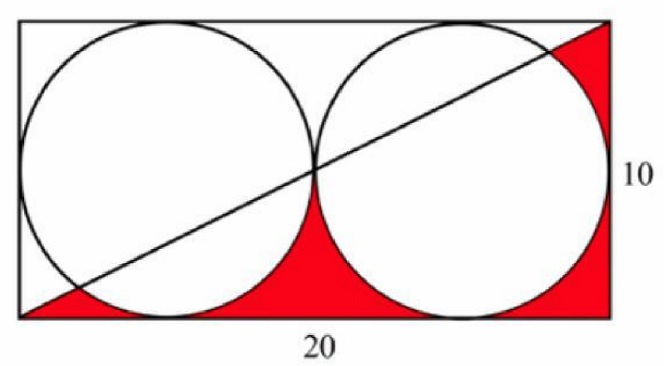
Calculate the Red Area.
25 (4 - Pi) or 100 - 25Pi. 21.46018366...

For some reason some people have tried to solve a more difficult problem. 😕
Monsieur mcchambin, with all respect, has failed to satisfy me with his solution to the problem I state below in a multilingual picture. I persist that there is no exact algebraic solution. Since the Transcendentals outnumber the Algebraics by Infinity, I am confident in my chances here.
But am frequently wrong. 😱
Could AllenB be the dark horse that upsets all our calculations with his single drawn line? I await with interest.
Attachments
To better illustrate, I think this might be the line. The part I can no longer do is the arc on the bottom of the small triangle created by the new line. That's all we'd need to figure it out including the area of the lower left.
Allen?
Allen?
Attachments
...part two is to find the area of each of the red pieces.
You are late to this problem, Steve!For some reason some people have tried to solve a more difficult problem. 😕
As you can see, Cal set us PART 2 of the problem, which mchambin has solved and to which he and I have contributed the method of solution!
Maybe lets stay away from stories about spilled beer. Maybe finding free beer at the store would be better.
What is it you don't understand?Tired of these hard math problems? Making your brain go numb?
I and mchambin have solved part 2 of the problem!
My brain is numbed by the endless recycling of what's already been solved!
Our shapes were congruent 🙂See? ..🙂
What would a Vulcanian have in his quarters besides a computer..
Attachments
snip...I and mchambin have solved part 2 of the problem!
---snip
A Claim that can only be justified by exact references and peer-review, IMO.
So far you are looking a bit Woolly. 😱
Mathematics is an exact discipline! We don't build the future on wobbly foundations. Will the future inhabitants of Planet Earth refer to the Galu-mcchambin Theorem just like they will to Pythoagoras' Theorem? Enquiring minds want to know. 🙂
It's either right, or it isn't. Sorry to rant.
Attachments
I understand that members want to work this out for themselves.
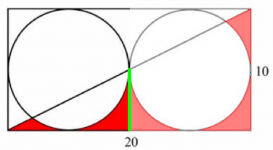
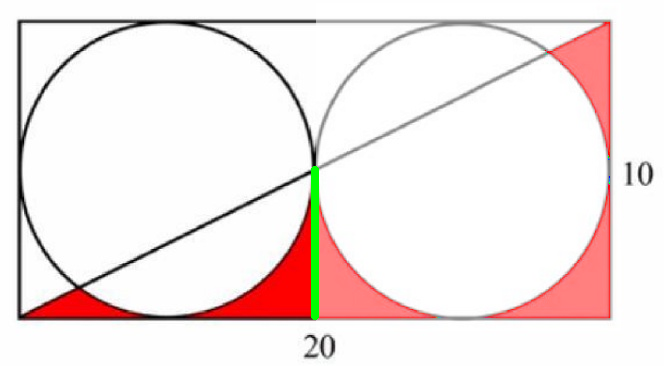
Allen's diagram in post #1186 shows what I described in words.
Looking at the bottom left triangle (to the left of the vertical green line), we see that its area is made up of three parts.
Find the area of the middle part.
Allen's diagram in post #1186 shows what I described in words.
Looking at the bottom left triangle (to the left of the vertical green line), we see that its area is made up of three parts.
Find the area of the middle part.
Below is Cal's First Problem. We can mark that solved.
Cal's Second Problem is also below in an equivalent form:
I think we are all up to speed on this now. And I looked at AllenB's construction in #1186.
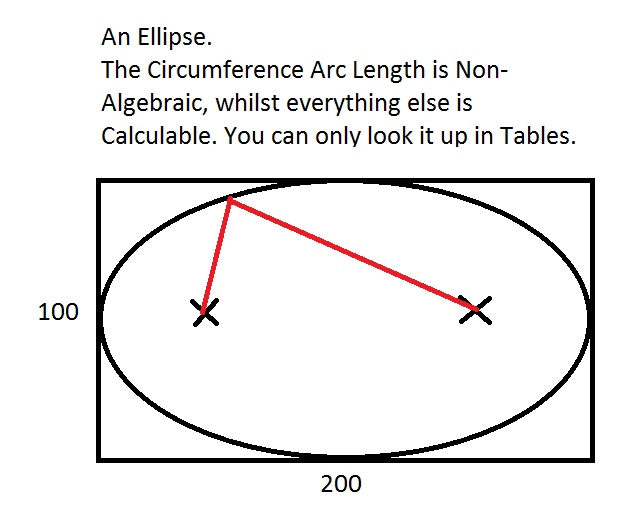
But how does it help? I am still thinking this is an ellipse problem with no exact solution. 😕
All this talk of isosceles triangles and (approximation) to 30 degrees and sines and arctans isn't lighting me up. No light bulb is coming on. I don't get it. 😀
Cal's Second Problem is also below in an equivalent form:
Okay, I have my answer.
EDIT: I checked with Presh Talwaker and was right but part two is to find the area of each of the red pieces.
I think we are all up to speed on this now. And I looked at AllenB's construction in #1186.
But how does it help? I am still thinking this is an ellipse problem with no exact solution. 😕
All this talk of isosceles triangles and (approximation) to 30 degrees and sines and arctans isn't lighting me up. No light bulb is coming on. I don't get it. 😀
Attachments
Maybe lets stay away from stories about spilled beer. Maybe finding free beer at the store would be better.
Tramp #1: Why is your tongue black?
Tramp #2: Dropped a bottle of wiskey?
Tramp #1: That bad, but why did make your tongue black?
Tramp #2: Had to lick it up and the tarmac was newly laid ...
To better illustrate, I think this might be the line.
this is just flipping the existing line through a 45°-diagonal. so no new line and no solution ...
do i spoil everything with my green lines?

Attachments
Last edited:
- Home
- Member Areas
- The Lounge
- Something to lighten the mood