Okay, I have my answer.
EDIT: I checked with Presh Talwaker and was right but part two is to find the area of each of the red pieces.
EDIT: I checked with Presh Talwaker and was right but part two is to find the area of each of the red pieces.
Attachments
Hint: Area of quadrants.Okay, I have my answer.
EDIT: I checked with Presh Talwaker and was right but part two is to find the area of each of the red pieces.
Yes, I'll have a go in a bit. Two of the 4 look easy.
Edit: Yes, simple arithmetic. Those other two irregular shaped ones might be beyond my ability. I know what their combined size is 😀
Edit: Yes, simple arithmetic. Those other two irregular shaped ones might be beyond my ability. I know what their combined size is 😀
Last edited:
The tricky bit is the red area on bottom left!
or the one on top right ... 😀
Last edited:
Nice approach.see image - it was great fun, thanks! 😎
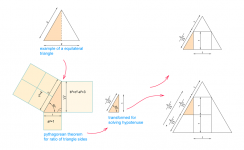
You start with cube edge =1 then go at finding triangle edge.
I did the other way starting with triangle edge=1.
I used the trick of the isocele triangle seen in the previous puzzle ( the puzzle asking for the angle that happened to be 120°). Because of the 15° angle of the isocele triangle, it's complement happens to come in tan(75°).
So I found simple formulas but containing a not so nice tan() term.
Then matching your formulas with mines, I discovered that tan(75°) is 2 + sqrt(3).
Then I reworked my formulas that became quite simple, but written different than yours.
Now, new mind bender:
Prouve tan(75°) = 2 + sqrt(3)
Did you hear about the mathematician who’s afraid of negative numbers?
He’ll stop at nothing to avoid them.
He’ll stop at nothing to avoid them.
I once asked a German student, "Do you know the square root of 81?".Prouve tan(75°) = 2 + sqrt(3)
He didn't seem to know, no matter how many times I asked him. 😉
He didn't seem to know, no matter how many times I asked him. 😉
😕
😕
...
😀
It is the same, yes?see image
Attachments
I need to revise my geometry.
Attachments
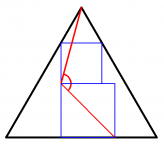
About puzzle in post #1120
Two circles in a rectangle.
I think I found a way for the top right red area.
triangle area - ( half circle area - segment area )
Giving
5² - Pi.5²/2 + Segment area
Segment angle is: a = 180° - 2*atan(0.5)
Segment area = ( a* Pi/360 - sin(a)/2)*5²
This is too horrible, I give up.
Two circles in a rectangle.
I think I found a way for the top right red area.
triangle area - ( half circle area - segment area )
Giving
5² - Pi.5²/2 + Segment area
Segment angle is: a = 180° - 2*atan(0.5)
Segment area = ( a* Pi/360 - sin(a)/2)*5²
This is too horrible, I give up.
Last edited:
- Home
- Member Areas
- The Lounge
- Something to lighten the mood