I am hoping that Cal sets us a hard one next. I have solved the Riemann Hypothesis, an unexpected solution, but this page is too small to contain it. 😉
Quanta Magazine
Quanta Magazine
Cal wants to lighten the mood, not discourage. I can assure you if we see him again soon he will bring forth an offering that allows many of the members to participate. Exclusivity not permitted.
A graphic solution is easy, but I guess you want some equation.
Looks like 4 Pi.
Edit: Prooved 🙂
Looks like 4 Pi.
Edit: Prooved 🙂
Last edited:
I apologize for this. When mountain hiking i should solve puzzles without posting images from my mobile 😱
I think it might be (324/49)*pi. I will check when at home!
Last edited:
The proof is missing at this link, it just gives a cook book result.
This is for cheaters who do not want to understand a thing.
Thanks to internet we are well on the way to Idiocracy. Idiocracy, the movie.
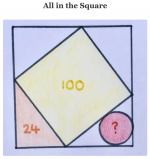
If you calculate the sides of the four triangles, it will be easy. Pythagoras' theorem a^2 + b^2 = c^2, here c = 10 and a x b = 24, then a = 6 and b = 8. Proof: 36 + 64 = 100, and (6 x 8) / 2 = 24. You can use some math to get to this result.
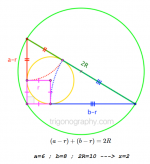
Now we calculate the radius of the circle. Draw three radii with length r, two of them is perpendicular to the sides of the triangle, one is perpendicular to the hypotenuse (that is the side of the inner rectangle). (a - r) + (b -r) = 10 the length of the hypotenuse. From this equation r = 2. The area is r^2 x Pi = 4 x Pi.
Now we calculate the radius of the circle. Draw three radii with length r, two of them is perpendicular to the sides of the triangle, one is perpendicular to the hypotenuse (that is the side of the inner rectangle). (a - r) + (b -r) = 10 the length of the hypotenuse. From this equation r = 2. The area is r^2 x Pi = 4 x Pi.
Why aren’t geometricians good at tennis?
Because they continually try to fold the net into a cube.
Because they continually try to fold the net into a cube.
I asked three people what pi is:
Geometrician: The ratio of a circle’s circumference to its diameter.
Mathematician: 3.14159265…
Engineer: About 3
Geometrician: The ratio of a circle’s circumference to its diameter.
Mathematician: 3.14159265…
Engineer: About 3
There are a large number of proofs of this proposition online; the one below is among the simplest
_
