because 150k injects to cartridge sqrt(150/47)=sqrt(3.19)=1.79=5dB less Johnson`s noise current vs 47k / In=((4*K*T*BW) /R)^0.5 . Please also keep in mind that system input is not amp imput but break in the cartridge ground lead.
Last edited:
In a nutshell, the penny dropped - and this was the key sentence.
Nick S.,
You're right and I was wrong. I think this paradox will bring joy to generations to come - and in many cases the knot will tie itself again and again.
thx
Use please PhonoLCR [ https://www.patreon.com/posts/45-kgts-vmesto-70415214 - 50 kbytes without installation ] if MC12 seems too complex
Attachments
... these gimmicks are nice, but I personally don't need a software tool for this, I just do the math in my head.
But,
thx to Wayne Stegall 👍
me too, but I don't remember where my paper and pencil are anymore
If you need the spreadsheet, here it is in *.ods format. The original is from @SY, I just edited it a bit ..!
fc = sqrt(fh*fl)
and
not
fc=(fh+fl)/2
it is actually the geometric mean and not the arithmetic mean, whether this is of elementary importance for the entire approximation (because it is not anything other than an approximation) remains to be questioned.
HBt.
Psst
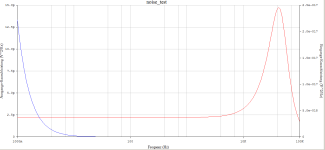
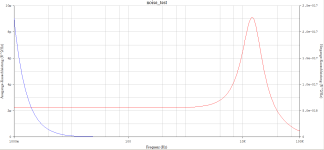
The Uth^2 in the bands is added up, formed from 4*T*k*BW_n * Re(Zp(jOmega_n)). That is a very interesting point, because the real part of the complex equivalent parallel resonant circuit is used as a very simple equivalent of the much more difficult to understand relationship with the correct thermal noise current - in conjunction with the magnetic pickup.
fc = sqrt(fh*fl)
and
not
fc=(fh+fl)/2
it is actually the geometric mean and not the arithmetic mean, whether this is of elementary importance for the entire approximation (because it is not anything other than an approximation) remains to be questioned.
HBt.
Psst
The Uth^2 in the bands is added up, formed from 4*T*k*BW_n * Re(Zp(jOmega_n)). That is a very interesting point, because the real part of the complex equivalent parallel resonant circuit is used as a very simple equivalent of the much more difficult to understand relationship with the correct thermal noise current - in conjunction with the magnetic pickup.
Attachments
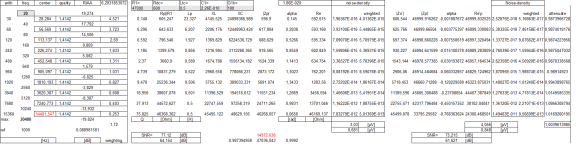
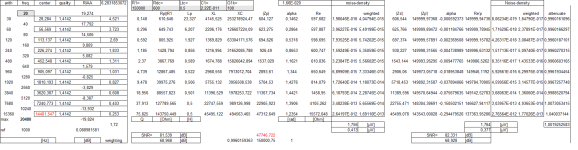
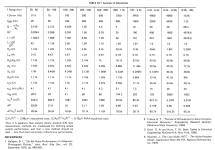
The comparison of methods provides interesting insights. In the left part of the table, the quasi-equivalent band noise of the real part of an equivalent (RCL-parallel-equivalent) circuit is approximated and in the right part the more complex Sukhov-Gefel-Method is applied.
Attachments
Long story short:
It is now fair to assume that an SNR value of 79dB (81dB) will never be achieved. It gets worse with the inherent noise of the connected RIAA preamplifier and especially its i_n.
If we are looking for the best possible SN distance, we have to fall back on Nick's method. The preamp belongs in the chassis, directly at the end of the tonearm cabling.
But, and this is (very) confusing, nowhere in the technical literature (that I know of) is Nick's or Marcel's calculation approach presented - but the termination with 150k compared to 47k should theoretically show a gain of somewhere between +5dB and +10dB. The two example calculations show a gain of between 4.814dB and 7.307dB. Whether my RIAA low pass center of gravity weighting is correct (for equivalent bands), I do not know. Since we can solve everything numerically much more elegantly than with a 10 keypoints spreadsheet - I like an approximation in the form "over the thumb" better: 69dB + 12dB(RIAA gain) = 81dB limit.
HBt.
Psst
Now select the best operational amplifier for the task.
It is now fair to assume that an SNR value of 79dB (81dB) will never be achieved. It gets worse with the inherent noise of the connected RIAA preamplifier and especially its i_n.
If we are looking for the best possible SN distance, we have to fall back on Nick's method. The preamp belongs in the chassis, directly at the end of the tonearm cabling.
But, and this is (very) confusing, nowhere in the technical literature (that I know of) is Nick's or Marcel's calculation approach presented - but the termination with 150k compared to 47k should theoretically show a gain of somewhere between +5dB and +10dB. The two example calculations show a gain of between 4.814dB and 7.307dB. Whether my RIAA low pass center of gravity weighting is correct (for equivalent bands), I do not know. Since we can solve everything numerically much more elegantly than with a 10 keypoints spreadsheet - I like an approximation in the form "over the thumb" better: 69dB + 12dB(RIAA gain) = 81dB limit.
HBt.
Psst
Now select the best operational amplifier for the task.
*.ods
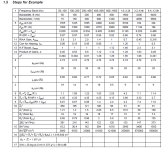
Both methods are now combined, another form. If you have any questions, please ask them.
thermal noise,
as equivalent voltage in selected frequency bands:
You're welcome my friends,
HBt.
as equivalent voltage in selected frequency bands:
You're welcome my friends,
HBt.
Anyone have the 2 makers datasheets which show the precise calculation of RIAA preamp noise spectrum? They were precise & easy to understand. I think we found both papers in Wayne Kirkwood's thread on his website. My single remaining brain cell dun unnerstan htbaudio's calculations.
The important bit in each frequency band IIRC, is transforming the Complex Impedance of the cartridge (which includes the 47k & any capacitance) into an equivalent noise series resistance and a series inductance.
I might be wrong as I last did such hard sums in da previous Millenium
The important bit in each frequency band IIRC, is transforming the Complex Impedance of the cartridge (which includes the 47k & any capacitance) into an equivalent noise series resistance and a series inductance.
I might be wrong as I last did such hard sums in da previous Millenium
The National Semiconductor note is AN 104 https://www.ti.com/lit/an/snva515c/snva515c.pdf see sections 1.4 & 1.5 IIRC, the AD note was an early OP27 datasheet.
It came about from a discussion on Wayne Kirkwood's site https://www.proaudiodesignforum.com/forum/php/viewtopic.php?t=423&hilit=ricardo+riaa&start=10
There's links to NJM 2068 tests and loadsa Real Life noise measurements with various MM cartridges & OPAs.
Many memories from the time when my single remaining brain cell had enough shelf life to pose as a pseudo guru even with the likes of Gurus Wurcer, Wayne & John Roberts present 😊
I'm surprised that 10 yrs on, 5532/4 is STILL one of the best for RIAA MM ... only beaten slightly by a few HUGELY $$$ FET OPAs like OPA 627 and Unobtainium stuff like NJM 2068
In theory, any FET i/p OPA with env < 3nV/rt(Hz) & low 1/f, popcorn bla bla noise should trash 5534AN with a real MM cartridge.
I now have enough info to redo my own version of AN 104 to get a "single noise number" using CCIR 468 2kHz instead of EVIL A wt ... but don't hold your breath waiting cos there's loadsa beach bum issues in the way.
It came about from a discussion on Wayne Kirkwood's site https://www.proaudiodesignforum.com/forum/php/viewtopic.php?t=423&hilit=ricardo+riaa&start=10
There's links to NJM 2068 tests and loadsa Real Life noise measurements with various MM cartridges & OPAs.
Many memories from the time when my single remaining brain cell had enough shelf life to pose as a pseudo guru even with the likes of Gurus Wurcer, Wayne & John Roberts present 😊
I'm surprised that 10 yrs on, 5532/4 is STILL one of the best for RIAA MM ... only beaten slightly by a few HUGELY $$$ FET OPAs like OPA 627 and Unobtainium stuff like NJM 2068
In theory, any FET i/p OPA with env < 3nV/rt(Hz) & low 1/f, popcorn bla bla noise should trash 5534AN with a real MM cartridge.
I now have enough info to redo my own version of AN 104 to get a "single noise number" using CCIR 468 2kHz instead of EVIL A wt ... but don't hold your breath waiting cos there's loadsa beach bum issues in the way.
My calculations are also precise.
Are you talking about the last loud thoughts on the way to a program code? But they are really trivial. But I still have three brain cells left.
It can only ever be the real part of a complex impedance/ resistance (not reactance). Either you carry out the transformation mentioned by Marcel and Nick, or you work with an equivalent, parallel two-pole.
So in the 1980s and 1990s when we were allowed to read your papers. That was a long time ago, but the MM cartridge system is even older - and the hi-fi systems of the early 1970s weren't bad at all, were they? During this time, the CD audio system was also developed and slowly brought to market maturity, while these large laser disks with videos on them already existed.
So a dramatic calculation can no longer be that difficult today, and it's not about simply copying, but about understanding, so that our three (or one!) remaining brain cells can bring the sleepers back to life.
😎☕🏊♂️
HBt.
thx Richard,
memories can keep us alive. Too many friends and companions die far too soon, but some have each left us a personal gift, a fond memory and inspiration.
These (generally valid) points always amaze me too, because they clearly show that no real development in a further positive direction has taken place.
Bear in mind that I am not a fan of the rating /weighting filters either.
Dear Richard,
please publish your complete calculations here in this thread - so that our beach will be clean again.
kindly,
HBt.
⛵
As we can see, H(jOmega|_riaa generates an SNR gain of 20*log(2.98/0.75), approx 12dB. In other words, our equivalent noise bandwidth is (pi/2) * (1/(2*Pi*75µs)) = 1/(4*75µs).
3333.333 Hz
3333.333 Hz
