That assumes da weightings accurately indicate how yucky a particular type of noise is. We know for a fact that IEC-A on capacitor mikes is dominated by da 1G + capsule capacitanc noise and this has only a secondary effect on yuckiness. Dip Ing Wuttke of Schoeps and I are both agreed and have investigated this thoroughly, me in this Millenium.For an adequate assessment of noise, it is also necessary to take into account the weighting according to IEC-A or ITU-R. If roughly rounded, then we take into account only that part of the spectrograms that is higher (on the right) 1 kHz @ #9 message
A 'similar' situation holds for MM RIAA. I've got some measurements circa 1980 under a pile of diving & boating junk but didn't investigate this as thoroughly.
ITU-R 468 is better but still flawed for a 'single number measurement'. There's an AES paper by Eric Benjamin's former boss at Dolby explaining some of the subtleties.
If you twisted my arm, I would confess my old 'favourite' would be ITU 468-ARM, the method dreamt up by Ray Dolby (& Robinson IIRC) using an Average Reading Meter (ARM). Today, 21st century digits make RMS easier then ARM; a reverse of da position in da 1980 & 90s
But today, it's also easy to show a full spectrum so there's no excuse for a single number unless for the Marketing Vice President 😊
OPu=
OPi=
G1k=
Rq=
Ltc=
Rdc=
R1=
R2=
R3=
df=
T=
99.0099 7500 3112.292 10000 100 3333 47000
2.234235e-007[V] 2.256577e-005[V] 86.3153[dB]
4.939737e-007[V] 4.989135e-005[V] 79.4238[dB]
short 1.749524e-005[V] 89.121[dB]
open 0.0001110145[V] 73.07181[dB]
infinite 1.914475e-005[V] 88.3384[dB] Riq= 3333[Ohm]
#
This is still another version on the way to the final algorithm, noise_1_1.exe :
Among other things, "df" is now set by default to the equivalent noise bandwidth of the system (RIAA-MM preamplifier). Let's see if everything is self-explanatory, or if questions arise and are boldly asked?
Let's have fun,
HBt.
OPi=
G1k=
Rq=
Ltc=
Rdc=
R1=
R2=
R3=
df=
T=
99.0099 7500 3112.292 10000 100 3333 47000
2.234235e-007[V] 2.256577e-005[V] 86.3153[dB]
4.939737e-007[V] 4.989135e-005[V] 79.4238[dB]
short 1.749524e-005[V] 89.121[dB]
open 0.0001110145[V] 73.07181[dB]
infinite 1.914475e-005[V] 88.3384[dB] Riq= 3333[Ohm]
#
This is still another version on the way to the final algorithm, noise_1_1.exe :
Among other things, "df" is now set by default to the equivalent noise bandwidth of the system (RIAA-MM preamplifier). Let's see if everything is self-explanatory, or if questions arise and are boldly asked?
Let's have fun,
HBt.
Attachments
@MarcelvdG
How would you calculate?
As explained in Electronics World October 2003 and Linear Audio vol. 8, September 2014. See
"Noise and moving-magnet cartridges", Electronics World October 2003, pages 38...43, https://worldradiohistory.com/UK/Wireless-World/00s/Electronics-World-2003-10-S-OCR.pdf Mind you, Electronics World drew one of the sections of the gain switch in the wrong state in figure 5 and I mixed up the terms spectral density and power spectral density.
See also
https://linearaudio.net/grammophone-preamplifier-noise-calculations-3852-hz-rule-revisited
But today, it's also easy to show a full spectrum so there's no excuse for a single number unless for the Marketing Vice President 😊
Or unless you are a designer and want to optimize a design. By tweaking circuit parameters, you can in general realize an uncountable infinity of different noise spectra. You need some sort of goal function to figure out which is best, or at least reasonably close to it.
Then you'd better choose your 'weighting' carefully. eg if you used IEC A, you would come up with very sub-optimal audible / obtrusive noise performance for Capacitor Mikes, Self Dithering Anti-Aliasing & other Digital Filters and probably MM RIAA too. I've been actively involved in design applying spectrums for the first two cases which is why I'm prejudiced against IEC AOr unless you are a designer and want to optimize a design. By tweaking circuit parameters, you can in general realize an uncountable infinity of different noise spectra. You need some sort of goal function to figure out which is best, or at least reasonably close to it.
Marcel, from the curves Mark posted in #9, I don't think a single figure ITU-468 ranking will differ much from what you'd decide by looking at the curves ... which you have to generate anyway to get the ITU-468 number.
I don't think you are a Marketing VP 😊
The discussion is actually only of academic interest for moving-magnet RIAA amplifiers, because the noise optima are broad anyway. You just have to make sure you are not way off. An amplifier designed to be optimal with RIAA- and A-weighting will be nearly optimal with RIAA- and ITU-R 468-weighting and the other way around.
Still, in general, if a system designer would tell me to look at the spectra without telling me exactly how to judge if spectrum A is better or worse than spectrum B, I wouldn't know what to do.
Still, in general, if a system designer would tell me to look at the spectra without telling me exactly how to judge if spectrum A is better or worse than spectrum B, I wouldn't know what to do.
ref #24
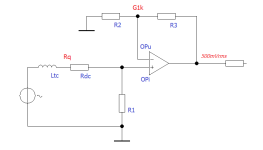
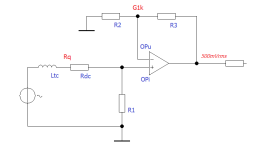
My concern is to capture all noise sources (in the end we always form noise voltages from them), in the example of the feedback system (nfb) the feedback network also contributes a certain amount. We have an operational amplifier (e_n & i_n) and four working /acting /effective resistors. Rq&R1 and also R2&R3: the fact that R3 converts the complex RIAA part is just as clear as the fact that Rq increases with frequency from a certain frequency - Rq is not the coil DC resistance.
One can assume PI/2 times fh_riaa as the equivalent noise bandwidth in the first access. But we only check (with the tool, the simple algorithm) to compare which of the common operational amplifiers (IC) is fundamentally better suited as a non-inverting amplifier (as MM-Pre).
My concern is to capture all noise sources (in the end we always form noise voltages from them), in the example of the feedback system (nfb) the feedback network also contributes a certain amount. We have an operational amplifier (e_n & i_n) and four working /acting /effective resistors. Rq&R1 and also R2&R3: the fact that R3 converts the complex RIAA part is just as clear as the fact that Rq increases with frequency from a certain frequency - Rq is not the coil DC resistance.
One can assume PI/2 times fh_riaa as the equivalent noise bandwidth in the first access. But we only check (with the tool, the simple algorithm) to compare which of the common operational amplifiers (IC) is fundamentally better suited as a non-inverting amplifier (as MM-Pre).
ref #25, 26, 27
Exactly, and that's why it's good to have a specific parameter in hand, as a single value, for example an SNR related to the nominal, resulting useful output voltage to the total noise voltage to be assumed at the output.
We can safely forget all the different evaluation filters (for weigthing or rating) because we do not carrying out a noise measurement "LÄRM" that is relevant to the work-place "ARBEIT". Noise is, after all, a statistical quantity, and we can therefore only consider it as a density function, the certain comparable noise power. Of course, we also like to speak of a color (in comparison with light), the colored noise. Of course, we immediately derive a spectrum from this.
What we do not want is an RMS power spectrum that increases with increasing frequency as y in the x direction.
I don't like Phyton! If you have internalized C (and of course C++), as well as Pascal and Basic, you can read Phyton directly. I can read.
It doesn't matter whether you also plot H(jOmega)_riaa_noisedichte ... we need integrals ..!
HBt.
Psst
A noise voltage behavior that increases with frequency is what we want to avoid at all costs. We don't want an unpleasant, sharp-sounding noise with a lot of energy in the upper octaves.
Exactly, and that's why it's good to have a specific parameter in hand, as a single value, for example an SNR related to the nominal, resulting useful output voltage to the total noise voltage to be assumed at the output.
We can safely forget all the different evaluation filters (for weigthing or rating) because we do not carrying out a noise measurement "LÄRM" that is relevant to the work-place "ARBEIT". Noise is, after all, a statistical quantity, and we can therefore only consider it as a density function, the certain comparable noise power. Of course, we also like to speak of a color (in comparison with light), the colored noise. Of course, we immediately derive a spectrum from this.
What we do not want is an RMS power spectrum that increases with increasing frequency as y in the x direction.
def input_noise_density (Ls, Rs, Ve, Ie, f):
w = 2 * pi * f
Zs = Parallel (Rs + w * 1j * Ls, Rl)
Vn_I = abs (Zs * Ie)
Vn_V = Ve
Vn_Rs = Rnoise (Rs)
Vn_total = sqrt (sqr(Vn_Rs) + sqr(Vn_V) + sqr (Vn_I))
Mark T's code is incorrect, to put it kindly, incomplete. At the same time, it equates the value of the frequency-dependent impedance (of the simple MM model) with the effective resistive component and forms an equivalent resistor with the termination. Thermal noise is referred here solely and alternatively to the DC coil resistance.return Vn_total
I don't like Phyton! If you have internalized C (and of course C++), as well as Pascal and Basic, you can read Phyton directly. I can read.
It doesn't matter whether you also plot H(jOmega)_riaa_noisedichte ... we need integrals ..!
HBt.
Psst
A noise voltage behavior that increases with frequency is what we want to avoid at all costs. We don't want an unpleasant, sharp-sounding noise with a lot of energy in the upper octaves.
Last edited:
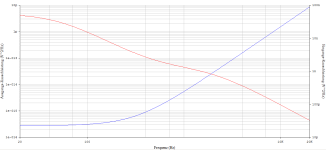
We all opt for the OP of the black curve.(...) from the curves Mark posted in #9, I don't think a single figure ITU-468 ranking will differ much from what you'd decide by looking at the curves ... which you have to generate anyway to get the ITU-468 number.
OPA627
plot_curve (create_reponse_function (Ls, Rs, 4.0e-9, 48e-15), 'k', 'OPA627')
# setup cartridge parameters
Ls = 0.5
Rs = 1000.0
# load resistor
Rl = 47e3 # load resistance (constant)
ITU-R 468 "Bewertungsfilter"
Everyone can reflect on the meaning for themselves. It is not worth arguing, because definitions are agreements and not dictates. Even if autocracy is currently enjoying a global boom.
Let's just stick with the schematic from my opening post #1.
HBt.
Everyone can reflect on the meaning for themselves. It is not worth arguing, because definitions are agreements and not dictates. Even if autocracy is currently enjoying a global boom.
Let's just stick with the schematic from my opening post #1.
HBt.
Another comparison can also be made, namely between a hypothetical SNR determination with an open input and with a shorted input, at full bandwidth and the maximum gain by weighting with the RIAA low-pass filter, related to a tone with a frequency of 1kHz.
Then you can already see between which limits (here a TL081, as noiseless device) a maximum characteristic value (here the SNR, Uout nominally 500mVrms) with a connected MM system can theoretically move. These limits shift almost equally and simultaneously upwards or downwards, in the first simple approximation, depending on the op-amp used.
In other words, the subjectively perceived loudness of the (white) noise is only half as disturbing and is masked during operation, i.e. when playing a record. Thank goodness we color the noise and now it is far more than a quarter as loud, even less disturbing due to the loudness ratings of our hearing apparatus.
And so on and so forth ...
Then you can already see between which limits (here a TL081, as noiseless device) a maximum characteristic value (here the SNR, Uout nominally 500mVrms) with a connected MM system can theoretically move. These limits shift almost equally and simultaneously upwards or downwards, in the first simple approximation, depending on the op-amp used.
In other words, the subjectively perceived loudness of the (white) noise is only half as disturbing and is masked during operation, i.e. when playing a record. Thank goodness we color the noise and now it is far more than a quarter as loud, even less disturbing due to the loudness ratings of our hearing apparatus.
And so on and so forth ...
Attachments
new version
I think, slowly but surely, no reader can really follow the red thread anymore, because he does not know it yet and has forgotten that we (EEs) do not have to use absolute level measures, but that we very often use relations, i.e. ratios ... and declare them to be the measure of all things. In plain language, this means that it is relative and not absolute. But the comparison is absolute within the staking out (the agreement and the reference there).
The last value within the third output line is decisive, because only it takes into account all weighting factors and shifts all sources correctly. The usual, i.e. all other simplifications (of technical articles, textbooks) are inadequate ... as is usually confirmed by measurements in reality.
My personal thanks go directly to Pavel M., whose recent interventions on the subject ( @PMA ) have provided metrological proof - completely unintentionally. Often we are not aware of what we are triggering.
The correct weight factors result in (I won't reveal any more) :
A0=1
A1=( Rq/R1)^2
A2=((R1+Rq)/R1)^2
A3=(R2/(R2+R3))^2
A4=(R3/(R2+R3))^2
A5=((R2*R3)/(R2+R3) * ((R1+Rq)/R1) + Rq)^2
kindly,
HBt.
OPu=
OPi=
G1k=
Rq=
Ltc=
Rdc=
R1=
R2=
R3=
df=
T=
99.0099 7500 3112.292 10000 100 3333 47000
2.234235e-007[V] 2.256577e-005[V] 86.3153[dB]
4.939737e-007[V] 4.989135e-005[V] 79.4238[dB]
short 1.749524e-005[V] 89.121[dB]
open 0.0001110145[V] 73.07181[dB]
infinite 1.914475e-005[V] 88.3384[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 1.749421e-005[V] 88.52641[dB]
reference 0.4668905[V] 1.749373e-005[V] 88.52665[dB]
OPu=
C:\Windows\System32>
I think, slowly but surely, no reader can really follow the red thread anymore, because he does not know it yet and has forgotten that we (EEs) do not have to use absolute level measures, but that we very often use relations, i.e. ratios ... and declare them to be the measure of all things. In plain language, this means that it is relative and not absolute. But the comparison is absolute within the staking out (the agreement and the reference there).
The last value within the third output line is decisive, because only it takes into account all weighting factors and shifts all sources correctly. The usual, i.e. all other simplifications (of technical articles, textbooks) are inadequate ... as is usually confirmed by measurements in reality.
My personal thanks go directly to Pavel M., whose recent interventions on the subject ( @PMA ) have provided metrological proof - completely unintentionally. Often we are not aware of what we are triggering.
The correct weight factors result in (I won't reveal any more) :
A0=1
A1=( Rq/R1)^2
A2=((R1+Rq)/R1)^2
A3=(R2/(R2+R3))^2
A4=(R3/(R2+R3))^2
A5=((R2*R3)/(R2+R3) * ((R1+Rq)/R1) + Rq)^2
kindly,
HBt.
Attachments
If we look at the entire circuit diagram and also take into account the influence of the nfb, a completely different picture of the ranking list emerges:
1)
OP27
OPu=3e-9
OPi=0.4e-12
99.0099 7500 3112.292 10000 100 3333 47000
2.234235e-007[V] 2.256577e-005[V] 86.3153[dB]
4.939737e-007[V] 4.989135e-005[V] 79.4238[dB]
short 1.749524e-005[V] 89.121[dB]
open 0.0001110145[V] 73.07181[dB]
infinite 1.914475e-005[V] 88.3384[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 1.749421e-005[V] 88.52641[dB]
reference 0.4668905[V] 1.749373e-005[V] 88.52665[dB]
2)
LT1028
OPu=0.85e-9
OPi=1e-12
99.0099 850 3112.292 10000 100 3333 47000
3.628418e-007[V] 3.664702e-005[V] 82.10353[dB]
4.954612e-007[V] 5.004158e-005[V] 79.39768[dB]
short 4.990064e-006[V] 100.0173[dB]
open 0.0002741136[V] 65.22079[dB]
infinite 2.006589e-005[V] 87.93023[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 4.967555e-006[V] 99.46145[dB]
reference 0.4668905[V] 4.956958e-006[V] 99.48[dB]
3)
NE5524
OPu=5e-9
OPi=0.7e-12
99.0099 7142.857 3112.292 10000 100 3333 47000
2.27244e-007[V] 2.295165e-005[V] 86.16802[dB]
5.640794e-007[V] 5.697201e-005[V] 78.27107[dB]
short 2.915899e-005[V] 84.68395[dB]
open 0.000194051[V] 68.22108[dB]
infinite 3.217668e-005[V] 83.82858[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 2.915711e-005[V] 84.08942[dB]
reference 0.4668905[V] 2.915622e-005[V] 84.08968[dB]
4)
OPA627
OPu=8e-9
OPi=1.6e-15
99.0099 5000000 3112.292 10000 100 3333 47000
1.033774e-008[V] 1.044111e-006[V] 113.0094[dB]
6.692981e-007[V] 6.75991e-005[V] 76.78548[dB]
short 4.66499e-005[V] 80.60239[dB]
open 4.665196e-005[V] 80.60201[dB]
infinite 4.664991e-005[V] 80.60239[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 4.66499e-005[V] 80.00729[dB]
reference 0.4668905[V] 4.66499e-005[V] 80.00729[dB]
5)
AD825
OPu=12e-9
OPi=10e-15
99.0099 1200000 3112.292 10000 100 3333 47000
2.108041e-008[V] 2.129121e-006[V] 106.8203[dB]
8.682124e-007[V] 8.768946e-005[V] 74.52535[dB]
short 6.997485e-005[V] 77.08056[dB]
open 7.00285e-005[V] 77.07391[dB]
infinite 6.997513e-005[V] 77.08053[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 6.997485e-005[V] 76.48546[dB]
reference 0.4668905[V] 6.997485e-005[V] 76.48546[dB]
6)
TL071
OPu=18e-9
OPi=10e-15
99.0099 1800000 3112.292 10000 100 3333 47000
1.721974e-008[V] 1.739194e-006[V] 108.5773[dB]
1.200795e-006[V] 0.0001212803[V] 71.7085[dB]
short 0.0001049623[V] 73.55874[dB]
open 0.000104998[V] 73.55578[dB]
infinite 0.0001049625[V] 73.55872[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 0.0001049623[V] 72.96364[dB]
reference 0.4668905[V] 0.0001049623[V] 72.96364[dB]
7)
LM741
OPu=20e-9
OPi=0.3e-12
99.0099 66666.67 3112.292 10000 100 3333 47000
8.747415e-008[V] 8.834889e-006[V] 94.46028[dB]
1.31757e-006[V] 0.0001330745[V] 70.9024[dB]
short 0.0001166249[V] 72.64358[dB]
open 0.000142694[V] 70.89129[dB]
infinite 0.0001167705[V] 72.63274[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 0.0001166248[V] 72.04848[dB]
reference 0.4668905[V] 0.0001166248[V] 72.04848[dB]
However, this does not mean that the subjectively perceived noise and interference spectrum in relation to the complex, lossy internal resistance of the tactile pickup must necessarily follow (in) this order.
Actually, the two OPs LT1028 and OP27 now share the gold medal, with the LT1028 clearly shining more brightly. Some listeners just don't like this shine! And when playing a normal, average long-playing record, there are hardly any differences in the resulting SNR parameter!
Bye,
HBt.
(compare it to ref #2)
1)
OP27
OPu=3e-9
OPi=0.4e-12
99.0099 7500 3112.292 10000 100 3333 47000
2.234235e-007[V] 2.256577e-005[V] 86.3153[dB]
4.939737e-007[V] 4.989135e-005[V] 79.4238[dB]
short 1.749524e-005[V] 89.121[dB]
open 0.0001110145[V] 73.07181[dB]
infinite 1.914475e-005[V] 88.3384[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 1.749421e-005[V] 88.52641[dB]
reference 0.4668905[V] 1.749373e-005[V] 88.52665[dB]
2)
LT1028
OPu=0.85e-9
OPi=1e-12
99.0099 850 3112.292 10000 100 3333 47000
3.628418e-007[V] 3.664702e-005[V] 82.10353[dB]
4.954612e-007[V] 5.004158e-005[V] 79.39768[dB]
short 4.990064e-006[V] 100.0173[dB]
open 0.0002741136[V] 65.22079[dB]
infinite 2.006589e-005[V] 87.93023[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 4.967555e-006[V] 99.46145[dB]
reference 0.4668905[V] 4.956958e-006[V] 99.48[dB]
3)
NE5524
OPu=5e-9
OPi=0.7e-12
99.0099 7142.857 3112.292 10000 100 3333 47000
2.27244e-007[V] 2.295165e-005[V] 86.16802[dB]
5.640794e-007[V] 5.697201e-005[V] 78.27107[dB]
short 2.915899e-005[V] 84.68395[dB]
open 0.000194051[V] 68.22108[dB]
infinite 3.217668e-005[V] 83.82858[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 2.915711e-005[V] 84.08942[dB]
reference 0.4668905[V] 2.915622e-005[V] 84.08968[dB]
4)
OPA627
OPu=8e-9
OPi=1.6e-15
99.0099 5000000 3112.292 10000 100 3333 47000
1.033774e-008[V] 1.044111e-006[V] 113.0094[dB]
6.692981e-007[V] 6.75991e-005[V] 76.78548[dB]
short 4.66499e-005[V] 80.60239[dB]
open 4.665196e-005[V] 80.60201[dB]
infinite 4.664991e-005[V] 80.60239[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 4.66499e-005[V] 80.00729[dB]
reference 0.4668905[V] 4.66499e-005[V] 80.00729[dB]
5)
AD825
OPu=12e-9
OPi=10e-15
99.0099 1200000 3112.292 10000 100 3333 47000
2.108041e-008[V] 2.129121e-006[V] 106.8203[dB]
8.682124e-007[V] 8.768946e-005[V] 74.52535[dB]
short 6.997485e-005[V] 77.08056[dB]
open 7.00285e-005[V] 77.07391[dB]
infinite 6.997513e-005[V] 77.08053[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 6.997485e-005[V] 76.48546[dB]
reference 0.4668905[V] 6.997485e-005[V] 76.48546[dB]
6)
TL071
OPu=18e-9
OPi=10e-15
99.0099 1800000 3112.292 10000 100 3333 47000
1.721974e-008[V] 1.739194e-006[V] 108.5773[dB]
1.200795e-006[V] 0.0001212803[V] 71.7085[dB]
short 0.0001049623[V] 73.55874[dB]
open 0.000104998[V] 73.55578[dB]
infinite 0.0001049625[V] 73.55872[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 0.0001049623[V] 72.96364[dB]
reference 0.4668905[V] 0.0001049623[V] 72.96364[dB]
7)
LM741
OPu=20e-9
OPi=0.3e-12
99.0099 66666.67 3112.292 10000 100 3333 47000
8.747415e-008[V] 8.834889e-006[V] 94.46028[dB]
1.31757e-006[V] 0.0001330745[V] 70.9024[dB]
short 0.0001166249[V] 72.64358[dB]
open 0.000142694[V] 70.89129[dB]
infinite 0.0001167705[V] 72.63274[dB] Riq= 3333[Ohm]
reference 0.4668905[V] 0.0001166248[V] 72.04848[dB]
reference 0.4668905[V] 0.0001166248[V] 72.04848[dB]
However, this does not mean that the subjectively perceived noise and interference spectrum in relation to the complex, lossy internal resistance of the tactile pickup must necessarily follow (in) this order.
Actually, the two OPs LT1028 and OP27 now share the gold medal, with the LT1028 clearly shining more brightly. Some listeners just don't like this shine! And when playing a normal, average long-playing record, there are hardly any differences in the resulting SNR parameter!
Bye,
HBt.
(compare it to ref #2)
Here's the CCIR/ARM paper from 1978 -- it was a preprint from an AES convention.ITU-R 468 is better but still flawed for a 'single number measurement'. There's an AES paper by Eric Benjamin's former boss at Dolby explaining some of the subtleties.
If you twisted my arm, I would confess my old 'favourite' would be ITU 468-ARM, the method dreamt up by Ray Dolby (& Robinson IIRC) using an Average Reading Meter (ARM). Today, 21st century digits make RMS easier then ARM; a reverse of da position in da 1980 & 90s
Attachments
I can't say my single remaining brain cell follows da hard sums you do to show this but I can speak from REAL LIFE experience.Actually, the two OPs LT1028 and OP27 now share the gold medal, with the LT1028 clearly shining more brightly. Some listeners just don't like this shine! And when playing a normal, average long-playing record, there are hardly any differences in the resulting SNR parameter!
LT1028 & OP27 are CRAP for MM RIAA. Substituting 5534 or even 5532 will result in obvious noise improvement when you lift the cartridge off the record and (for some people) even when playing a normal, average LP.
(Internal) sourceresistance is now 12000 Ohm!
{
};
Some (entirely expected) shifts are now taking place on the pitches:
1)
OP27
OPu=3e-9
OPi=0.4e-12
G1k=
Rq=12e3
99.0099 7500 9559.322 10000 100 12000 47000
5.421995e-007[V] 5.476215e-005[V] 77.2347[dB]
9.827562e-007[V] 9.925837e-005[V] 72.06898[dB]
short 1.749524e-005[V] 89.121[dB]
open 0.0001110145[V] 73.07181[dB]
infinite 3.300788e-005[V] 83.60705[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 1.749521e-005[V] 87.14594[dB]
reference 0.3983051[V] 1.749373e-005[V] 87.14667[dB]
2)
OPA627
OPu=8e-9
OPi=1.6e-15
G1k=
Rq=12e3
99.0099 5000000 9559.322 10000 100 12000 47000
3.173164e-008[V] 3.204896e-006[V] 101.888[dB]
1.08458e-006[V] 0.0001095426[V] 71.21266[dB]
short 4.66499e-005[V] 80.60239[dB]
open 4.665196e-005[V] 80.60201[dB]
infinite 4.665004e-005[V] 80.60236[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 4.66499e-005[V] 78.6273[dB]
reference 0.3983051[V] 4.66499e-005[V] 78.6273[dB]
3)
NE5534
OPu=5e-9
OPi=0.7e-12
G1k=
Rq=12e3
99.0099 7142.857 9559.322 10000 100 12000 47000
5.47932e-007[V] 5.534113e-005[V] 77.14336[dB]
1.100705e-006[V] 0.0001111712[V] 71.08447[dB]
short 2.915899e-005[V] 84.68395[dB]
open 0.000194051[V] 68.22108[dB]
infinite 5.700458e-005[V] 78.86121[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 2.915895e-005[V] 82.70888[dB]
reference 0.3983051[V] 2.915622e-005[V] 82.70969[dB]
4)
LT1028
OPu=0.85e-9
OPi=1e-12
G1k=
Rq=12e3
99.0099 850 9559.322 10000 100 12000 47000
6.928349e-007[V] 6.997632e-005[V] 75.10529[dB]
1.154957e-006[V] 0.0001166507[V] 70.66657[dB]
short 4.990064e-006[V] 100.0173[dB]
open 0.0002741136[V] 65.22079[dB]
infinite 7.015255e-005[V] 77.05853[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 4.989572e-006[V] 98.04305[dB]
reference 0.3983051[V] 4.956923e-006[V] 98.10007[dB]
5)
AD825
OPu=12e-9
OPi=10e-15
G1k=
Rq=12e3
99.0099 1200000 9559.322 10000 100 12000 47000
6.457513e-008[V] 6.522088e-006[V] 95.71658[dB]
1.263559e-006[V] 0.0001276195[V] 69.88598[dB]
short 6.997485e-005[V] 77.08056[dB]
open 7.00285e-005[V] 77.07391[dB]
infinite 6.997835e-005[V] 77.08012[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 6.997485e-005[V] 75.10548[dB]
reference 0.3983051[V] 6.997485e-005[V] 75.10548[dB]
6)
TL071
OPu=18e-9
OPi=10e-15
G1k=
Rq=12e3
99.0099 1800000 9559.322 10000 100 12000 47000
5.279568e-008[V] 5.332363e-006[V] 97.46592[dB]
1.594389e-006[V] 0.0001610333[V] 67.866[dB]
short 0.0001049623[V] 73.55874[dB]
open 0.000104998[V] 73.55578[dB]
infinite 0.0001049646[V] 73.55854[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 0.0001049623[V] 71.58366[dB]
reference 0.3983051[V] 0.0001049623[V] 71.58366[dB]
7)
LM741
OPu=20e-9
OPi=0.3e-12
G1k=
Rq=12e3
99.0099 66666.67 9559.322 10000 100 12000 47000
2.57077e-007[V] 2.596477e-005[V] 83.71663[dB]
1.727813e-006[V] 0.0001745091[V] 67.16795[dB]
short 0.0001166249[V] 72.64358[dB]
open 0.000142694[V] 70.89129[dB]
infinite 0.0001184991[V] 72.5051[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 0.0001166249[V] 70.6685[dB]
reference 0.3983051[V] 0.0001166248[V] 70.6685[dB]
Now the question naturally arises at which signal frequency the generalized representative “Rq” is exactly 12kOhm - and of course in reality there is a complex internal resistance, with R_series +jXL_series. We all know that these two real and imaginary components are not constant. As the frequency increases, the resistance increases and the reactance decreases.
If Pavel M. were to pick up his test jig again (OpenAmpOne-Project) now and measure, he would confirm exactly this sequence.
I thought that was obvious Richard.
But you are welcome to post your own algorithm for the hard calculation of a quality factor here, I would be happy about that - oh what: I would go swimming and enjoy the beach.
HBt.
{
Less diving and a little more listening and thinking may be helpful in our old age.I can't say my single remaining brain cell follows da hard sums you do to show this but I can speak from REAL LIFE experience.
I hope this has been objectively confirmed by double blind testing and is not just accumulated life experience.LT1028 & OP27 are CRAP for MM RIAA. Substituting 5534 or even 5532 will result in obvious noise improvement when you lift the cartridge off the record and (for some people) even when playing a normal, average LP.
};
Some (entirely expected) shifts are now taking place on the pitches:
1)
OP27
OPu=3e-9
OPi=0.4e-12
G1k=
Rq=12e3
99.0099 7500 9559.322 10000 100 12000 47000
5.421995e-007[V] 5.476215e-005[V] 77.2347[dB]
9.827562e-007[V] 9.925837e-005[V] 72.06898[dB]
short 1.749524e-005[V] 89.121[dB]
open 0.0001110145[V] 73.07181[dB]
infinite 3.300788e-005[V] 83.60705[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 1.749521e-005[V] 87.14594[dB]
reference 0.3983051[V] 1.749373e-005[V] 87.14667[dB]
2)
OPA627
OPu=8e-9
OPi=1.6e-15
G1k=
Rq=12e3
99.0099 5000000 9559.322 10000 100 12000 47000
3.173164e-008[V] 3.204896e-006[V] 101.888[dB]
1.08458e-006[V] 0.0001095426[V] 71.21266[dB]
short 4.66499e-005[V] 80.60239[dB]
open 4.665196e-005[V] 80.60201[dB]
infinite 4.665004e-005[V] 80.60236[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 4.66499e-005[V] 78.6273[dB]
reference 0.3983051[V] 4.66499e-005[V] 78.6273[dB]
3)
NE5534
OPu=5e-9
OPi=0.7e-12
G1k=
Rq=12e3
99.0099 7142.857 9559.322 10000 100 12000 47000
5.47932e-007[V] 5.534113e-005[V] 77.14336[dB]
1.100705e-006[V] 0.0001111712[V] 71.08447[dB]
short 2.915899e-005[V] 84.68395[dB]
open 0.000194051[V] 68.22108[dB]
infinite 5.700458e-005[V] 78.86121[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 2.915895e-005[V] 82.70888[dB]
reference 0.3983051[V] 2.915622e-005[V] 82.70969[dB]
4)
LT1028
OPu=0.85e-9
OPi=1e-12
G1k=
Rq=12e3
99.0099 850 9559.322 10000 100 12000 47000
6.928349e-007[V] 6.997632e-005[V] 75.10529[dB]
1.154957e-006[V] 0.0001166507[V] 70.66657[dB]
short 4.990064e-006[V] 100.0173[dB]
open 0.0002741136[V] 65.22079[dB]
infinite 7.015255e-005[V] 77.05853[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 4.989572e-006[V] 98.04305[dB]
reference 0.3983051[V] 4.956923e-006[V] 98.10007[dB]
5)
AD825
OPu=12e-9
OPi=10e-15
G1k=
Rq=12e3
99.0099 1200000 9559.322 10000 100 12000 47000
6.457513e-008[V] 6.522088e-006[V] 95.71658[dB]
1.263559e-006[V] 0.0001276195[V] 69.88598[dB]
short 6.997485e-005[V] 77.08056[dB]
open 7.00285e-005[V] 77.07391[dB]
infinite 6.997835e-005[V] 77.08012[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 6.997485e-005[V] 75.10548[dB]
reference 0.3983051[V] 6.997485e-005[V] 75.10548[dB]
6)
TL071
OPu=18e-9
OPi=10e-15
G1k=
Rq=12e3
99.0099 1800000 9559.322 10000 100 12000 47000
5.279568e-008[V] 5.332363e-006[V] 97.46592[dB]
1.594389e-006[V] 0.0001610333[V] 67.866[dB]
short 0.0001049623[V] 73.55874[dB]
open 0.000104998[V] 73.55578[dB]
infinite 0.0001049646[V] 73.55854[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 0.0001049623[V] 71.58366[dB]
reference 0.3983051[V] 0.0001049623[V] 71.58366[dB]
7)
LM741
OPu=20e-9
OPi=0.3e-12
G1k=
Rq=12e3
99.0099 66666.67 9559.322 10000 100 12000 47000
2.57077e-007[V] 2.596477e-005[V] 83.71663[dB]
1.727813e-006[V] 0.0001745091[V] 67.16795[dB]
short 0.0001166249[V] 72.64358[dB]
open 0.000142694[V] 70.89129[dB]
infinite 0.0001184991[V] 72.5051[dB] Riq= 12000[Ohm]
reference 0.3983051[V] 0.0001166249[V] 70.6685[dB]
reference 0.3983051[V] 0.0001166248[V] 70.6685[dB]
Now the question naturally arises at which signal frequency the generalized representative “Rq” is exactly 12kOhm - and of course in reality there is a complex internal resistance, with R_series +jXL_series. We all know that these two real and imaginary components are not constant. As the frequency increases, the resistance increases and the reactance decreases.
If Pavel M. were to pick up his test jig again (OpenAmpOne-Project) now and measure, he would confirm exactly this sequence.
I thought that was obvious Richard.
But you are welcome to post your own algorithm for the hard calculation of a quality factor here, I would be happy about that - oh what: I would go swimming and enjoy the beach.
HBt.
Attachments
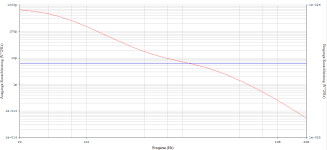
I hope the reader of this thread is now beginning to understand why the LT1028 is now back at the bottom of the rankings and the OPA627 has catapulted itself back to the top, but as PMA's measurement shows, it is not really better than an OP27. Why the 27 should be subjectively worse is not clear from the published spectrum from Prague.
@kgrlee
Would you like to create your own calculation algorithm for us?
Greetings,
HBt.
Psst.
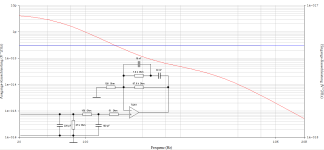
Curves as a function of frequency only appear at the very end of development within a software tool, right?
@kgrlee
Would you like to create your own calculation algorithm for us?
Greetings,
HBt.
Psst.
Curves as a function of frequency only appear at the very end of development within a software tool, right?
Version 1.3
Sorry, but I made a stupid little variable declaration error in the last version, which happens when you're a traveler through the department store of algorithm development.
Now the "rudimentary calculator" (because that's all it is) looks like this:
{
OPu=
OPi=
G1k=
Rq=
Ltc=
Rdc=
R1=
R2=
R3=
df=
T=
99.0099 7500 3112.292 10000 100 3333 47000
2.234235e-007[V] 2.256577e-005[V] 86.3153[dB]
4.939737e-007[V] 4.989135e-005[V] 79.4238[dB]
short 1.749524e-005[V] 89.121[dB]
open 0.0001110145[V] 73.07181[dB]
infinite 1.914475e-005[V] 88.3384[dB] Riq= 3333[Ohm]
reference: 0.4668905[V] 4.598169e-005[V] 80.1326[dB]
reference: 0.4668905[V] 0.0001852986[V] 68.02686[dB]
543.4783[V/A] 3.000000024113862e-009[V/sqrt(Hz)]
9.661835019487091e-006[A/V] 3.999999842123142e-013[A/sqrt(Hz)]
45.59516394204096[dB] 103500[Ohm]
OPu=
C:\Windows\System32>
};
If you don't want to do it yourself, I can only encourage you to play with this strange calculator. The result of the third output line is still decisive. The other issues can safely be regarded as a puzzle, I am very curious to see if anyone can crack this apparent puzzle of issue contents.
kindly,
HBt.
Sorry, but I made a stupid little variable declaration error in the last version, which happens when you're a traveler through the department store of algorithm development.
Now the "rudimentary calculator" (because that's all it is) looks like this:
{
OPu=
OPi=
G1k=
Rq=
Ltc=
Rdc=
R1=
R2=
R3=
df=
T=
99.0099 7500 3112.292 10000 100 3333 47000
2.234235e-007[V] 2.256577e-005[V] 86.3153[dB]
4.939737e-007[V] 4.989135e-005[V] 79.4238[dB]
short 1.749524e-005[V] 89.121[dB]
open 0.0001110145[V] 73.07181[dB]
infinite 1.914475e-005[V] 88.3384[dB] Riq= 3333[Ohm]
reference: 0.4668905[V] 4.598169e-005[V] 80.1326[dB]
reference: 0.4668905[V] 0.0001852986[V] 68.02686[dB]
543.4783[V/A] 3.000000024113862e-009[V/sqrt(Hz)]
9.661835019487091e-006[A/V] 3.999999842123142e-013[A/sqrt(Hz)]
45.59516394204096[dB] 103500[Ohm]
OPu=
C:\Windows\System32>
};
If you don't want to do it yourself, I can only encourage you to play with this strange calculator. The result of the third output line is still decisive. The other issues can safely be regarded as a puzzle, I am very curious to see if anyone can crack this apparent puzzle of issue contents.
kindly,
HBt.
Attachments
- Home
- Source & Line
- Analogue Source
- Quick comparison -> OP-Amp Noise -> Simplified calculation