@auriga2001in 1. It doesn't filter common-mode noise. 2. The output impedance is high and non-linear. It doesn't really address the problems an smps introduces. A 6mH choke in series with the +V rail? I wouldn't use it.
I got a Noyito LC EMI filter for DC (<20A) and placed it between the SMPS and the LISN (measurement conditions equal to those used in the previous measurements):
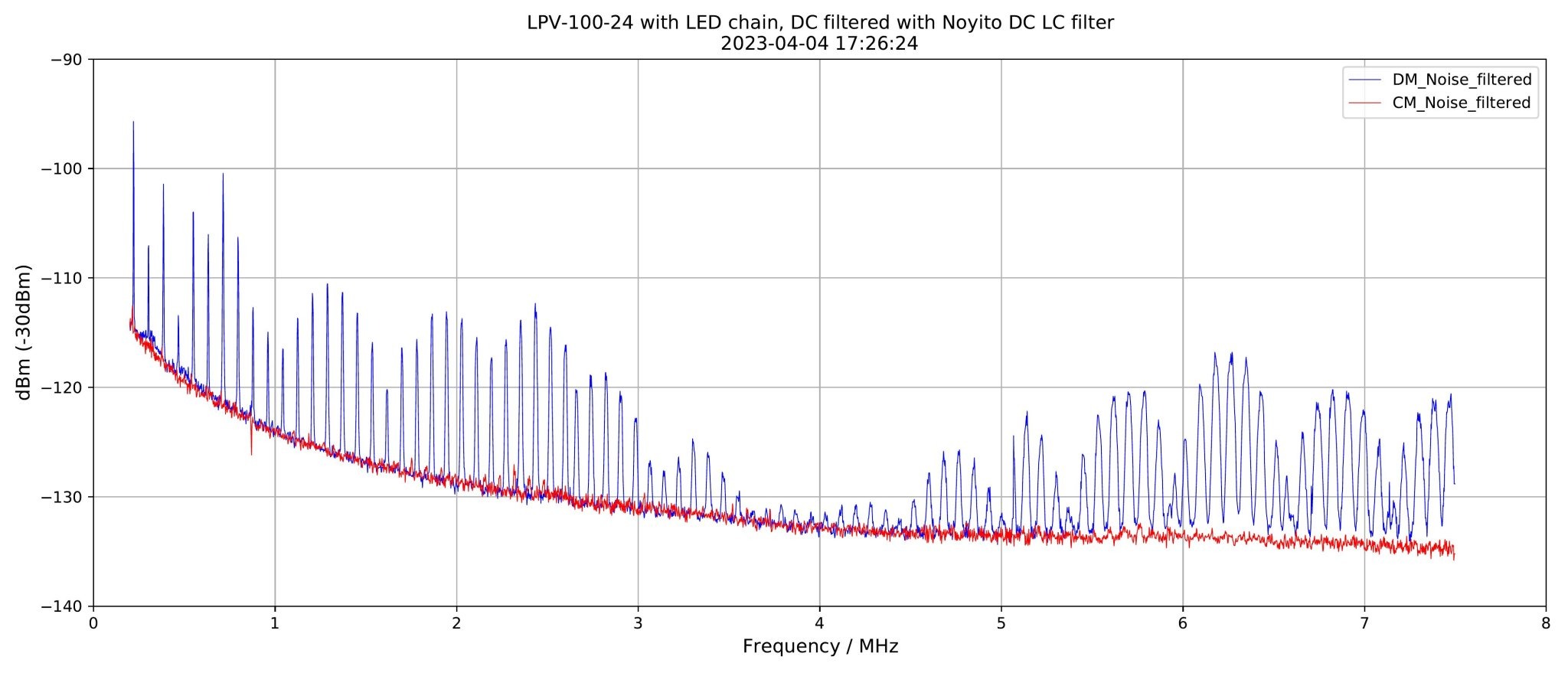
Compared to the unfiltered spectrum, two aspects show up:
a) Common-mode noise is completely below the noise level of the spectrum analyser.
b) The DM noise is substantially lowered with a minimum around 4 MHz, but at higher frequencies attenuation gets smaller almost up to the unfiltered levels. This might be due to the electrolytics in the filter path, which probably become inductive at these high frequencies.
Interpretation: This filter works and noise is reduced to really low levels. Would it be audible? I dont know.
Next step: Measurement with the osci in the frequency range between 0 and 1MHz.
Compared to the unfiltered spectrum, two aspects show up:
a) Common-mode noise is completely below the noise level of the spectrum analyser.
b) The DM noise is substantially lowered with a minimum around 4 MHz, but at higher frequencies attenuation gets smaller almost up to the unfiltered levels. This might be due to the electrolytics in the filter path, which probably become inductive at these high frequencies.
Interpretation: This filter works and noise is reduced to really low levels. Would it be audible? I dont know.
Next step: Measurement with the osci in the frequency range between 0 and 1MHz.
Interesting find. I'll be ordering from Amazon soon and will get one to check out. The 4A one might be more useful for lower output Z.
Any chance you can use log freq axis on your plots? It's so much more useful for audio.
Any chance you can use log freq axis on your plots? It's so much more useful for audio.
And here now the low-frequency range measured with a 16-bit scope and a FFT with 65536 bins and averaging. Red trace without the Noyito filter, blue trace with filter.
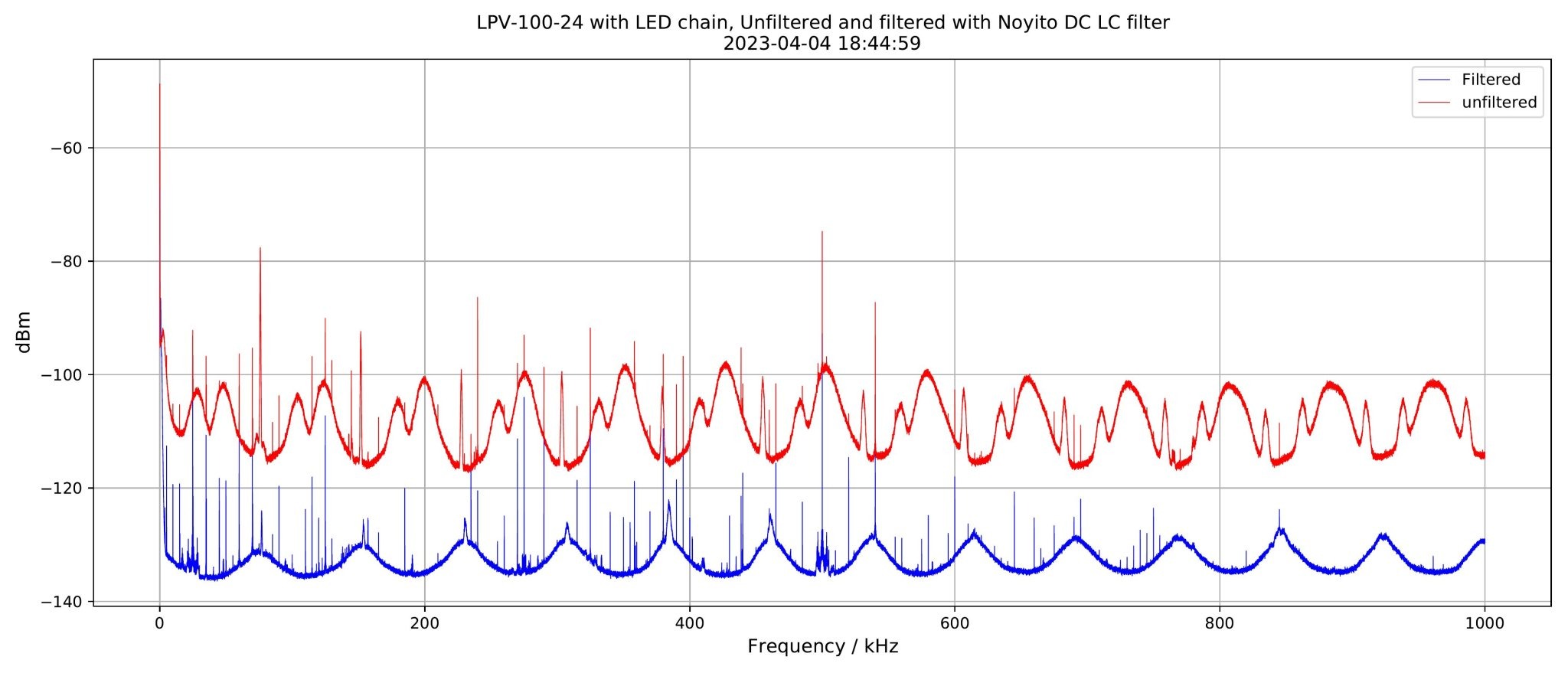
Thanks, but the log plot only goes up to 1kHz.
When overlapping curves using so many bins is actually detrimental, when freq spikes overlap it's hard to tell where the lower one ends.
When overlapping curves using so many bins is actually detrimental, when freq spikes overlap it's hard to tell where the lower one ends.
There is another (complex) option I read in a research paper - active chokes. For example - use a sensing choke, and then have an opamp output attached to a later driving choke. The concept being the sensed noise is then inversely applied to the line by the later driving choke. However, it applies that magically the opamp needs power from somewhere.
I use a couple of cheap 60V adjustable/12/5/3.3v SMPS bench supplies with a ADC currently, the main noise has been removed by 3080s then a set of inductors. However it seems every SMPS seems happy to pass through low frequency noise but I've not noted much of the 120mVpp switching noise out of either of the SMPS. They have the normal common mode and differentials on the mains but also on the output as you'd expect.
I use a couple of cheap 60V adjustable/12/5/3.3v SMPS bench supplies with a ADC currently, the main noise has been removed by 3080s then a set of inductors. However it seems every SMPS seems happy to pass through low frequency noise but I've not noted much of the 120mVpp switching noise out of either of the SMPS. They have the normal common mode and differentials on the mains but also on the output as you'd expect.
Sorry, I missed the "kHz" in the X axis label. This may very well be the best results we've seen so far.
Any reason why activity below 10kHz isn't included?
Any reason why activity below 10kHz isn't included?
Not measured (yet), but I did now:
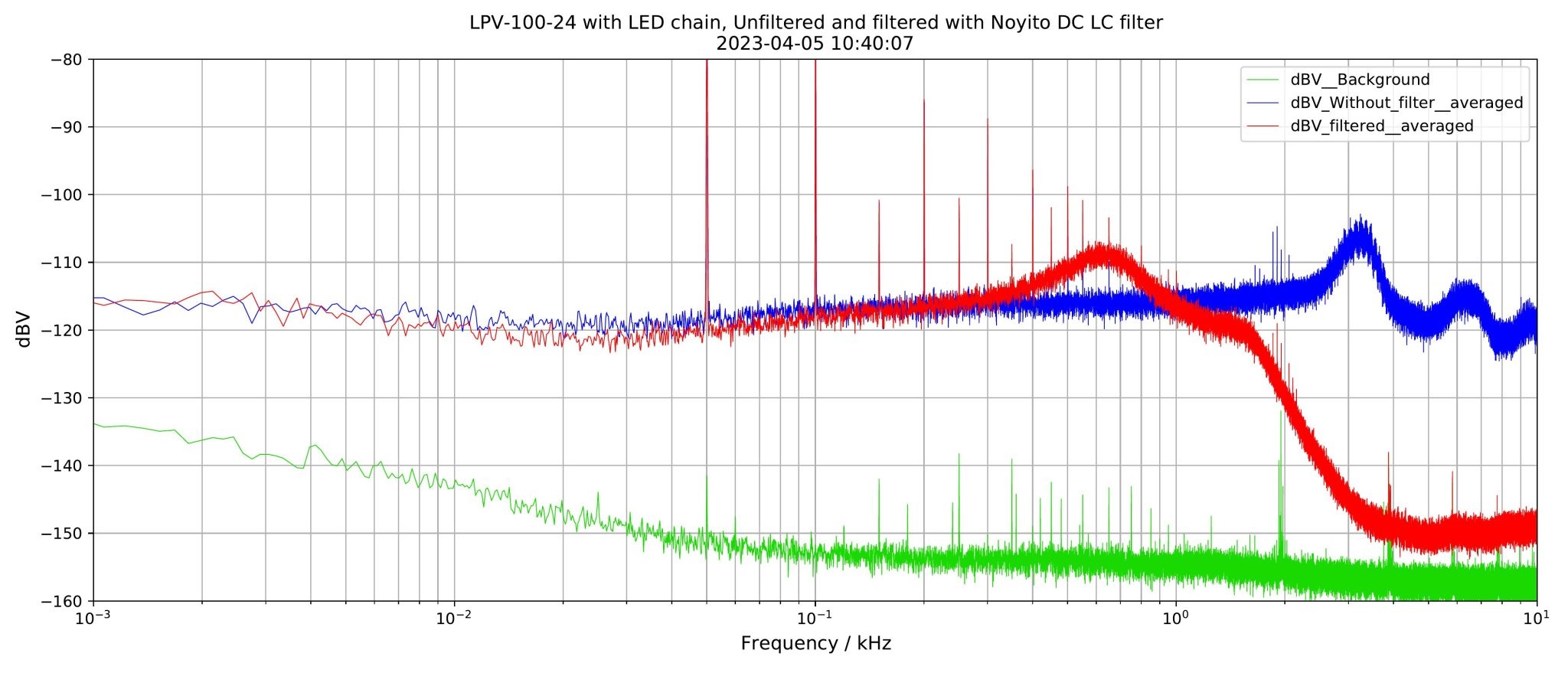
Note that the x axis is again in kHz (comes from the Picoscope program) and starts at 1Hz and goes to 10 kHz.
The background (green trace) shows noise coming from somewhere, the SMPS data contain both noise from the AC mains (50Hz and multiples). The spikes at 50Hz and 100Hz go to -75dBV in both filtered and unfiltered data.
The filter action above about 1kHz is clearly visible, but I would like to mention a caveat with averaged measurements:
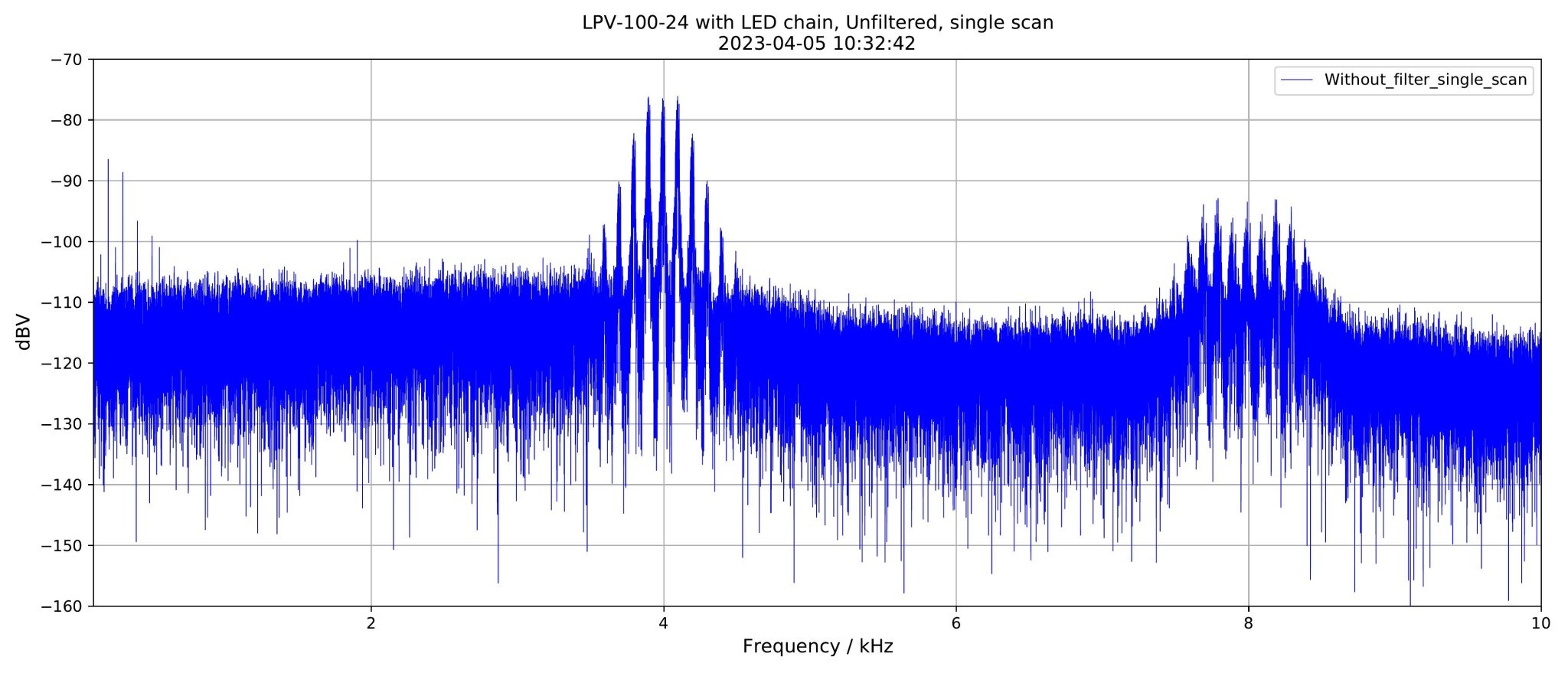
This scan enlarges the bump around 4 kHz and shows peaks reaching substantially above the averaged bump (-78dBV versus -105dBV). I have measured SMPS, which sweep their switching frequency on a second scale. When measuring on a longer time scale with averaging decreases therefore the maxima to a more "pleasant" niveau (and the SMPS may now fulfill the limits according to CISPR in a miraculous way
).
Note that the x axis is again in kHz (comes from the Picoscope program) and starts at 1Hz and goes to 10 kHz.
The background (green trace) shows noise coming from somewhere, the SMPS data contain both noise from the AC mains (50Hz and multiples). The spikes at 50Hz and 100Hz go to -75dBV in both filtered and unfiltered data.
The filter action above about 1kHz is clearly visible, but I would like to mention a caveat with averaged measurements:
This scan enlarges the bump around 4 kHz and shows peaks reaching substantially above the averaged bump (-78dBV versus -105dBV). I have measured SMPS, which sweep their switching frequency on a second scale. When measuring on a longer time scale with averaging decreases therefore the maxima to a more "pleasant" niveau (and the SMPS may now fulfill the limits according to CISPR in a miraculous way
).
Yeah, the frequency is modulating so averaging is combining spectra caught at different times. I still think they would combine more usefully with fewer freq bins in the measurement. This is just TMI.
Boy, that averaging filter has some serious peaking before cutoff!
Boy, that averaging filter has some serious peaking before cutoff!
Damping an LC filter is straightforward but painful. As Bob Cordell says: pick your poison. Either increase the filter's output impedance ("series damping") or increase BOM cost and physical size ("parallel damping") to get rid of peaks in the frequency response // get rid of oscillatory ringing in the transient response. Be sure to include the parasitic R and C of physical inductors in your analysis; also be sure to include the parasitic R and L of physical capacitors in your analysis.
If you've got an impedance meter whose measurement frequency is continuously user-adjustable, you can get pretty good estimates of self-inductance and/or self-capacitance from the Z-versus-f plots, plus a little analysis.
If you've got an impedance meter whose measurement frequency is continuously user-adjustable, you can get pretty good estimates of self-inductance and/or self-capacitance from the Z-versus-f plots, plus a little analysis.
No, this peak does not come from averaging in the scope, it is the noise (smoothed somewhat due to averaging). In a single shot the bumps are already there.
IMHO, the shift of the bumps comes from the changing impedance the SMPS sees at the output, when the filter is inserted between output and load. This changes the pulse width modulation accordingly.
I measured the impedance up to 20MHz with a load of 50Ohm:
Above about 3.5MHz the filter behaves like an inductor, which is (as you mention) probably due to the self-inductance of the elkos (470uF) on the filter board.
The damping of >80dB is in reality spoiled by the ohmic resistance of the LED chain (about 12 Ohm).