By popular demand, here is a new thread devoted to PETTaLS flat panel speaker simulation software, developed by Dr. David Anderson. Flat panel speakers may also be referred to as bending wave speakers, or DML speakers.
Let's use this thread to discuss topics specific to the use of and improvement of this great new tool. Topics could include, but are not limited to:
PETTaLSFree
Some videos about the software are here:
PETTaLS Videos
Eric
Let's use this thread to discuss topics specific to the use of and improvement of this great new tool. Topics could include, but are not limited to:
- new release announcements
- questions about how to use it
- features you'd like to see
- possible bugs
- interpretation of results
- other....
PETTaLSFree
Some videos about the software are here:
PETTaLS Videos
Eric
Last edited:
@Eucyblues99
You wrote:
Left to right: CCCC case - 700x300x3 panel - Q1 used to eliminate 'noise'
(1) Reducing E increases low freq range, no significant effect above 100Hz (for the chosen panel).
(2) Increasing density reduces mid to high level output in a non-linear manner
(3) As for (2) above - pale blue line overlays a SSSS case on the orange CCCC - indicates constraints principally affect low frequencies only.
(4) As for (3) above, red line overlays Q5 SSSS case on the pale blue SSSS Q1
Nice use of Pettals, Eucy. I decided to comment on this here, rather than in the other forum, I hope you don't mind.
One way to understand your observations even better is to look at the equation for the natural frequencies, like the one below. This is the eqn specifically for "simple" supports (SSSS), but it shares a lot of similarities with the equations for other boundary conditions.
The part on the left depends only on the boundary conditions and aspect ratio of the panel, and determines the relative positions along the frequency axis of all the natural frequencies. Hence, that part (along with the exciter position) largely determines the shape of the frequency response curve. That is, it determines where all the peaks and dips will happen relative to each other. Of course, the frequency response of the exciter itself will have some influence, especially at very low and very high frequencies, as will the exciter vc diameter and location of the coincidence frequency (at high frequencies). But other than that, the boundary conditions and aspect ratio basically determine the shape of the frequency response curve.
The part on the right depends only on the properties of the plate (E, rho, and nu), and its thickness and area. This combination of factors really just shifts the frequency response curve toward lower or higher frequencies. Increasing t or E shifts it to higher frequencies, and increasing the area or density shifts it to lower frequencies. And one interesting (and useful) result of this is that changes in any of these factors will have the same effect (shift) on any design, regardless of the boundary conditions. That is, for example, doubling the thickness of the panel (and keeping the boundary conditions the same) will double all the natural frequencies, that is , shift the frequency response curve higher by a factor of two, for any particular speaker design. And doubling the area should have exactly the opposite effect. That is, shift the frequency response down by half.
Eric
(PS, I sure hope I did the algebra right!)
You wrote:
Left to right: CCCC case - 700x300x3 panel - Q1 used to eliminate 'noise'
(1) Reducing E increases low freq range, no significant effect above 100Hz (for the chosen panel).
(2) Increasing density reduces mid to high level output in a non-linear manner
(3) As for (2) above - pale blue line overlays a SSSS case on the orange CCCC - indicates constraints principally affect low frequencies only.
(4) As for (3) above, red line overlays Q5 SSSS case on the pale blue SSSS Q1
Nice use of Pettals, Eucy. I decided to comment on this here, rather than in the other forum, I hope you don't mind.
One way to understand your observations even better is to look at the equation for the natural frequencies, like the one below. This is the eqn specifically for "simple" supports (SSSS), but it shares a lot of similarities with the equations for other boundary conditions.
The part on the left depends only on the boundary conditions and aspect ratio of the panel, and determines the relative positions along the frequency axis of all the natural frequencies. Hence, that part (along with the exciter position) largely determines the shape of the frequency response curve. That is, it determines where all the peaks and dips will happen relative to each other. Of course, the frequency response of the exciter itself will have some influence, especially at very low and very high frequencies, as will the exciter vc diameter and location of the coincidence frequency (at high frequencies). But other than that, the boundary conditions and aspect ratio basically determine the shape of the frequency response curve.
The part on the right depends only on the properties of the plate (E, rho, and nu), and its thickness and area. This combination of factors really just shifts the frequency response curve toward lower or higher frequencies. Increasing t or E shifts it to higher frequencies, and increasing the area or density shifts it to lower frequencies. And one interesting (and useful) result of this is that changes in any of these factors will have the same effect (shift) on any design, regardless of the boundary conditions. That is, for example, doubling the thickness of the panel (and keeping the boundary conditions the same) will double all the natural frequencies, that is , shift the frequency response curve higher by a factor of two, for any particular speaker design. And doubling the area should have exactly the opposite effect. That is, shift the frequency response down by half.
Eric
(PS, I sure hope I did the algebra right!)
@Veleric : the link works for you because you already got the authorization from Dave to download from there. It is the link for the .exe file (Windows), I use an other one for Linux (.install file)
Better is to start from Dave's page PETTaLS free.
Seems there is in addition a novelty, the install files are now stored in Github.
As you have opened the thread, Eric, I think you can update the 1st post.
Christian
Better is to start from Dave's page PETTaLS free.
Seems there is in addition a novelty, the install files are now stored in Github.
As you have opened the thread, Eric, I think you can update the 1st post.
Christian
I just made an update with the current (and fresh) version 1.2.1.
Note the version number is clearly visible in the installation file name and also in PETTaLS main screen => be sure to use the latest and refer to the version number for any feedback.
Christian
Note the version number is clearly visible in the installation file name and also in PETTaLS main screen => be sure to use the latest and refer to the version number for any feedback.
Christian
I think the link in the first post is fixed now. Thanks.
Eric
Eric
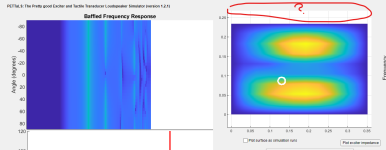
I just updated to 1.2.1. Glad to see the version number identified at the top. The surface velocity map now updates "manually" when I enter a number in the frequency field. Oddly, though, the plot gets a little bigger and covers the title of the plot. I'm guessing that's not supposed to happen.
Eric
Eric
I posted this earlier in the monster DML thread, but I thought I should add it here too. This video shows one of the really cool features of the Pettals simulation software. It is the Velocity Map which shows how the velocity profile of the panel changes as a function of frequency. It's very informative and fun to watch.
The simulation shown in the video runs from 20 Hz to 5,000 Hz. Note that it takes about 15 seconds before anything obvious happens so be patient. To me it looks like new antinodes are "born" at (or adjacent to) the exciter then move away as they "mature" and make room for a new antinode to be born.
Live Surface Velocity Map Video
The simulation shown in the video runs from 20 Hz to 5,000 Hz. Note that it takes about 15 seconds before anything obvious happens so be patient. To me it looks like new antinodes are "born" at (or adjacent to) the exciter then move away as they "mature" and make room for a new antinode to be born.
Live Surface Velocity Map Video
Yeah, we switched to github yesterday at the University's request. Since this isn't a code repo, we're just doing github "releases" - hopefully that will work for everyone.
I think I've fixed that in the newest version (which will be 1.2.2), along with the angular averaging problem eucy pointed out.
This seems right to me - I usually think of the relationship as: sensitivity is proportional to density, bandwidth is proportional to stiffness & density & size. It's complicated, though. I once gave a presentation to a bunch of elementary school students (and parents) about why cardboard sounds different from metal, and one parent said: "So what's the best sounding panel? Bigger panels always sound better?" When I answered "Well, it's complicated," the parents got mad at me and said I should come up with clearer rules. So I don't give that presentation anymore - now I talk about how loud volcanic eruptions are.
@Veleric I liked your experiment from the other thread where you halved the E and density a few times and saw an increase in the sensitivity while the bandwidth remained the same. But I thought to myself... there's got to be a limit to this - we can't just keep halving those parameters forever until we're able to get 1000 dB sensitivity! So I kept going... and sure enough, eventually the low frequency sensitivity drops off and even becomes lower than what it was in the first place. I tried this with both a free and fixed magnet and the results were essentially the same.
I tried a point force too, and it pointed out something else I need to fix - the point force is still seeing a voltage source rather than a current source for the panel mode component of its impedance. I'll fix that in the 1.2.2 release - I'm very interested to see if that allows the sensitivity to keep increasing forever (although it would be purely theoretical)!
I tried a point force too, and it pointed out something else I need to fix - the point force is still seeing a voltage source rather than a current source for the panel mode component of its impedance. I'll fix that in the 1.2.2 release - I'm very interested to see if that allows the sensitivity to keep increasing forever (although it would be purely theoretical)!
I'm interested to see that too, even if it is purely theoretical.
I'm out of action for a while folks.
Located just north of Brisbane and tropical cyclone Alfred has wrecked the area over the past few days
Today we've had about 300mm of rain, winds up to 150 km/hr in other areas, not near me.
Power is out for about 300,000 people including us.
Still raining, generator still running.
Life goes on.
Minor matters really, compared to other areas in this troubled world
Regards
Eucy
Here's a link to Dave's YouTube channel, which includes videos demonstrating the software. I also added this link to the first post in this thread.
PETTaLS Videos
PETTaLS Videos
I made some attempts to quantify Q for three different panel materials, using both the impedance test and tap test methods. The overall results look something like this:
PMMA (Acrylic) : ~20
EPS: ~70
Aluminum: ~1000
Are these correct? Not sure, but they were pretty consistent.
I performed all the tests with "free" panels, suspended from wires or pieces of tape located about 22% from either end. The long direction of the panel was horizontal. In the tap tests, the mic and tap locations where both at the center of the panel. I did two versions of the tap test, one with no exciter and a second with an exciter (FHE25-4, no wires) attached at the center. In the impedance test the exciter (VT25-4, wired) was placed at the center of the panel.
The three panels were:
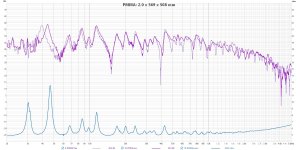
PMMA (Acrylic): 2 mm x 569 mm x 508 mm
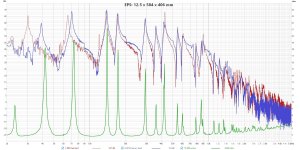
EPS: 12.5 mm x 584 mm x 406 mm
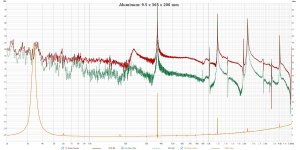
Aluminum: 9.5 mm x 365 mm x 206 mm
Of the three, only the EPS was the ideal size for this test. The PMMA was too large and thin, so the lowest modes were under 20 Hz, and not useful for measurements and also making identification of particular modes more difficult. The Aluminum was too small and thick, with the lowest frequency mode at nearly 400 Hz, so there were fewer modes within the measurement range than I would have preferred. But in the end, I don't think the results would have been much different with more "ideal" panels.
For the tap tests, I used the points 3dB below each peak SPL to determine the bandwidth for the Q calculation. For the impedance test, I use the points at 70.7% of the peak, referenced to the impedance curve baseline in the vicinity of the peak. I'm still not sure if these are the "correct" calculations.
The plots below show the three different measurements for each of the three materials, with the tap tests on top and the impedance test at the bottom. In each, the dotted curve is the tap test without the exciter attached. My calculated Q values are shown (in red) in the chart below the figures. There were a couple of outliers, which I highlighted in yellow, and which I did not include in my averages. I don't really have any explanations for the outliers. I attached also the REW mdat file. Please feel free to try your own evaluations of Q with this data or your own!
A couple of notes, observations and thoughts:
PMMA (Acrylic) : ~20
EPS: ~70
Aluminum: ~1000
Are these correct? Not sure, but they were pretty consistent.
I performed all the tests with "free" panels, suspended from wires or pieces of tape located about 22% from either end. The long direction of the panel was horizontal. In the tap tests, the mic and tap locations where both at the center of the panel. I did two versions of the tap test, one with no exciter and a second with an exciter (FHE25-4, no wires) attached at the center. In the impedance test the exciter (VT25-4, wired) was placed at the center of the panel.
The three panels were:
PMMA (Acrylic): 2 mm x 569 mm x 508 mm
EPS: 12.5 mm x 584 mm x 406 mm
Aluminum: 9.5 mm x 365 mm x 206 mm
Of the three, only the EPS was the ideal size for this test. The PMMA was too large and thin, so the lowest modes were under 20 Hz, and not useful for measurements and also making identification of particular modes more difficult. The Aluminum was too small and thick, with the lowest frequency mode at nearly 400 Hz, so there were fewer modes within the measurement range than I would have preferred. But in the end, I don't think the results would have been much different with more "ideal" panels.
For the tap tests, I used the points 3dB below each peak SPL to determine the bandwidth for the Q calculation. For the impedance test, I use the points at 70.7% of the peak, referenced to the impedance curve baseline in the vicinity of the peak. I'm still not sure if these are the "correct" calculations.
The plots below show the three different measurements for each of the three materials, with the tap tests on top and the impedance test at the bottom. In each, the dotted curve is the tap test without the exciter attached. My calculated Q values are shown (in red) in the chart below the figures. There were a couple of outliers, which I highlighted in yellow, and which I did not include in my averages. I don't really have any explanations for the outliers. I attached also the REW mdat file. Please feel free to try your own evaluations of Q with this data or your own!
A couple of notes, observations and thoughts:
- no surprise, but the differences between the three materials are massive!
- the Q's are quite a bit higher than what Dave has currently in Pettals.
- the addition of the exciter doesn't really change the apparent Q very much, if at all. The addition of the exciter does push the lowest frequency peaks a bit higher, but seems not to change the sharpness of the peaks.
- the results calculated by the tap and impedance methods are surprisingly similar, particularly for the PMMA and EPS.
- For the EPS and Aluminum panels, pretty much all the peaks in the tap and impedance test represent modes where the center is an antinode. For the PMMA, I think some of the modes excited don't have an antinode at the center, but were excited anyway. Interestingly, the Q values I calculated for the PMMA were remarkably consistent in spite of this.
Here are the results with the point force. It does increase up to a point, then losses from acoustic loading take over. So it can't keep going forever!
Sorry to hear that! I've been supporting a Queensland-based podcast for years and the host is sending updates as well. Hope the flooding stops soon. I used to live in Adelaide, so I've got a special affinity for Australia!
@Veleric
Hello Eric,
About Q measurement...
Below is an impedance measurement of a DAEX25FHE alone. Orange is the exciter alone (no panel, no added mass), green is the exciter with a 7.8g mass added (this in order to extract the exciter parameters with REW)
Near a mode, a panel can be modeled by its equivalent mass/spring/damper network as any loudspeaker (or exciter alone) at its resonance.
The damping is Rms
What REW tells here is the Q of the nominal mechanical system is 32. fs (free) = 267Hz Z = 210Ohm
Following
With a mass added (only Mmms changedn Rms and Cms are the same) fs (mass added) = 111Hz, Z = 44Ohm and a new Qms = 77 (changes like sqrt(newMms/Mms) at the opposite of fs)
with delta f = fs / Q, it comes delta f (free) = 8Hz, delta f (mass added) = 1.4Hz and the according impedance 155Ohm and 39Ohms
So a ratio of impedance of 0,74 and 0,98...? What's wrong?
Sorry for the digression, in fact before this I was thinking to your post and the limitation of what we could measure with the impedance
With the value of Q you shown for aluminum, I wonder if we have the required precision in frequency but mainly I have the feeling there is a limit due to the exciter damping. Could we really observe very high Q when the exciter brings its own damping?
Hello Eric,
About Q measurement...
Below is an impedance measurement of a DAEX25FHE alone. Orange is the exciter alone (no panel, no added mass), green is the exciter with a 7.8g mass added (this in order to extract the exciter parameters with REW)
Near a mode, a panel can be modeled by its equivalent mass/spring/damper network as any loudspeaker (or exciter alone) at its resonance.
The damping is Rms
What REW tells here is the Q of the nominal mechanical system is 32. fs (free) = 267Hz Z = 210Ohm
Following
With a mass added (only Mmms changedn Rms and Cms are the same) fs (mass added) = 111Hz, Z = 44Ohm and a new Qms = 77 (changes like sqrt(newMms/Mms) at the opposite of fs)
with delta f = fs / Q, it comes delta f (free) = 8Hz, delta f (mass added) = 1.4Hz and the according impedance 155Ohm and 39Ohms
So a ratio of impedance of 0,74 and 0,98...? What's wrong?
Sorry for the digression, in fact before this I was thinking to your post and the limitation of what we could measure with the impedance
With the value of Q you shown for aluminum, I wonder if we have the required precision in frequency but mainly I have the feeling there is a limit due to the exciter damping. Could we really observe very high Q when the exciter brings its own damping?