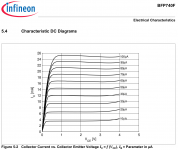
Well, looking at the plot in post #30, it is not so much "noise" (these are 140dB parts) as simple lack of data (I posited wrong). In the low Vce area there's only 4 or 5 points. Is that typical, hard-coded, or user-set? Can we get some more points in there? In SPICE I would plot this area with 10mV steps.
When you plot Early voltage vs Vce, any noise in the curves is amplified. At high Early voltages smoothing is usually not enough. In theory one could keep repeating the measurement and averaging the result until noise was low enough or ADC/DAC nonlinearity was too high, but I've never seen this feature in a curve tracer.
PyPSUcurvetrace will allow you to do this (yes, PyPSUcurvetrace is a different beast than the tracer discussed here).one could keep repeating the measurement and averaging the result until noise was low enough or ADC/DAC nonlinearity was too high, but I've never seen this feature in a curve tracer.
Look at the bottom curve (Ib = 10uA). You can see that the Vce stepping is extremely coarse, something like 8 steps per volt (125 mV per step).
It appears to be a very low voltage device, probably intended for RF applications. It begins to misbehave around Vce>3.7 volts. Which means the curve trace hardware and plot should have stepped Vce at 5 millivolts per step (200 steps per volt)!! Ugh.
It appears to be a very low voltage device, probably intended for RF applications. It begins to misbehave around Vce>3.7 volts. Which means the curve trace hardware and plot should have stepped Vce at 5 millivolts per step (200 steps per volt)!! Ugh.
This is an unfair statement because you don't even have used the tracer.PyPSUcurvetrace will allow you to do this (yes, PyPSUcurvetrace is a different beast than the tracer discussed here).
Since begining, compared with other tracers, the author of iTracer makes more efforts on its transistor batch <matching> and <pairing> ability.
Theses efforts are mainly shown on the software aspect.
For example, how do we gonna do if we need to identify matched pairs from a batch of 100 transistors?
For sure we can use curve tracers and plot traces of these 100 transistors, then compare the curves one by one.
If the plotted curves are close or overlapping, one may think: oh! These 2 transistors are the matched pair! Job done!
However, what we are thinking about is how close is enough to say they are matched?
Two derivative question raised:
1. Can we quantify "close"?
2. Is there better way for quicker, automatic measuring?
Hence, mathematical models and algorithms are developped for this tracer project:
1. The iTracer can measure a batch of DUTs up 8 pcs at once, automatically(by swithing relays).
2. After measurement and proccessed, every DUTs can be quantified based on their own curves.
3.With quantified DUTs, the software can rapidly and accurately choose and select matched pairs, and tell you how similar/close they are by numbers!
Ex.
Matched Pair No.20, Similarity=96%
Matched Pair No.5, Similarity=94%
And of course, you can make your own definition of "similar", enter a number like 0.8 and the system will tell you all the pairs that are 80% similar with each other in this batch, easy and simple!
Theses efforts are mainly shown on the software aspect.
For example, how do we gonna do if we need to identify matched pairs from a batch of 100 transistors?
For sure we can use curve tracers and plot traces of these 100 transistors, then compare the curves one by one.
If the plotted curves are close or overlapping, one may think: oh! These 2 transistors are the matched pair! Job done!
However, what we are thinking about is how close is enough to say they are matched?
Two derivative question raised:
1. Can we quantify "close"?
2. Is there better way for quicker, automatic measuring?
Hence, mathematical models and algorithms are developped for this tracer project:
1. The iTracer can measure a batch of DUTs up 8 pcs at once, automatically(by swithing relays).
2. After measurement and proccessed, every DUTs can be quantified based on their own curves.
3.With quantified DUTs, the software can rapidly and accurately choose and select matched pairs, and tell you how similar/close they are by numbers!
Ex.
Matched Pair No.20, Similarity=96%
Matched Pair No.5, Similarity=94%
And of course, you can make your own definition of "similar", enter a number like 0.8 and the system will tell you all the pairs that are 80% similar with each other in this batch, easy and simple!
Last edited:
Unfair? I dont get that. All I wrote is that PyPSUcurvetrace will happily do the averaging. This was in response to the previous post saying that he has not seen a curve tracer that will do any averaging.This is an unfair statement because you don't even have used the tracer.
Hi,Unfair? I dont get that. All I wrote is that PyPSUcurvetrace will happily do the averaging. This was in response to the previous post saying that he has not seen a curve tracer that will do any averaging.
I sincerely appologize to you and my post.
I was posting reply as I was focusing on "PyPSUcurvetrace is a different beast than the tracer discussed here", and took it on the wrong way, misunderstand that you are implying
iTracer is second to PyPSUcurvetrace.
I am sorry and again I appologize for my words.
Also, thank you for remainding me for my being misunderstanding.
Sincerely,
Jensen
Oh I see! All good 🙂Hi,
I sincerely appologize to you and my post.
I was posting reply as I was focusing on "PyPSUcurvetrace is a different beast than the tracer discussed here", and took it on the wrong way, misunderstand that you are implying
iTracer is second to PyPSUcurvetrace.
I am sorry and again I appologize for my words.
Also, thank you for remainding me for my being misunderstanding.
Sincerely,
Jensen
By "different brast" I was trying to say that the two tracer systems work in very different ways.
Thank you 🙂Oh I see! All good 🙂
By "different brast" I was trying to say that the two tracer systems work in very different ways.
I am glad to dicuss such detailed things with you guys.
Hi, what do you think about this?
(Maybe this help to solve the prolbem ....a bit?)
Better Modeling of β vs. IC At High IC
The article states that the SPICE IKF parameter specifies the value of IC above which the log slope of IC vs. VBE becomes smaller, but that the slope itself in the high-current region is fixed. While this is true for the standard Gummel-Poon model, PSPICE added a new parameter called NK which allows for this log slope to be specified. LTspice supports NK as well, though it's not documented. Recent experimentation with NK shows it to be extremely useful, even mandatory, for getting a good match of simulated and measured β at large IC values. The models developed in the article required sacrificing accuracy of simulated β in the high-current region to get the best possible accuracy at more typical currents. This compromise is no longer necessary when NK is used.Ref: https://www.andyc.diy-audio-engineering.org/spice-models/index.html
Math issues are chained by one another and another, authough I did not participate in ther core development of iTracer's brain.Thank you for that link!!
By reading related materials ( I have to do so that I can discuss with the author "ss" on the same level),
I think tracing is something like "scanning" transistors, realize "his/her" charateristcs by curves.
However, One single curve or one single dagram are not enough for realizing he or she.
In attempts to better know our transistor friends, we conduct more and more curve plottings from other aspects to describe this friend.
And here one name cannot be neglected, the SPICE(Simulation Program with Integrated Circuit Emphasis).
Those guys in UC Berkeley are so super ambitious, they want to describe/quantify transistors by knowing their transistors' friends in every aspects from any point view. That said, their goal is to make sure that modelled transistors react and behave exactly indentical to those in real world.
This way, commonly known as SPICE by Berkeley some 50 years ago, still updating and still plays super important role.
The SPICE modelling involves physics, mathematics so profesionally, making it became the king of semidonductor modelling, later it became a universal langual while devices simulation are needded. Modelled devices improve software's capability of simulation and analysis, nowadays it's called EDA, that perform electronic simulations before realistic experiments, which greatly enhances cost-effectiveness and reduces developing time and cost.
You will run into problems using IKF to model beta-droop in all transistors. Look at my Sanken spice model threads. Virtually all of the beta droop in those transistors was caused by quasi-saturation, and fitting the curve with IKF actually caused invalid results. I don't know if this has been documented anywhere, I seem to be the only person here to point it out.
Yes, so from the very beginning, the idea of "comparing DUTs by SPICE" had been ruled out quickly. Too complex, and too detailed.You will run into problems using IKF to model beta-droop in all transistors. Look at my Sanken spice model threads. Virtually all of the beta droop in those transistors was caused by quasi-saturation, and fitting the curve with IKF actually caused invalid results. I don't know if this has been documented anywhere, I seem to be the only person here to point it out.
We adopted a new algorithm to process DUTs with matching emphasis.
oh, wait a sec, I just came out with:
Simulation Aprroximation with Matching Emphasis, SAME
We will talk about SAME with more detail soon, the way we avoid the "SPICE trap" ,
yet still very capable to distinguish the differences in a quantified, scientific approach.
You could probably write PhD thesis about different transistor matching approaches. However, "matching" parts and expressing their "overall goodness of match" by a simple number makes no sense if you ask me. It is better to first understand the needs of a given circuit with respect to characteristic(s) that need to be matched. Do parts need to be matched for gain? DC operating point? (Non)linearity? Etc.? Only once you know what you are looking for, you can start to analyze the curves and match the relevant parameters.
You could probably write PhD thesis about different transistor matching approaches. However, "matching" parts and expressing their "overall goodness of match" by a simple number makes no sense if you ask me. It is better to first understand the needs of a given circuit with respect to characteristic(s) that need to be matched. Do parts need to be matched for gain? DC operating point? (Non)linearity? Etc.? Only once you know what you are looking for, you can start to analyze the curves and match the relevant parameters.
Thank you for your poins.
Indeed, the idea of "matching" is not a easy thing to explain.
Simply speaking, our idea is to made "matching" more than oberving curves but less than involving something like statistics, because it's hobbyist-oriented; yet there is gonna be a manual that explains the details (publish later).
But I will brief talk about this here, and I have to clarify that it not just a simple number that decides the "overall goodness of match", or perhaps "similarity" in the following.
We propose another way to represent curves of transistor, and also another way to represent the extent of similar.
In the chater of the manual:
.......Take adventage of Curve Fitting Function
More ideally, it is better to develop mathematical models of curves, by using fitting functions to describe curves, then calculate similarity based on them.
Utilizing SPICE model is an excellent way to describe semiconductors’ characteristics. These models are based on semiconductor’s physical properties, and there are too many parameters that are hard to get. SPICE is unnecessarily too complex for hobbyist-grade matching.
Alternatively, we choose another approach.
The curve fitting function could be used to describe curves.
Both input and output transfer function can be curve-fitted. Mathematically, by means of parameterizing, the <characteristic vectors> can be made on the basis of fitting functions. The distance between vectors could be seen as the similarity of different curves, with weightings and some adjustment.
Estimating Function Similarity
Once fitting functions are established, similarity could therefore be calculated based on them.
Calculating similarity basically consists of three steps:Establish Fitting Function’s specific “vector”
Use any measured points (x, y) on curves, one can thereby solve the function to get corresponding constants.
Take BJT for example, the BJT output function can be desbribed as:Ic=A−Ke^ (−Buce)+K1uce|Ib
We got 4 coefficients A, K, B, K1 in the formula, which can be obtained by solving the function using measured points, (Ic, uce) in this case.
Once constants of fitting functions are available,
we propose to define a vector called “characteristic vector”, <A,K,B,K1>|Ib in this case, which can be used to represent the curves.
Establishing Similarity
The components of the “characteristic vector”, <A,K,B,K1>, paly different roles on their own to influent the curves.
In short, by establishing a 4-Dimension coordinate, similarity could be seen as the distance of 2 points in the dimesion (sort of),computed by averaging and weighting on the basis of <A,K,B,K1>.
...................................................to be continued.
- Home
- Design & Build
- Equipment & Tools
- New Tracer is coming