I would assume that the location of the mike at any position in space, either over or under, could be used to change the sound.
Genearally it does, often quite dramatically. But, orthogonal to a blurry/focused axis direction (for what I would call blurry sound -- which usually happens after the mic, at least if the mic is a good one).
EDIT: There are reasonably other categories of things that might be considering as blurring. Room reflections, masking noises, HF attenuation with distance, unsuitable mics, etc.
Last edited:
Its more complicated than that, usually more than one underlying cause.
Yes, complicated, any better orifices where to ahem.. hide the mike? 😉
It also shows that an amplitude modulation using two in band frequencies (2.5 k and 20) will generate a signal at 22.5K.
I keep not quite understanding the point, if you modulate (fully) a 20k sine with a 2.5k sine there is no 20k sine. If you filter away the 22.5k sine the 17.5k sine is all that is left. There is no 20k in 17.5k out.
KSTR explained what was happening very clearly I think?At least KSTR tried it, he provided the exact same results as Hans.
I keep not quite understanding the point, if you modulate (fully) a 20k sine with a 2.5k sine there is no 20k sine. If you filter away the 22.5k sine the 17.5k sine is all that is left. There is no 20k in 17.5k out.
you have to argue with whever defined that trig identity. I honestly did not expect the result Hans provided, and in digging very far, found the math.
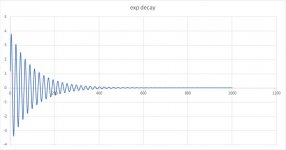
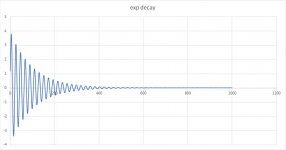
I just updated the wave I was trying for, this is a bell hit with exponential decay. The leading edge violates ny-baby, the start of the trail edge may or may not at the start.
If we were to raise the fundamental frequency and increase the decay, I bet your gibbs envelope through a filter would show huge at the start, and tailor off much faster than the actual envelope as the envelope slope gets less steep.
jn
Attachments
Last edited:
Yah, and he also said the two waveforms were identical. Which they very clearly are not.KSTR explained what was happening very clearly I think?
jn
42 = (-80538738812075974)**3 +
(80435758145817515)**3 +
(12602123297335631)**3
I have recently found that it is very efficient and satisfying to read only your comments.
😛
Here is my attempt at calculating the addition and multiplication of the signals quoted by jneutron.
The upper plot is the addition of the 17.5 and 22.5 kHz sines, the lower one is the multiplication of a 20 kHz sine with a 2.5 kHz cosine.
All signals have a sampling rate of 44.1 kHz.
There is a factor of two difference in the amplitudes, the lower plot result agrees with "Signals and Systems", Oppenheim et al., 1986.
Is anything missing in my calculations?
The upper plot is the addition of the 17.5 and 22.5 kHz sines, the lower one is the multiplication of a 20 kHz sine with a 2.5 kHz cosine.
All signals have a sampling rate of 44.1 kHz.
There is a factor of two difference in the amplitudes, the lower plot result agrees with "Signals and Systems", Oppenheim et al., 1986.
Is anything missing in my calculations?
Attachments
Nope. The factor of two is actually built into the identity. You did it perfect.There is a factor of two difference in the amplitudes, the lower plot result agrees with "Signals and Systems", Oppenheim et al., 1986.
Is anything missing in my calculations?
jn
This was the explanation I was thinking of, particularly the last sentence?Yah, and he also said the two waveforms were identical. Which they very clearly are not.
It isn't, and any filter cannot change that. You are still mistaking the peak magnitude point of the filtered response as the point where the carrier freq is situated, which is only true when no additional EQ is present, obviously. With EQ, the peak point in the spectrum does shift but the carrier and the sideband frequencies are not changed. In a single cycle of raised cosine window the components have widespread leakage, in the periodic equivalent we see distinct lines at 20k carrier and 15/25kHz lower sidebands and that picture doesn't change when additional EQ is applied to this.
I’ve been following this thread for months, and last few weeks are like a soap opera. I’m sure there must be many lurkers desperate to know the truth! There are clearly some very knowledgeable and experienced people on this thread. Could any of you recommend a text book on DSP for an engineer, but not one with a background DSP? I’ll read it and then see if this debate has concluded in the meantime! Genuine request ��. Thank you.
Matt, on 100% modulated signal, there no longer present any carrier frequency component. When upper sideband is filtered out only lower sideband is left. It is true that carrier frequency does not change but there is no more carrier frequency component to show.This was the explanation I was thinking of, particularly the last sentence?
Most probably even less than a blip of the carrier frequency component was left on Hans' example. 😀
If this debate is basically about attack of envelopes causing sidebands to be created I'm yet to be convinced.I’ll read it and then see if this debate has concluded in the meantime!
Ironically both Hans and KSTR have given up, can't say I blame them, shame thoughMost probably even less than a blip of the carrier frequency component was left on Hans' example. 😀
Last edited:
If this debate is basically about attack of envelopes causing sidebands to be created I'm yet to be convinced.
Which is quite alright, I wouldn't want it any other way.
jn
Bingo! That's the Jn's 20kHz in -> 17.5 or whatever kHz out. 100% modulation! 😀
Umm, now you get it??😀
Even at lower modulation percentage, the sidebands exist at the modulation frequency + carrier.
Look at the exponential envelope. Ignore the leading edge, we all understand that.. Lobe to lobe of the hf signal is dropping severely at first, then easing up as it tails. That initial envelope steepness is high frequency envelope modulation that will sideband..as the steepness declines, the sidebands pull in to the carrier. As they pull in, they may cross the frequency threshold where the full content gets through, where the initial sidebands were cut out.
jn
Attachments
No, not in the way you are presenting it. 100% modulation? In music? Where? When?Umm, now you get it??😀
Oh, really? What a revelation. Wasn't there a 50% modulation sidebands in my FFT measurements several pages back?Even at lower modulation percentage, the sidebands exist at the modulation frequency + carrier.
Oops, sorry, I forgot, Fourrier is cr@p 😡
It is only fair to direct the question to the one bringing in that particular example on #34414. 🙂No, not in the way you are presenting it. 100% modulation? In music? Where? When?...
- Status
- Not open for further replies.
- Home
- Member Areas
- The Lounge
- John Curl's Blowtorch preamplifier part III