Hello Kaspar,
snip
Have you ever heard about Paint Shop Pro?
No, but know!😀
snip
LTspice lacks some options. The fact that you can't import data from an old simulation is one.
You can, try "open" "all files", but You cannot put them together.
snip
I also bothers me that you can't copy from one schematic to another.
No problem: From the Yahoo-group "FAQ":
Q: How do you copy and paste between schematics?
A: Click on "Copy" in the tool bar. Select what you want to copy.
Make the other schematic active and then click on "paste" in the tool bar."
Q: How do I copy and paste between symbols in the symbol editor?
A: It is not possible to use copy and paste in the symbol editor.
Symbol files are ASCII-text. Merge the text as described in message 7201.
snip
I prefer Orcad PSpice for simulations.
Huh, please not for me!🙂
snip
You're right that simulation is slow and then it's not accurate even at small time steps. However you can do a relative comparison of the distortion, I think.
I agree!
snip
When I add additionally feedback arround a switching amplifier, I place a sinus generator at the output and mesure how well it's attenuated compared to before adding feedback. In that way I can mesure the relative improvement (you really need a small time step and a long simulation time to see the difference in THD).
Yes, to inject a current in the output is useful. In this case often the amp internally don´t need to do big voltage excursions.
So I normally use this test "later".
snip
Often things turn out differently than I'd expected.
How true
snip
From observation it seams that it's the ratio between the openloop gain at the oscillation frequency and the openloop gain at a given audible frequency that determines the attenuation of the sinus disturbance.
I simply don´t know!
My "working-style" is more like the experimenter : I try in a short time many possibilities and observe "what happens" and get so a better idea how it works. So, with pwm-amps in a simulator I get really a problem because I had to wait too long for that "what happens"
For "learning" I download from the Yahoo-group "LTSputil" This programm can merge e.g. FFT files. It "costs" me hours to learn to use it, but at least I use it to compare what "happens" when I put a lowpass in one leg of the current-fb.
I wish all a nice day, I had to continue my work (for money....I will hope😀 )
Regards
Heinz!
snip
Have you ever heard about Paint Shop Pro?
No, but know!😀
snip
LTspice lacks some options. The fact that you can't import data from an old simulation is one.
You can, try "open" "all files", but You cannot put them together.
snip
I also bothers me that you can't copy from one schematic to another.
No problem: From the Yahoo-group "FAQ":
Q: How do you copy and paste between schematics?
A: Click on "Copy" in the tool bar. Select what you want to copy.
Make the other schematic active and then click on "paste" in the tool bar."
Q: How do I copy and paste between symbols in the symbol editor?
A: It is not possible to use copy and paste in the symbol editor.
Symbol files are ASCII-text. Merge the text as described in message 7201.
snip
I prefer Orcad PSpice for simulations.
Huh, please not for me!🙂
snip
You're right that simulation is slow and then it's not accurate even at small time steps. However you can do a relative comparison of the distortion, I think.
I agree!
snip
When I add additionally feedback arround a switching amplifier, I place a sinus generator at the output and mesure how well it's attenuated compared to before adding feedback. In that way I can mesure the relative improvement (you really need a small time step and a long simulation time to see the difference in THD).
Yes, to inject a current in the output is useful. In this case often the amp internally don´t need to do big voltage excursions.
So I normally use this test "later".
snip
Often things turn out differently than I'd expected.
How true
snip
From observation it seams that it's the ratio between the openloop gain at the oscillation frequency and the openloop gain at a given audible frequency that determines the attenuation of the sinus disturbance.
I simply don´t know!
My "working-style" is more like the experimenter : I try in a short time many possibilities and observe "what happens" and get so a better idea how it works. So, with pwm-amps in a simulator I get really a problem because I had to wait too long for that "what happens"
For "learning" I download from the Yahoo-group "LTSputil" This programm can merge e.g. FFT files. It "costs" me hours to learn to use it, but at least I use it to compare what "happens" when I put a lowpass in one leg of the current-fb.
I wish all a nice day, I had to continue my work (for money....I will hope😀 )
Regards
Heinz!
Attachments
Excuse me a moment while I climb onto my LTspice box. 
Ah, there.
Are you attempting to measure THD in a class-d amplifier simulation in LTspice? In principle, LTspice’s FFT or .four command should be just the right tools with which to make your THD + noise measurement. In practice, simulators (even LTspice) are hard pressed to capture the exact timing of the switching edges of a class-d amplifier. To be interesting, a THD measurement must resolve a fraction of a percent (say, a few parts per hundred thousand). Couple this with a typical low level THD test signal that is only a fraction of the supply voltage (perhaps one volt verses one hundred) and the simulator's variable time step algorithm must calculate the exact moment of switching to within around one part per million. At typical class-d switching frequencies, that implies timing accuracy to within a few picoseconds. This can be a challenge, even when using all of LTspice’s many tricks and enhancements.
As an example, let’s say your latest class-d design is finally simulating like a dream and you now wish to run and compare FFT and .four THD measurements out through 20kHz using a 1kHz source.
First you will want to label the input and output nodes (say, “in” and “out”) and connect a 1kHz sine source to the input. The required amplitude will depend on amplifier gain and desired output level for the THD measurement (1 volt ac on the output is a good choice for starters).
.param gain=10 ; just an example – you specify
Vin in 0 sine(0 {1/gain} 1kHz) ; dc level set to zero
The Fourier (.four) analysis operates on the specified data source to extract the specified number of harmonics of the specified frequency over the time interval from the end of the simulation to exactly the specified number of periods before the end. The harmonics and periods default to 9 and 1 respectively, but you’ll want to set up different numbers in order to get the desired results. Since the base frequency is 1kHz, you’ll need to see at least 20 harmonics and you’ll want to measure over at least 16 cycles for good resolution.
.four 1k 20 16 V(out) ; frequency, harmonics, periods, data source
Next, for best accuracy and dynamic range, you’ll want to turn off compression of saved data.
.options numdgt=16 ; no data digit compression
.options plotwinsize=0 ; no data time compression
Now that you’ve opened up the data spigot, you may wish to only save the most interesting data to avoid flooding your hard drive.
.save V(out) ; see Help file for more options
When you set up the FFT, you select the time period and number of data points to use. Then LTspice gives you a plot that spans the appropriate frequency range given that input. Whether or not you have aliasing artifacts and “noise” depends on whether or not you set up the FFT appropriately and gave it a good data set to work with. The SPICE engine is completely oblivious to the needs of whatever FFT you might decide run on the output data.
Keep in mind that an FFT is an offline, or post, analysis. For an FFT, the existing output data is interpolated onto data points equally spaced in time. You will help LTspice control this interpolation in the FFT dialog by choosing the time range, the number of data points, etc. You also control the accuracy of your FFT by stipulating the maximum time step of the simulation data and the data compression. Best FFT data is had with no data compression and when the total number of transient time steps matches the number of FFT time point specified.
.param freq=1k nfft=32768 ; you supply these parameters
.param Tdata=10/freq ; depends on initial settling time required
.param dt=1/freq/nfft ; calculated based on your inputs above
.param Tend=Tdata+dt+16/freq ; calculated to yield 16 cycles of data
.tran {dt} {Tend} {Tdata} {dt} uic ; use initial conditions for class-d
Be sure to initialize the circuit closely as possible to its steady state. This can save much running time, as a startup transient has to settle to a very high precision before .four or an FFT should be applied. Specify initial voltages for capacitors and currents for inductors by entering ic=<data> right after the component’s value (e.g. “1uF ic=3V”) or by ctrl-right clicking over the component with the mouse and entering the ic statement in the component’s Value2 field.
A couple of other options are worth a mention.
.options reltol=.0001 ; *may* help increase accuracy of FFT
.options trtol=7 ; using 3 to 7 *may* increase speed
.options nomarch ; runs faster (no waveforms) but blind
If you run into singular matrix issues or just want to increase the SPICE engine’s numerical dynamic range, you may try selecting the Alternate Solver (via the SPICE tab of LTspice’s Control Panel). It runs at about half normal simulation speed but 1000x more accurately. Note that the normal solver usually will be just as accurate as the alternate solver since round-off error in the sparse matrix is rarely the limiting factor to simulation accuracy (always test this for a given FFT).
Regards -- analogspiceman
PS: Curly braces {} where shown above are required by LTspice.
Ah, there.Are you attempting to measure THD in a class-d amplifier simulation in LTspice? In principle, LTspice’s FFT or .four command should be just the right tools with which to make your THD + noise measurement. In practice, simulators (even LTspice) are hard pressed to capture the exact timing of the switching edges of a class-d amplifier. To be interesting, a THD measurement must resolve a fraction of a percent (say, a few parts per hundred thousand). Couple this with a typical low level THD test signal that is only a fraction of the supply voltage (perhaps one volt verses one hundred) and the simulator's variable time step algorithm must calculate the exact moment of switching to within around one part per million. At typical class-d switching frequencies, that implies timing accuracy to within a few picoseconds. This can be a challenge, even when using all of LTspice’s many tricks and enhancements.
As an example, let’s say your latest class-d design is finally simulating like a dream and you now wish to run and compare FFT and .four THD measurements out through 20kHz using a 1kHz source.
First you will want to label the input and output nodes (say, “in” and “out”) and connect a 1kHz sine source to the input. The required amplitude will depend on amplifier gain and desired output level for the THD measurement (1 volt ac on the output is a good choice for starters).
.param gain=10 ; just an example – you specify
Vin in 0 sine(0 {1/gain} 1kHz) ; dc level set to zero
The Fourier (.four) analysis operates on the specified data source to extract the specified number of harmonics of the specified frequency over the time interval from the end of the simulation to exactly the specified number of periods before the end. The harmonics and periods default to 9 and 1 respectively, but you’ll want to set up different numbers in order to get the desired results. Since the base frequency is 1kHz, you’ll need to see at least 20 harmonics and you’ll want to measure over at least 16 cycles for good resolution.
.four 1k 20 16 V(out) ; frequency, harmonics, periods, data source
Next, for best accuracy and dynamic range, you’ll want to turn off compression of saved data.
.options numdgt=16 ; no data digit compression
.options plotwinsize=0 ; no data time compression
Now that you’ve opened up the data spigot, you may wish to only save the most interesting data to avoid flooding your hard drive.
.save V(out) ; see Help file for more options
When you set up the FFT, you select the time period and number of data points to use. Then LTspice gives you a plot that spans the appropriate frequency range given that input. Whether or not you have aliasing artifacts and “noise” depends on whether or not you set up the FFT appropriately and gave it a good data set to work with. The SPICE engine is completely oblivious to the needs of whatever FFT you might decide run on the output data.
Keep in mind that an FFT is an offline, or post, analysis. For an FFT, the existing output data is interpolated onto data points equally spaced in time. You will help LTspice control this interpolation in the FFT dialog by choosing the time range, the number of data points, etc. You also control the accuracy of your FFT by stipulating the maximum time step of the simulation data and the data compression. Best FFT data is had with no data compression and when the total number of transient time steps matches the number of FFT time point specified.
.param freq=1k nfft=32768 ; you supply these parameters
.param Tdata=10/freq ; depends on initial settling time required
.param dt=1/freq/nfft ; calculated based on your inputs above
.param Tend=Tdata+dt+16/freq ; calculated to yield 16 cycles of data
.tran {dt} {Tend} {Tdata} {dt} uic ; use initial conditions for class-d
Be sure to initialize the circuit closely as possible to its steady state. This can save much running time, as a startup transient has to settle to a very high precision before .four or an FFT should be applied. Specify initial voltages for capacitors and currents for inductors by entering ic=<data> right after the component’s value (e.g. “1uF ic=3V”) or by ctrl-right clicking over the component with the mouse and entering the ic statement in the component’s Value2 field.
A couple of other options are worth a mention.
.options reltol=.0001 ; *may* help increase accuracy of FFT
.options trtol=7 ; using 3 to 7 *may* increase speed
.options nomarch ; runs faster (no waveforms) but blind
If you run into singular matrix issues or just want to increase the SPICE engine’s numerical dynamic range, you may try selecting the Alternate Solver (via the SPICE tab of LTspice’s Control Panel). It runs at about half normal simulation speed but 1000x more accurately. Note that the normal solver usually will be just as accurate as the alternate solver since round-off error in the sparse matrix is rarely the limiting factor to simulation accuracy (always test this for a given FFT).
Regards -- analogspiceman
PS: Curly braces {} where shown above are required by LTspice.
Hello analogspiceman,
puuh, I had to become very old to learn this all!😀
Thanks a lot for this extensive lesson!
Plenty off this stuff I see before at the Yahoo-group, but it´s hard to remember where to find or to search after because it´s not all keep together.
Now here You join all together, don´t forget to put it to the FAQ´s!
I had to print it out, to read it often till I understand all, one of my other problems is english!
Some time ago I try some experiments with my old simulator to modulate the hysterese of this kind of pwm-modulator, but the results seemed to be not solid, so I gave it up.
Sometimes ore often the use of a realtime simulator works better....where is my solderind iron?😉
Thank You again,
Regards
Heinz!
puuh, I had to become very old to learn this all!😀
Thanks a lot for this extensive lesson!
Plenty off this stuff I see before at the Yahoo-group, but it´s hard to remember where to find or to search after because it´s not all keep together.
Now here You join all together, don´t forget to put it to the FAQ´s!
I had to print it out, to read it often till I understand all, one of my other problems is english!
Some time ago I try some experiments with my old simulator to modulate the hysterese of this kind of pwm-modulator, but the results seemed to be not solid, so I gave it up.
Sometimes ore often the use of a realtime simulator works better....where is my solderind iron?😉
Thank You again,
Regards
Heinz!
Analogspiceman,
I really like it when you soap box!
I've gotten in the habit of running the fft on a 2^n cycles.
Like if its 1kHz excitation, I'll run the FFT for 256 or 1024mS.
Is that required?
Seems like it works good, but I've never really compared alot.
I just thought it would give less spilling, or blurring of the harmonic spikes.
Also, has anyone looked at, gee, don't really know what to call it, but I think it would be called current mode hysteretic.
Its similar to the scheme for desktop CPU power that's floated to the top for its superior transient response.
I haven't looked at it for a long time, and don't have access to the Intel book anymore, but it was very fast, and pretty simple as I recall.
Ever heard of something similar for class D?
Best REgards,
Mike
Proud owner of two brand new UcD's today 😀
I really like it when you soap box!
I've gotten in the habit of running the fft on a 2^n cycles.
Like if its 1kHz excitation, I'll run the FFT for 256 or 1024mS.
Is that required?
Seems like it works good, but I've never really compared alot.
I just thought it would give less spilling, or blurring of the harmonic spikes.
Also, has anyone looked at, gee, don't really know what to call it, but I think it would be called current mode hysteretic.
Its similar to the scheme for desktop CPU power that's floated to the top for its superior transient response.
I haven't looked at it for a long time, and don't have access to the Intel book anymore, but it was very fast, and pretty simple as I recall.
Ever heard of something similar for class D?
Best REgards,
Mike
Proud owner of two brand new UcD's today 😀
I guess you haven't read very much of this thread. 🙂
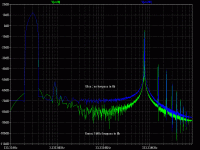
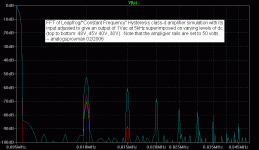
That was very much a topic of discussion. Thanks to an idea I got over on the LTspice Yahoo group, I've gotten better at setting up simulations for maximum FFT and DFT (.four) resolution and have been able to compare the distortion performance of an ideal UcD design with a smallish 5kHz test signal while under varying degrees of dc bias (none to nearly railed) against a hysteretic, constant frequency ideal leapfrog (current mode control) design under the same conditions.
The UcD seems to suffer increasing distortion, including nasty even harmonics, as the dc level of the output gets nearer to the rail. This seems primarily due to frequency droop. Not surprisingly, the constant frequency design seems to do quite a bit better in this regard - about 4 to 5 times better (so maybe the UcD modulation scheme actually is less than optimum after all).
Or maybe I've made a mistake somewhere (I'll try to post the details of the analysis this weekend).Regards -- analogspiceman
Producing the attached output FFT takes about 5 minutes on my wife's Pentium M 1.7 laptop (my old Pentium II 266 can't handle it).
Here is a portion of the SPICE log file with the .four (DFT) data:
.step dc=30
DC component:29.2201
Total Harmonic Distortion: 0.009091%
.step dc=40
DC component:38.9236
Total Harmonic Distortion: 0.072294%
.step dc=45
DC component:43.7104
Total Harmonic Distortion: 0.220647%
.step dc=48
DC component:46.5436
Total Harmonic Distortion: 1.416930%
Total elapsed time: 252.743 seconds.
- - - - Here is a related post from the LTspice Yahoo group - - - -
Hello Luc,
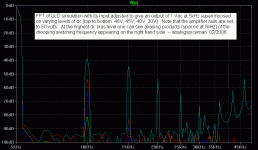
When running THD measurements in the lab on switching amps, a low pass filter is always required to lower the in-band (audio) noise floor. Too bad I didn't think to include one in my simulation, because it seems to help there as well. Thanks for the good idea.
With a four pole 50kHz low pass filter in place, I get about 90dB to 100dB of dynamic range in the FFT (a 30dB to 40dB improvement under certain conditions). It improves the resolution of the DFT as well. And you are right, the standard 16k (or even an 8k) FFT works as well as the larger FFTs for my class-d simulation.
It seems that the most important factors are: 1) pinning down the switching timing by specifying a very tight (0.1ns) triptdt parameter (my output stage is an a-device); 2) using at least 16 cycles of the test (base) frequency to get sufficient low end resolution and noise averaging in the FFT; and 3) low pass filtering the output signal that goes to the FFT (thanks again).
Items 1) and 2) above force the simulation to generate more than enough samples for the FFT, so it seems that specifying a maximum step size is not required. Also, as Gerd noted, neither the alternate solver nor reltol seem to matter much.
Look for ClassD_UcD180_simple_fft.asc here in the Temp folder.
Regards -- analogspiceman
Attachments
Hi analogspiceman,
thanks for all the hard work. I have currently too little time to perform simulations myself, so I can not post anything meaningful, but I read the thread with great interest.
I would just like to point to a topic that might have been overlooked, and that is PSRR of various modulation schemes. From my past simulations it seems that hysteretic modulator has very high PSRR which gets worse by synchronising to an external clock. IIRC, constant frequency hysteretic modulator from the patent I posted also had worse PSRR than bare hysteretic one. When simulating UcD, it would be fair to include addition to the circuit revealed by Bruno here.
Best regards,
Jaka Racman
thanks for all the hard work. I have currently too little time to perform simulations myself, so I can not post anything meaningful, but I read the thread with great interest.
I would just like to point to a topic that might have been overlooked, and that is PSRR of various modulation schemes. From my past simulations it seems that hysteretic modulator has very high PSRR which gets worse by synchronising to an external clock. IIRC, constant frequency hysteretic modulator from the patent I posted also had worse PSRR than bare hysteretic one. When simulating UcD, it would be fair to include addition to the circuit revealed by Bruno here.
Best regards,
Jaka Racman
Hi Jaka,
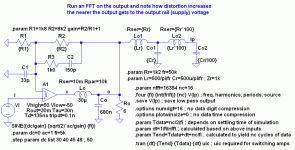
I followed the link but must be missing something because I don't understand why the UcD180 topology wouldn't naturally reject power supply noise. In the interest of speed and accuracy, my FFT simulation doesn't allow for dynamic variations in the power supplies, but it wouldn't be difficult to add it in (just have the comparator drive a pair of voltage controlled switches).
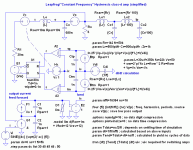
By the way, here's a gif of the simplified UcD schematic that was used to generate the FFT. - a.s.
Attachments
Hi,
I think it's because it's proportional to the feedback if you take no other measures. In the single ended version it was done with a simple divider from rail to rail tied to the inverting input with the feedback.
Regards,
Chris
I think it's because it's proportional to the feedback if you take no other measures. In the single ended version it was done with a simple divider from rail to rail tied to the inverting input with the feedback.
Regards,
Chris
power supply rejection
The reason UcD doesn't naturally reject ps noise is kind of complicated; it does feed back power supply induced errors so they get suppressed by the NFB. BUT the open loop gain is proportional to the power supply voltage.
So if the voltage dips, the loop dynamics change, the loop bandwidth is decreased, and the amount of NFB available for rejecting the dip is decreased, and vice versa for voltage increases.
The issue isn't the lack of rejection but the way the power supply voltage modulates the feedback characteristcs, so a UcD is essentially a voltage controlled filter whose control voltage is the power supply.
With a hysterisis scheme you can have an analog block that makes the hysteresis level depend inversely on the power supply voltage, so tha t the loop dynamics remain constant regardless of ps voltage.
The reason UcD doesn't naturally reject ps noise is kind of complicated; it does feed back power supply induced errors so they get suppressed by the NFB. BUT the open loop gain is proportional to the power supply voltage.
So if the voltage dips, the loop dynamics change, the loop bandwidth is decreased, and the amount of NFB available for rejecting the dip is decreased, and vice versa for voltage increases.
The issue isn't the lack of rejection but the way the power supply voltage modulates the feedback characteristcs, so a UcD is essentially a voltage controlled filter whose control voltage is the power supply.
With a hysterisis scheme you can have an analog block that makes the hysteresis level depend inversely on the power supply voltage, so tha t the loop dynamics remain constant regardless of ps voltage.
Well, maybe I am mistaken, but if you write down the transfer function of the Ucd, you have:
The comparator. This is an adder. It's gain is one, and it adds quantization noise.
The output stage: It's gain is the power supply voltage.
The output filter: a 2 pole frequency dependent transfer function.
The feedback filter: another frequency dependent TF.
The open loop gain is the product of those.
What did I miss?
The comparator. This is an adder. It's gain is one, and it adds quantization noise.
The output stage: It's gain is the power supply voltage.
The output filter: a 2 pole frequency dependent transfer function.
The feedback filter: another frequency dependent TF.
The open loop gain is the product of those.
What did I miss?
The combined gain of comparator and output stage is the ratio of supply voltage and "carrier" (at the input of the comparator) slew-rate. Since the latter is proportional to its amplitude (at a given frequency) which is by itself also proportional to the psu voltage the psu related gain-change is compensated for.
Regards
Charles
mirlo said:
An ideal comparator has infinite gain, but for the UcD it is probably best to think of the comparator/power stage as a single block with some finite delay and gain that is saturation limited to yield precisely unity loop gain at the frequency of oscillation.
The gain through the comparator/power stage is the ratio of the fundamental Fourier component of the switching frequency of the square wave output to that of the quasi sinewave input. It is auto adjusting.
- a.s.Lest this seem more confusing than it is, 😕 the above quotes are referring to related, but different gains. Charles was referring to the audio frequency transfer function (whose gain depends on slope of the carrier present at the comparator's input) and I was referring to gain at the switching frequency (where loop gain must always be unity).
Regards -- analogspiceman
analogspiceman said:
...The UcD seems to suffer increasing distortion, including nasty even harmonics, as the dc level of the output gets nearer to the rail. This seems primarily due to frequency droop. Not surprisingly, the constant frequency design seems to do quite a bit better in this regard - about 4 to 5 times better (so maybe the UcD modulation scheme actually is less than optimum after all).
Regards -- analogspiceman
Your work here is great.
What do you mean by "nasy even harmonics".
When I'm looking at amp distoriton, even's up to the forth, and maybe 6th can be ignored.
Were they monotonic, or was it a picket fence. Of coarse, this will all be obvious when you post, so I can wait. 🙂
It would be interesting to see a bridged UcD, one comparator, bridged fets. Bridge designs cancel even's I believe.
On your comment about the distortion being mostly due to the frequency shift, that's interesting. I've been simulating differnt modulators with complex poles and zeros to make the loop less insensitive to this. I did this awhile back, but thought maybe this wouldn't help since lower frequency in my experience ment less distortion becuase of less error pulses.... but the UcD driver topology seems to minimize this affect, so maybe it is an issue.
Oh, and about not reading the thread very well. Your correct on this, but what I I recall on the PC supply topology isn't was it used a sense resistor, and it was multiphase. It wasn't similar on many counts to the paper that started the thread. It was a National design for IMVP, but very similar to Sipex, or Semtech, can't remember which on. None are avialable to the non-intel client, but NSC got out of this, so maybe I can get a schematic.
Thanks
Mike
Attached to this post should be a gif of the LTspice schematic that generated the above FFT data. The design is highly idealized to capture the maximum potential of the topology and to increase simulation speed. In many places current sources paralleled with 1 ohm and 1nF have been used to enhance convergence performance of the spice engine (the 1 ohm makes the current sources functionally equivalent to voltage sources). – a.s.
Attachments
analogspiceman said:
An ideal comparator has infinite gain, but for the UcD it is probably best to think of the comparator/power stage as a single block with some finite delay and gain that is saturation limited to yield precisely unity loop gain at the frequency of oscillation.
The gain through the comparator/power stage is the ratio of the fundamental Fourier component of the switching frequency of the square wave output to that of the quasi sinewave input. It is auto adjusting.
OK ... this makes sense. My mistake was to think of the comparator as if it were in a sampled data system. If you were to put a sampler in front of the comparator, then the power supply voltage would cause loop gain variations.
- Status
- Not open for further replies.