completely useless for the general market. However, as an extreme DIY effort it interests me a great deal.
While the DIYers may reflect the general market in many ways, the glory of DIY, is that SOME of us can make what WE want. We just need some help sometimes, and I appreciate Earl giving out some help here.
O.T.
I would not recommend to sign in for any of googles webservices --> http://en.wikipedia.org/wiki/Gmail#Privacy.
Patrick Bateman said:It's single sign on, so if you use any of Google's products, using Google docs doesn't require an additional login. Personally I couldn't live without gmail; it's like a giant filing cabinet with the best search functionality I've ever seen. Another nice thing about Google docs is that it's cross-platform. This is nice since I use a Macbook, an OpenSolaris box and a Windows laptop.
I would not recommend to sign in for any of googles webservices --> http://en.wikipedia.org/wiki/Gmail#Privacy.
Variac said:
While the DIYers may reflect the general market in many ways, the glory of DIY, is that SOME of us can make what WE want. We just need some help sometimes, and I appreciate Earl giving out some help here.
 Amen to that!
Amen to that! 
I hope that we can get a really good calculator posted so that some wacko-big 'guides will be made!
Earl, a few posts up you wrote:
"Narrower angles improve loading at LF and reduce the HOM..."
I would have thought that a wider angle reduces HOM. Looking at the extreme cases, an ultra-narrow angle being a deep slot and a super-wide angle being the surface of a sphere, seems to me the trend is decreasing internal reflections as the angle widens.
What am I missing?
Thanks,
Duke
"Narrower angles improve loading at LF and reduce the HOM..."
I would have thought that a wider angle reduces HOM. Looking at the extreme cases, an ultra-narrow angle being a deep slot and a super-wide angle being the surface of a sphere, seems to me the trend is decreasing internal reflections as the angle widens.
What am I missing?
Thanks,
Duke
audiokinesis said:Earl, a few posts up you wrote:
"Narrower angles improve loading at LF and reduce the HOM..."
I would have thought that a wider angle reduces HOM. Looking at the extreme cases, an ultra-narrow angle being a deep slot and a super-wide angle being the surface of a sphere, seems to me the trend is decreasing internal reflections as the angle widens.
What am I missing?
Thanks,
Duke
I might have stated this in a confusing manner. Its not that the lower angle reduces the HOM, it moves them higher in frequency, which is better because HOM are like modes in a room. They start out widely spaced and then get denser and denser as the frequency goes up. Thus the density of them will be lower for a given frequency band as the angle narrows.
Your limiting examples are not very enlightening because of the situations. A narow tube - like a plane wave tube, will have the lowest density of HOM of any shape, thats why plane wave tubes are used for testing compression drivers. The modes tend to be pretty high in frequency.
And the spherical shape is also misleading because the density of HOM gets so high that its basically a continuum. In the continuum case there is virtually no delay in the HOM and as the angle widens the delay of the HOM gets smaller.
While the tube has the fewest HOM what it has are the most delayed and they would tend to have the greatest gain. A coincidence effect is at work here. My paper on Waveguide Theory Revisted clearly shows this effect. The gain rises with narrow angles, its reactive component increases and hence its group delay will increase - all subjectively bad things since audibility depends on level and delay. One aspect gets greater (level and group delay) while the other gets smaller (density).
Now is there a sweat spot? Thats a very good question. I would guess that the answer is also quite complex and it would take some serious investigations to sort it out. Based on the physics I would also guess that 45° is either the best or the worst - the min or the max. Judging by the sound quality of the waveguides that I have heard, I would guess its the best compromise.
A very interesting question - one that I will have to think about. Maybe in addition to the OS being the optimal shape, 45° is the optimal angle. This later aspect would have been complete luck on my part as I had never thought about this before.
Thank you, Earl!
Wow. Instead of stopping after you showed that my understanding of HOM generation as totally bass-ackwards, you derived the question that I SHOULD have asked and answered it.
And then you asked the implied question that I hadn't even thought of - namely, "what's the sweet spot?"
Based on my listening as well, I think that a 45 degree angle (90 degrees total included angle) is sure doing something right. And, it's practical to match it up with a woofer in the crossover region.
This is unrelated to HOM generation, but related to optimum radiation pattern angle. Roger West of SoundLab told me that many years ago he experimented with numerous different radiation pattern angles, from a flat panel all the way out to a 180 degree arc, in roughly 12 degree increments. His listeners concluded that approximately 90 degrees (same as the Summa) sounded the most natural. He used a large screen so that his listening panel couldn't see what they were listening to. This wasn't a peer-reviewed, controlled test (the listeners were probably well acquainted with what he was working on), but the intent was to find what worked best, not to justify what he was already doing, as he hadn't "done it" yet.
Okay if delay is one of the factors that drives audibility of HOM, does that imply that a smaller horn or waveguide is less likely to have audible HOM than a larger one, assuming they have the same shape? This assumes no foam insert; obviously the larger waveguide would have a larger foam insert.
Duke
Wow. Instead of stopping after you showed that my understanding of HOM generation as totally bass-ackwards, you derived the question that I SHOULD have asked and answered it.
And then you asked the implied question that I hadn't even thought of - namely, "what's the sweet spot?"
Based on my listening as well, I think that a 45 degree angle (90 degrees total included angle) is sure doing something right. And, it's practical to match it up with a woofer in the crossover region.
This is unrelated to HOM generation, but related to optimum radiation pattern angle. Roger West of SoundLab told me that many years ago he experimented with numerous different radiation pattern angles, from a flat panel all the way out to a 180 degree arc, in roughly 12 degree increments. His listeners concluded that approximately 90 degrees (same as the Summa) sounded the most natural. He used a large screen so that his listening panel couldn't see what they were listening to. This wasn't a peer-reviewed, controlled test (the listeners were probably well acquainted with what he was working on), but the intent was to find what worked best, not to justify what he was already doing, as he hadn't "done it" yet.
Okay if delay is one of the factors that drives audibility of HOM, does that imply that a smaller horn or waveguide is less likely to have audible HOM than a larger one, assuming they have the same shape? This assumes no foam insert; obviously the larger waveguide would have a larger foam insert.
Duke
audiokinesis said:
Okay if delay is one of the factors that drives audibility of HOM, does that imply that a smaller horn or waveguide is less likely to have audible HOM than a larger one, assuming they have the same shape? This assumes no foam insert; obviously the larger waveguide would have a larger foam insert.
Duke
I'm not sure on that one, but I believe that most of the delay would happen at the throat, but maybe the longer path length would also be a factor, making the delay longer for the longer waveguide. Thats not an easy question to answer.
A couple of questions.
Shouldn't a smaller waveguide move HOMs up in frequency? A larger room has lower axial modes, etc.
If I narrowed a horn\waveguide wouldn't I promote a lower frequency 1,0,0 and 1,1,0 modes over a 1,1,1 for instance?
Couldn't we look at unsmoothed frequency response to see which waveguide angle is better in dealing with these modes?
Shouldn't a smaller waveguide move HOMs up in frequency? A larger room has lower axial modes, etc.
If I narrowed a horn\waveguide wouldn't I promote a lower frequency 1,0,0 and 1,1,0 modes over a 1,1,1 for instance?
Couldn't we look at unsmoothed frequency response to see which waveguide angle is better in dealing with these modes?
mbutzkies said:A couple of questions.
Shouldn't a smaller waveguide move HOMs up in frequency? A larger room has lower axial modes, etc.
It does, but "small" means in cross section not in length. Don't mix the horns cross section with its lebgth because these are entirely different parameters that are for all practicle purposes uncoupled.
Variac said:I hope that we can get a really good calculator posted so that some wacko-big 'guides will be made!
Hi Variac,
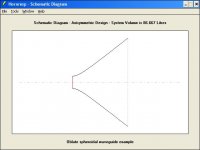
The Schematic Diagram Export tool in Hornresp can be used to obtain OS waveguide construction dimensions. The only constraint is that the throat entry angle is fixed at zero degrees.
Kind regards,
David
Attachments
G'day salas
Not sure how they sound but they are about the most beautiful horn speakers I've ever seen! Shame about the horn profile, it's an expo: http://www.google.com/patents?id=ZjUDAAAAEBAJ&dq=Zingali
Shame about the horn profile, it's an expo: http://www.google.com/patents?id=ZjUDAAAAEBAJ&dq=Zingali
Earl there might be some packaging ideas in there for you. They wouldn't be cheap to manufacture, but people who audition speakers with their eyes (The average high end audiophile) would be falling over themselves to have a listen. You shouldn't have to cut too many corners acoustically.
Thanks for the eye candy salas.
William Cowan
Not sure how they sound but they are about the most beautiful horn speakers I've ever seen!
 Shame about the horn profile, it's an expo: http://www.google.com/patents?id=ZjUDAAAAEBAJ&dq=Zingali
Shame about the horn profile, it's an expo: http://www.google.com/patents?id=ZjUDAAAAEBAJ&dq=ZingaliEarl there might be some packaging ideas in there for you. They wouldn't be cheap to manufacture, but people who audition speakers with their eyes (The average high end audiophile) would be falling over themselves to have a listen. You shouldn't have to cut too many corners acoustically.
Thanks for the eye candy salas.
William Cowan
Hello Cowan
Nice link, Earl will have all he needs so to comment.
Checked your site, wow! You certainly love BIG speakers.
Nice link, Earl will have all he needs so to comment.
Checked your site, wow! You certainly love BIG speakers.
Waveguide worksheet
alas, this pattern is also locked @ 90 degree entry angle
Josh's waveguide worksheet
alas, this pattern is also locked @ 90 degree entry angle
Josh's waveguide worksheet
salas said:Hello Earl
Can you comment on this ? Technical principles of its profile, claims in text. Its been around rather a lot in high$ home systems. It used Ciare woofer and B&C compression driver once I repaired a 15 inch one.
I've heard them and they are actually quite decent. But you better make A LOT of money to be in that ball game. They are very very expensive. I can't understand how he got the patent claim that he did - it seems so obvious to me and I'm sure that I could find prior art.
Yechnically, very wide waveguides like this are not such a good idea. But the low diffraction - not discontinuities - is a positive.
gedlee said:Yechnically, very wide waveguides like this are not such a good idea. But the low diffraction - not discontinuities - is a positive.
Why? Can you elaborate? Is it being shallow a rather bad idea too?
salas said:
Why? Can you elaborate? Is it being shallow a rather bad idea too?
Look up to the top of this page and the discussion with Audiokinesis and you will find your answer.
- Home
- Loudspeakers
- Multi-Way
- Geddes on Waveguides