I can't recall addressing this point and I am not sure that I understand it. Most often I just glide past a comment that I simply don't understand. (I mean these are forum posts - who can afford the time to be completely thorough?) All too often I assume that I did understand only to upset someone when in fact I didn't understand at all. So I stick to commenting only when I am pretty sure that I follow the logic.
I have now 😉
This time I watched each sub for how it affected excess GD. The process was very interesting particularly in disseminating the various first lower midrange reflections. Each making their own contribution at some frequency, adding subs can have the effect of improving the response whilst blowing out the GD. Cancelling out reflections can deepen a null and yet still improve the group delay.
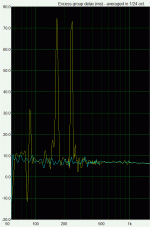
I have a screenshot of excess GD below showing where I was when I tried another sub setup routine a few weeks ago (which I didn't like the result of), and what I came up with today. I avoided any sub making the GD worse on its own. Whether this is necessary, I could only guess.
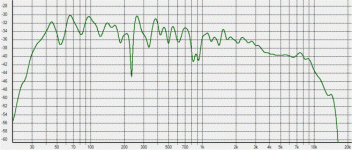
The response wasn't to good but I felt I had reached a point with the GD considered. So I cursorily EQed (shown in Holm), and listened.
So how did it sound? (Well, I think you should find out for yourself.) I thought I could produce a kick drum well. Hmmm, kick drum stood in the way of nothing and nothing stood in the way of a kick drum. Even when outside of the listening triangle. But this was more, and this lower midrange work even affected sibilants, cymbals etc.
I was listening to headphones last night and feeling disappointed that they had something I couldn't seem to put into data. I had stumbled across it before, I assumed it had something to do with the point source, or something to do with the reflections. Stupid, foreign built, didn't even cost $100, I was thinking to myself in my dissatisfied state.
The response of todays work isn't even flat, it isn't even impressive and yet music just seems to flow out of it...and louder
Attachments
@ Simon, by the way, I left the 200Hz and 900Hz issues alone as I felt they were borderline on flipping the GD. I already feel that was a good idea. More below.
I noticed that I could listen at much higher levels. Loud passages have the same clarity as much more quiet ones. I've always had this but never better than this. Worse recordings sound even worse at lower levels than before, but maybe this is just due to my adjustment to the better sound.
This makes me think of your diffraction papers, naturally. In each case there are multiple, related but time smeared sources.
Now, back to what I was talking about yesterday, notwithstanding what I've learned today. I was suggesting you can't correct a time shifted reflection/diffraction component even at one point in space.
Firstly assume two sources, identical and coincident. The second source is producing sound at the same time which is 140 degrees out of phase with the first. They sum destructively to -3dB. The problem is solved with EQ and the level is 0dB.
Now, move the second source back along the listening axis by one wavelength. Simultaneously apply two cycles at that wavelength to both drivers. The wanted result is two cycles at 0dB, but the received signal will actually comprise three cycles.
The first will be from the closer source at 0dB plus EQ equals +3dB. The second cycle will be one cycle from each driver summing to -3dB and EQed back to 0dB, then the farthest driver will finish with a cycle at +3dB.
The EQ would be correct if the signal were steady state, but becomes inaccurate the shorter the applied signal.
Thanks for your honesty. Before I rephrase it, I want to tell you my thoughts on my GD experiment.
I noticed that I could listen at much higher levels. Loud passages have the same clarity as much more quiet ones. I've always had this but never better than this. Worse recordings sound even worse at lower levels than before, but maybe this is just due to my adjustment to the better sound.
This makes me think of your diffraction papers, naturally. In each case there are multiple, related but time smeared sources.
Now, back to what I was talking about yesterday, notwithstanding what I've learned today. I was suggesting you can't correct a time shifted reflection/diffraction component even at one point in space.
Firstly assume two sources, identical and coincident. The second source is producing sound at the same time which is 140 degrees out of phase with the first. They sum destructively to -3dB. The problem is solved with EQ and the level is 0dB.
Now, move the second source back along the listening axis by one wavelength. Simultaneously apply two cycles at that wavelength to both drivers. The wanted result is two cycles at 0dB, but the received signal will actually comprise three cycles.
The first will be from the closer source at 0dB plus EQ equals +3dB. The second cycle will be one cycle from each driver summing to -3dB and EQed back to 0dB, then the farthest driver will finish with a cycle at +3dB.
The EQ would be correct if the signal were steady state, but becomes inaccurate the shorter the applied signal.
Your subs are going up into the lower midrange ? What frequency are they low passed ?
Not sure what you mean by cancelling out reflections, in this context. The nulls are generally caused by boundary reflections, so removing the reflections (not sure how you would do that physically) would reduce the null.
Ok so I'm assuming that in the first image the setup that you previously didn't like the sound of is the overlay in yellow with the large spikes in excess group delay, and the cyan response with quite a flat excess group delay is what you've achieved with your most recent reconfiguration ?
By the way I'm not sure what the significance of the negative going spike in your excess group delay is, in theory (?) excess group delay should always be positive relative to the overall baseline, since its a delay, so there could be a measurement error involved there, perhaps related to windowing of the impulse. All my excess group delay measurements have positive going spikes with a flat baseline except below about 30Hz which is probably due to insufficient FFT sample length to obtain high resolution at very low frequencies. Selecting a longer FFT length might help you there.
So let me see if I understand your comments, what you're basically saying is that you prefer the sound of the bass response which doesn't have any large spikes in excess group delay, even though the amplitude response is not quite as flat as other configurations ?
Again, not sure how to interpet that, except that you "like" the sound 😀 Can you try to describe the results a bit more ? Particularly the bass response.
Last edited:
I must be having one of those days 🙄 🙂
The new sub arrangement did help with the 240Hz reflection. The subs are crossed lower than that but still having an effect. you can see in the Holm plot that I didn't force the issue.
It seems that there are so many sources for these reflections (if you count each nearby wall, etc. etc), and modes, that if you try to target one particular frequency (for example) the end result can be a little hard to predict without trial and error. Not that it's an issue, just interesting.
I'm not certain about the negative going spike. I did truncate at 50Hz because I have mains issues with this sound card. Most of the excess GD seems to be at 7ms. I thought this odd so I plotted the woofer and tweeter individually and found the result to be different for the woofer than the woofer showed when plotting the whole system. From this I made some assumptions and stopped worrying about it.
I wasn't using windowing. My direct sound is somewhat dominant. The plot is low on resolution so as to show the GD spikes from my previous arrangement.
As far as preferring no GD spikes over a flat response, this is somewhat true. I've obsessed over a flat response in the past, and maybe it's essential at the other end of the spectrum. I could hear the unevenness of the response but it didn't seem to matter much. OK, it wasn't a good thing but it was educational to see how much it actually mattered today. I've produced bad sounding flat responses where the flat response itself was a good thing, but it wasn't enough to save the sound.
I can try to describe the subjective qualities. Lucid comes to mind. Smoothly flowing.
There wasn't that feeling of something being in the way. I guess to describe that, it's like standing partly behind something while listening, and when you listen it makes you feel like you need to focus like when you chat with someone in a room with extraneous noise.
Loud passages come through the same as quiet ones at even higher volumes than before, in fact I haven't found the limit just yet. Listening today, when a passage with slam came along I wished I'd thought to begin the song at a higher level. It's how a system of this excursion capability should sound.
It also feels like all the music is coming from the same point (more or less), just like headphones. I'm of the mind that the GD sounds like extra sources confusing the sound, and challenging for us to pull it apart in our minds as we listen. So the result is both more relaxed as well as being more detailed.
The new sub arrangement did help with the 240Hz reflection. The subs are crossed lower than that but still having an effect. you can see in the Holm plot that I didn't force the issue.
It seems that there are so many sources for these reflections (if you count each nearby wall, etc. etc), and modes, that if you try to target one particular frequency (for example) the end result can be a little hard to predict without trial and error. Not that it's an issue, just interesting.
I'm not certain about the negative going spike. I did truncate at 50Hz because I have mains issues with this sound card. Most of the excess GD seems to be at 7ms. I thought this odd so I plotted the woofer and tweeter individually and found the result to be different for the woofer than the woofer showed when plotting the whole system. From this I made some assumptions and stopped worrying about it.
I wasn't using windowing. My direct sound is somewhat dominant. The plot is low on resolution so as to show the GD spikes from my previous arrangement.
As far as preferring no GD spikes over a flat response, this is somewhat true. I've obsessed over a flat response in the past, and maybe it's essential at the other end of the spectrum. I could hear the unevenness of the response but it didn't seem to matter much. OK, it wasn't a good thing but it was educational to see how much it actually mattered today. I've produced bad sounding flat responses where the flat response itself was a good thing, but it wasn't enough to save the sound.
I can try to describe the subjective qualities. Lucid comes to mind. Smoothly flowing.
There wasn't that feeling of something being in the way. I guess to describe that, it's like standing partly behind something while listening, and when you listen it makes you feel like you need to focus like when you chat with someone in a room with extraneous noise.
Loud passages come through the same as quiet ones at even higher volumes than before, in fact I haven't found the limit just yet. Listening today, when a passage with slam came along I wished I'd thought to begin the song at a higher level. It's how a system of this excursion capability should sound.
It also feels like all the music is coming from the same point (more or less), just like headphones. I'm of the mind that the GD sounds like extra sources confusing the sound, and challenging for us to pull it apart in our minds as we listen. So the result is both more relaxed as well as being more detailed.
That's the big question - how to bring together FFT analysis and the way our hearing works. Our hearing is non-linear, knows things like forward and backward masking, it even memorizes sound.
My current approach to low frequency optimization with multiple subs is a) reduce point-to-point variance, then b) EQ everything flat. Don't forget to employ equal-loudness compensation because flat doesn't sound right.
Yes, well the more I think about it the more I just want to turn tail and design out anything that's not the direct sound. Only at least now I know that if it's MP I may not have to. I'm developing a soft spot for the professional speaker designer, knowing that many examples of their product may not be given the chance to see their full potential due to setup issues.
I've been doing some more listening and it's worth mentioning cymbal reproduction. The low hundreds of hertz are needed to get that tink and tizz (word used cautiously 😉 ) combination right. Maybe the only reason to mention this is that lower mid GD issues happen all to often, and I am fond of a cymbal's natural weight.
(OT, my 15" woofer does cymbals without giving away its size. I'll remember that next time I think about woofer speed.)
I used two subs this time. The locations for these woofers happened to be on the floor against the walls exactly opposite each other in the opposite side first reflection points. I think it says something about the problem of reflections. By the way I'll use the left over sub to flatten the bass later.
I also mentioned earlier that bad recordings sounded worse but I'm not so sure. Could've been a hasty judgement.
I've been doing some more listening and it's worth mentioning cymbal reproduction. The low hundreds of hertz are needed to get that tink and tizz (word used cautiously 😉 ) combination right. Maybe the only reason to mention this is that lower mid GD issues happen all to often, and I am fond of a cymbal's natural weight.
(OT, my 15" woofer does cymbals without giving away its size. I'll remember that next time I think about woofer speed.)
I used two subs this time. The locations for these woofers happened to be on the floor against the walls exactly opposite each other in the opposite side first reflection points. I think it says something about the problem of reflections. By the way I'll use the left over sub to flatten the bass later.
I also mentioned earlier that bad recordings sounded worse but I'm not so sure. Could've been a hasty judgement.
Our papers showed that GD has different audibility at different SPL levels - its audibility increases with SLP. So louder sounds better with lower GD systems. Its completly consistant with my research and practice.
What you say above is only true if the EQ is MP. If non-MP EQ is allowed then I can perfectly correct all situations at a single point. And they get much worse everywhere else. Think about it, it's no different than echo cancellation.
Except that this "anechoic" sound is not very pleasing. You need later reflections to add in spaciousness. Otherwise, I agree with you - that's what I do.
I actually find detail and imaging very pleasing. The question is how to add spaciousness without sacrificing the former - or, how to add spaciousness when it's appropriate. Not all content benefits from a concert hall type of sound.
I'm glad to be on track with group delay and it's antagonists. I'll stick with this in future.
This is me as well. I think I've always despised certain secondary sources. Most of my life naturally, I didn't even know what it was. Like most of us I assume, I've been fascinated with sound reproduction from a very early age and little has changed except my level of understanding.
However anechoic isn't perfect. I seem to like it more than many others but I agree with your summation of the problem.
My thoughts are to focus the direct sound past my listening position with as little interference as possible on the way, so that it will come back from the other end of the room with some reasonable delay under its belt.
With even narrower directivity I feel that a greater proportion of the total sound could be supported by the rear of the room. If the wider angles would only get themselves into trouble with early reflections anyway, it seems just like trimming the burnt edges from a piece of toast.
It's situations like this where I'd probably look up and think of DSP. However I'm holding out on getting into DSP in the interest of not leading myself into temptation. Maybe in five or ten years I'll see it from a different angle 😉
This is me as well. I think I've always despised certain secondary sources. Most of my life naturally, I didn't even know what it was. Like most of us I assume, I've been fascinated with sound reproduction from a very early age and little has changed except my level of understanding.
However anechoic isn't perfect. I seem to like it more than many others but I agree with your summation of the problem.
It may be the one extra element that I have in my equation, the fact that I listen in a multi-purpose room, that changes the rules. For example I have 12'^2 of fish tank that I built into one side wall before I realised how reflective that can be. I'm asked not to treat the ceiling, I don't want to overdo the floor, and my bass trapping is concentrated around (mainly behind and above) my mains. There is furniture.
My thoughts are to focus the direct sound past my listening position with as little interference as possible on the way, so that it will come back from the other end of the room with some reasonable delay under its belt.
With even narrower directivity I feel that a greater proportion of the total sound could be supported by the rear of the room. If the wider angles would only get themselves into trouble with early reflections anyway, it seems just like trimming the burnt edges from a piece of toast.
If you can control the room then this isn't so hard, but if the room is a given then your stuck - the age old story: "I want the very best, just don't change anything."
I find myself listening over headphones more and more. Maybe just a waypoint on the route to hearing aids?
Me too.
Unfortunately I think with 2 channel audio it's always going to be a compromise between the two that is set by the speakers and room.
To get good detail and imaging you want sound sources that are +/- 30 degrees from the centre line and a high direct to reflected ratio with fairly low levels of sidewall reflection, (directional speakers and/or absorptive sidewalls) on the other hand to get spaciousness you need significant signal levels at +/- 60 degrees or so from the centre line.
In stereo we can get that +/- 60 degree stimulation from the sidewall reflections but as you point out its not appropriate for all types of material (or even all instruments within a given recording) and its essentially "fake" information as its really just a time delayed copy of the +/- 30 degree signal arriving from a wider angle. We get a sense of spaciousness, but it's an auditory illusion.
I think if we had a discrete 4 channel recording system with 2 (fairly directional) speakers at +/- 30 degrees (for imaging and detail) and another two speakers at +/- 60 degrees, (for spaciousness) along with a fair amount of damping on the sidewalls it would be possible to have pin point imaging and spaciousness at the same time within a given recording, but of course that would require appropriately mastered material...
Any attempt to up-mix 2 channel material to such a 4 channel system is likely to make the wrong choices just like a physical wall reflection can't decide what's appropriate to add to spaciousness and whats not.
Last edited:
Fortunately many performances (almost everything that I lsiten to) were designed to be played back on two channels. They are not intended to "recreate" another space artificiially. This means that two channel IS NOT a compromise when the target of the performance is two channel.
Pen and ink drawings are not what a painting is, but they are NOT a compromise when the target medium was Pen and ink.
I think that a lot of people miss this point. It inevitable with the "I want to recreate a concert hall in my living room" crowd.
It may sound counter intuitive, but it is very simple.
An example, assume the system has flat frequency response for simplicity, so that its impulse is just a single time event. Assume the delayed impulse is half in amplitude of the original. What will the correcting filter's impulse response will look like? It will look like this, lets follow the event to correct:
First original impulse arrives, fine, than the echo in half amplitude, so we need in our correction filter an echo that is half in amplitude but negative of the echo. This cancels the echo. But this negative half in amplitude pulse in the correction filter then gets echoed from the filter being corrected, halved again in amplitude. So we need in our correction filter now 1/4 in amplitude and positive impulse at two echo time, to correct the echo of the 1/2 amplitude negative correction impulse. Then this 1/4 in amplitude correction impulse will echo as 1/8 amplitude, then we need a corrrection in our filter at 3 echo time 1/8 amplitude but negative pulse, and so on and on. The corrrection filter looks like this, an impulse of 1, then a negative impulse of 1/2, then a positive impulse of 1/4, then a negative impulse of 1/8, then a positive impulse of /16 and so on... The impulse of the correction filter is decreasing with time, so it is stable.
If you were to make the inverse of the FR of the echo system and took the inverse Fourier of it, the impulse would be just as I described.
BUT, if the echo had an amplitude greater than 1 (greater than the original impulse), then the correction filter's impulse will have impulses at each echo time interval whose amplitudes keep increasing and increasing. Which means the correction filter will be unstable, when the echo has amplitude greater than the original.
The above is for a baffle diffraction for a circular baffle, but for any baffle shape and result is that it is minimum phase.
The "minimum-phase" in linear system is defined as the linear system having a transfer function which has no zeros in s-plane that is to the right hand side of plane. In other words, no zero of the system has a real part that is positive. It it has a zero with a real part that is positive than it becomes non-minimum phase. Since all the speaker systems are passive, they are stable, so all their poles are on the left hand side of the s-plane, which means poles also have real parts that are not positive. If any pole has a real part that was positive it would give a part in the time domain (impulse response) that is like e to the power time with a coefficient of the power greater than 1. This of course means impulse response gets growing as time increases hence unstable.
If all zeros are on the left hand side of the s-plane, then the inverse of the function will have all its polese on the left hand side of the s-plane. So inverse becomes stable and realizable. That is why a minimum phase system can be corrected with a inverse function, and non-minimum can't be because its inverse function is an unstable one.
These are all from definition.
So to see if a linear systems transfer function is minimum phase or not, the most correct way is to look at this function's zeros. If all of them have real parts that are negative, then it is a minimum phase. Again this is by definition, it satisfies the definition (Again assuming we are dealing with stable system, i.e all poles are also on left handside of s-plane).
So, if you take a linear simple system that is made by the impulse plus its delayed echo and look at the real part of the zeros of this system, you will find that the sign of the real part of the zeros are completely dependent on the amplitude of the echo wrt to the original impulse. If the echo has less amplitude then the original the zeros have real parts that are negative, and vice versa.
So this simple echo system becomes minimum-phase if the echo does not have amplitude bigger than the original, which is most often the case but not always. In a circular baffle this is the case for diffraction. In other shapes it can be reduced to this case, and even including the higher order diffractions it can be reduced to this case.
In some cases echo can be greater than the originating signal, for instance in a small room where the walls are extremly reflective. The reflections from the walls if arrive at same time to the observation point can have a higher amplitude than the original sound, than it becomes non-minimum phase. In baffle diffraction this is not possible, because in simple terms, the most diffraction echo can have as magnitude is smaller than the original, regardless of the shape of the baffle.
Last edited:
I don't think spatial minimum phaseness is a correct terminology to use.
Because minimum phase is not defined for that purpose.
It is defined for a linear system looking at its transfer function's zeros. A 3-D system doesn't have just one transfer function. Even a single driver on an infinite baffle will have different frequency response amplitude curves at different angles, correcting for one angle will make it worse for other angles. I don't see this has any relation to whether or not a single transfer function has its zeros on left hand side of s-plane.
Because minimum phase is not defined for that purpose.
It is defined for a linear system looking at its transfer function's zeros. A 3-D system doesn't have just one transfer function. Even a single driver on an infinite baffle will have different frequency response amplitude curves at different angles, correcting for one angle will make it worse for other angles. I don't see this has any relation to whether or not a single transfer function has its zeros on left hand side of s-plane.
What you say above makes sense, and I have no argument with the possibility of correcting a delayed reflection (at one point in space) with a FIR type filter which is applying the inverse of the reflections impulse suitably time delayed and recursively to cancel it. (In fact I think I already mentioned this approach earlier in the thread)
However that's a FIR filter. What I still have difficulty with is seeing how an IIR filter that can be realised in the analog domain could achieve the same correction, at least without resorting to an actual analog delay line to provide the large amount of linear phase delay that would be needed.
If we don't have a source of pure delay, how can we cancel out the reflections impulse in the time domain ? Surely if we just correct for the frequency response and phase with an IIR filter we are only correcting the frequency response as measured integrated over a finite time window ?
Are you sure about that ? While most passive crossovers are minimum phase, as are most (but not all) individual drivers, there are drivers that are definitely not minimum phase, and there is also no reason why you couldn't use something like a lattice phase equaliser in a passive network if you really wanted to, leading to a non minimum phase transfer function in the network.
You seem to be trying to say that a passive network can't be non minimum phase just because its passive ?
That certainly explains the behaviour of rooms at low frequencies where parts of the response are minimum phase and parts aren't, and ties in nicely with the article markus76 linked to earlier...
What I explained is not a Finite IR filter, it is actually infinite IR, it keeps halving the echo impulses till infinity, they get smaller and smaller but don't end (untill they get down to noise level, but that is not the point).
Again you are mixing FIR and IIR. IIR and analog filters work on infinite time window, FIR on the other hand works on a finite time window that slides. That is why FIR is always stable, because its impulse is finite, it always dies at the end of its length.
BTW, what I wrote had nothing to do with digital or not. I went by definitions only on analog linear systems. The difficulty of implementing exacltly the inverse filter doesn't make it non-minimum phase, it makes it difficult to implement 🙂
I am sure, that is the definition of minimum phase. I didn't come up with it. It is all about having any zero to the right hand side of s-plane or not.
You can try to equalize some part and ignore some other that is fine. But if you wanted to equalize a non-minimum phase in all its frequencies, the inverse filter will be unstable.
As a side note, there are(is) digital time reversing manipulation technique(s) that approximately can correct non-minimum phase in FIR, but it can't correct all cases. Its filter time length has to be at least same as the system's impulse length that it reaches to noise floor of the environment.
No I didn't say that. A passive lattice is non minimum phase if I remember correctly. "Ladder networks" are always minimum phase from what I remember.
I haven't read the whole thread, I just saw my name and replied.
Last edited:
- Status
- Not open for further replies.