I have to agree with Syn08. I really don't know what you are trying to show here. As mentioned many times before, you argue over where we know there is an overlap in behaviour (so what?) and/or with sub-optimal circuits and the result is we just go around.
I will step out of this discussion for a while.
Scott, I'm not arguing for the general usefulness of such measurements, just that for a constant ib, partial ic w.r.t. vce seems pretty constant as the DC value of vce is varied.
Scott and Ian, I intend to measure ic/vce with constant ib on a number of 2N3904's I have. I'll repeat with constant vbe and with Ie set to 1mA. It'll be nice to check this against the two versions of models in LTSpice that Ian discussed. Any suggestions/comments regarding such a test?
As no one disputed your translation, I guess everyone agrees with.
So I have to congratulate you as you demonstrate the assertion from Forr :
A CFA is an Unbuffered VFA.
Doing the same test as with the BC550 in #2119, I got Ro=196K @ Ie=1mA for the 2N3904 with LTSpice.
Hans
Resolving the differences might be difficult. The point was when you force base current Vce modulation will change Vbe and forcing Vbe the Ib is what changes.
A lack of response never supports a conclusion of agreement Herve.
The Thevenin translation is of a basic form that doesn't yet include the significance of the internal Ro of the In- terminal, being in series with the translation. This Ro isn't a real Ro, rather a function of some equivalency of a transistor operating at some current, as I perceive being the object of discussions currently taking place.
The determination of a CFA being a CFA or VFA is considered, in my thinking, dependant upon the value of R Thevenin (Rf and Rg in parallel) in relation to the Ro as seen into the In- terminal. It is unclear if there exists any alignment with the results using Middlebrook, although it too is looking into the In- input.
So then, if I take the buffer off of a VFA I end up with a CFA?
That doesn't seem very useful in trying to decide whether a circuit is a VFA or a CFA; you just shifted the problem to the problem of defining 'what is a buffer' or 'what is a VFA' in this context.
'A VFA is a buffered CFA' is just circular.
Jan
Last edited:
Which was first stated in post #60 more than a year ago in this thread, albeit in the reverse notion of a VFA being a buffered CFA.
Happy New Year!
EDIT: What's a CFA then? To me, an OpAmp-type closed-loop circuit whose open-loop gain is *not* independent of the network impedance presented on the (-)-input pin, actually OLG scales well with network transconductunce over a reasonably wide range. This happens to lead to the first-order independance of BW vs gain with the standard Rf, Rg gain network, with Rg varied.
Last edited:
A french proverb says the contrary : "Qui ne dit mot consent."
What is Ro ? Zin- ?
I give back to you the definition which I completely agree.
Happy new year to every one !
My opinion is that we should distinguish between CFA and VFA (which I prefer to use to denote topologies), and current and voltage feedback (c.f and v.f.), which can be measured by MDIT.
In a CFA topology, input stage signal current flows through the feedback network (which in some cases can do double duty as a bias network.) In a VFA, this doesn't happen. Of course, composite designs with two different types of feedback can exist. If these come into wide use, it might make sense to assign a separate name to such.
It can be shown that at adequately high loop gains, if Rf || Rg > Z(in -), c.f. predominates. Otherwise, v.f. does. Of course, the application of MDIT has the final say.
I was curious about the internal behaviour when CFA's is in invertingn closed loop configuration, alos said "virtual ground". I have never seen this scheme used for CFA's but it seems to work as. intended with the inverting input being very close to the ground potential.
The first circuit has it gain set by the negative feedback divider Rfi/Rgi.
The second one is a transimpedance circuit, its output voltage being equal to the voltage across feedback resistor Rft due to current Igt.
Current Ie and voltage Vbe of input transistor T1 have very stable values for variations of Rg from 2 Ohm up to 20 kOhm.
The first circuit has it gain set by the negative feedback divider Rfi/Rgi.
The second one is a transimpedance circuit, its output voltage being equal to the voltage across feedback resistor Rft due to current Igt.
Current Ie and voltage Vbe of input transistor T1 have very stable values for variations of Rg from 2 Ohm up to 20 kOhm.
An externally hosted image should be here but it was not working when we last tested it.
An externally hosted image should be here but it was not working when we last tested it.
Last edited:
Bingo!
Note: not any dependences of the OLG on the feedback network will provide the CFA small signal properties, it would be more correct to state that in a CFA the Loop Gain depends on the feedback resistor only (and not on the noise gain as in a VFA).
Last edited:
The smilies on this forum have been the same for donkeys' years and are rather a mixed bag with notable omissions. I just can't find the right one. Instead, here's something seasonal
It's appeared on every data sheet for years and I suggested a while ago it makes things clearer. Maybe you have missed some other things?
I've made lots of use of this with the AD844. Like with any honest CFA, current at -in = output current at Tz. So you can set voltage gain by the ratio of series R at -in to load R at Tz.
Jan
Jan
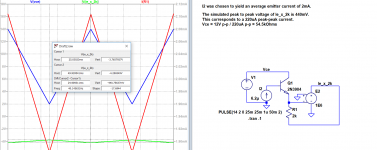
As threatened 🙂 I measured the Early resistance ro of a 2N3904 at Ie = 2mA on the bench and compared it to that predicted by an LTSpice sim. The results differed by a factor of 2.5 (134k measured vs. 54.5k simulated.)
I don't know the variations of ro from transistor to transistor, but this seems reasonably close. It would appear to be a confirmation of the sim I did showing the CFA gm and ro input transistor current contributions becoming almost equal at high at loop gains. I question whether it justifies disposing of the Gummel Poon models in favor of the VBIC versions, but I'd be interested in others' comments.
Attachments
VBIC update
The anomaly I found in the GP model was specifically the ratio of Ic6/Vbe. When the Tz termination resistance was varied in your test circuit (Post 1872 AD844) Current Feedback Amplifiers, not only a semantic problem? you found a massive unexpected drop from 38mS to 0.15mS!! when this should not change much at all.because you are only altering the termination resistance of the output of the current mirrors and there should be negligible change in the DC bias.
I don't see how just measuring the Early effect resistance 'ro' relates to this anomaly. I think you would need to make the circuit you simulated and bench test it to find the ratio of Ic/Vbe for Q6 with AC signals.
As I demonstrated with the VBIC model in your circuit the ratio of Ic to Vbe was quite close to the expected constant gm value of 30-40mA/V at 1mA. and that over the wide range of Tz loading resistances.
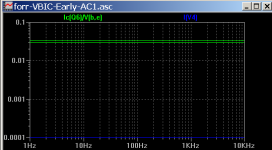
I have since found the VBIC's small spread is mainly determined by the choice of parameter 'mc' which is MJC in the GP (base-collector capacitance exponent). The attached plot shows the two plots with mc=0.75 (earlier BC550C_V was 0.25). I don't understand the theoretical basis why this capacitance parameter affects the Ic/Vbe in this way - charge based models are still a mystery to me. Perhaps someone can explain why it is so from the physics?
I'm not saying we have to ditch the present GP model in LTspice etc. It's just we cannot use it to resolve the query that CPaul raised concerning the Early effect and the transconductance in the input stage of a CFA. With the VBIC model the gm transconductance of the input stage is seen to be controlling the current to the mirrors. The GP model fails to resolve your query. For most other simulations the GP model is very good.
Cheers,
Chris,
The anomaly I found in the GP model was specifically the ratio of Ic6/Vbe. When the Tz termination resistance was varied in your test circuit (Post 1872 AD844) Current Feedback Amplifiers, not only a semantic problem? you found a massive unexpected drop from 38mS to 0.15mS!! when this should not change much at all.because you are only altering the termination resistance of the output of the current mirrors and there should be negligible change in the DC bias.
I don't see how just measuring the Early effect resistance 'ro' relates to this anomaly. I think you would need to make the circuit you simulated and bench test it to find the ratio of Ic/Vbe for Q6 with AC signals.
As I demonstrated with the VBIC model in your circuit the ratio of Ic to Vbe was quite close to the expected constant gm value of 30-40mA/V at 1mA. and that over the wide range of Tz loading resistances.
I have since found the VBIC's small spread is mainly determined by the choice of parameter 'mc' which is MJC in the GP (base-collector capacitance exponent). The attached plot shows the two plots with mc=0.75 (earlier BC550C_V was 0.25). I don't understand the theoretical basis why this capacitance parameter affects the Ic/Vbe in this way - charge based models are still a mystery to me. Perhaps someone can explain why it is so from the physics?
I'm not saying we have to ditch the present GP model in LTspice etc. It's just we cannot use it to resolve the query that CPaul raised concerning the Early effect and the transconductance in the input stage of a CFA. With the VBIC model the gm transconductance of the input stage is seen to be controlling the current to the mirrors. The GP model fails to resolve your query. For most other simulations the GP model is very good.
Cheers,
