Dave, I suspect you've probably forgotten more than I will ever know about speaker design but this statement isn't quite inaccurate.
In only 1 case does halving a panel result in a doubling of the resonant frequency and that is when you half the surface area of a square panel. So 40" x 40" to 28.3" x 28.3" or 20" x 20" to 14.1" x 14.1" and so on and so forth. In these cases, the ratio of length to width remains the same (1:1) but the surface area is exactly halved which effectively means the mass of the panel is also halved. Exactly the same situation as when you double a panel's thickness while keeping the same dimensions and thereby double its mass and double its resonant frequency too.
In all other cases, one must take into account both the change in mass and the ratio of the different panels' length to width to determine the change in the resonant frequency (as long as one is dealing with the same material). That is simply the nature of the equation for the resonant frequency of fixed edge panels. (More details for the math inclined)
So in the case of square panels, if you actually half the dimensions instead of the surface area (so 12" x12" to 6" x 6", etc. etc.), the change in the resonant frequency is actually much greater than when you just halve the panel's surface area/mass - upwards of 3 to 4 times higher depending on the original size of the square or in other words, the change in mass. Theoretically anyways.
In the case of rectangular panels (or square panels divided into rectangular panels), the change to the resonant frequency is going to depend on the actual panel dimensions. So the degree of change in the resonant frequency of a 20" x 12" panel braced in the middle to two 10" x 12" panels, or a 12" x 12" panel split to 12" x 6" panels as examples will be different. Again, it will be based on what the actual changes are. Sometimes the change to the resonant frequency is less than doubled and sometimes it'll be a more.
Bracing will raise the panels' resonant frequency higher than doubling the thickness. A cuboid remains inherently the worst possible shape for a given volume as it has large panels, so consider a multi-sided shape comprised of smaller panels to start with, when bracing becomes far simpler, more effective, and eats up less internal volume. These enclosures brace every other side together along with the rear panel. The lowest resonant frequency is several octaves above the pass band. If you are tempted to add damping to a dedicated sub enclosure, be absolutely sure that you don't lower its fundamental resonance too much or it will do more harm than good. Generally, damping is a waste of time, money, effort, and volume in a properly designed dedicated sub enclosure. Subs need stiffness, mids need damping.
Last edited:
Anyone thought about panel excitation by the reactive forces in the driver chassis? To me these are far more problematic than the airborne sound transmission through the panels (yes, i know about mass law and coincidence effect, which are only partly of any use btw).
That is where almost all of the energy to excitr panel resonances comes from. Only in a woofer do we have the additional issue of ballooning.
dave
I should have said approximately. The smaller dimensions plays a more significant role i think than you have described. And if one follows the rule that the subpanels created by the brace have a higher aspect ratio then the panel being braced so one never runs into a bracing situation where the pnel still has the same aspect ratio\io never happens.
dave
Point is, I don’t think ‘ballooning‘ leads to much sound output. Unless resonances come into play.
Balloning is the primary resonance of (usually) an unv=brced box. It is the most intrusive “resonance" possible. Not just a single panel resonating but the whole box actingas a coherent radiator.
dave
dave
In all simplicity
Seems bracing according to the math is
More effective.
Speaker baffle is the hardest
To brace. Or would have least available area to tie in bracing.
Seems incredible common to have double layer baffle. Then well braced side and rear walls. And try to tie in the bracing as much as possible to the front/speaker baffle.
Obviously designs vary. But assume speaker baffle has least amount of bracing. And double wall is easy solution
Seems bracing according to the math is
More effective.
Speaker baffle is the hardest
To brace. Or would have least available area to tie in bracing.
Seems incredible common to have double layer baffle. Then well braced side and rear walls. And try to tie in the bracing as much as possible to the front/speaker baffle.
Obviously designs vary. But assume speaker baffle has least amount of bracing. And double wall is easy solution
Dave, I don't think you and I are really disagreeing over the importance of the panels' aspect ratio (or the ratio of its length to width in my words) in determining a panel's resonant frequency. Just for clarity's sake though, even saying splitting a panel in half will result in approximately a doubling in the resonant frequency isn't always accurate.
Here's another example using 3/4" Baltic Birch and the resonant frequency (Fr) equation I linked to above:
Fr for a 30"x12" panel = 359Hz
Fr for a 30"x6" panel = 1286Hz (halved length ways gives an increase by a factor of 3.58)
Fr for a 15"x12" panel = 507Hz (halved width ways gives an increase by a factor of 1.41)
So obviously, splitting it in half length ways is the way to go which I know is exactly what you have been saying for years, but in neither of the cases I just gave would I call the increase in the Fr to be close to approximately a factor of 2. A factor of 1.5 is sort of close but a factor of 3.5 isn't really even in the ballpark. And this is just one example. I've done the math. I've put the equation into a spread sheet and worked it out for all kinds of dimensions for both Baltic Birch and MDF so I know exactly what is going on in terms of the theoretical numbers. And among the things I learned is again, that the actual dimensions under consideration matter. Halving a panel may result in approximately an increase in Fr by a factor of 2 or not. It all depends.
Here's another example using 3/4" Baltic Birch and the resonant frequency (Fr) equation I linked to above:
Fr for a 30"x12" panel = 359Hz
Fr for a 30"x6" panel = 1286Hz (halved length ways gives an increase by a factor of 3.58)
Fr for a 15"x12" panel = 507Hz (halved width ways gives an increase by a factor of 1.41)
So obviously, splitting it in half length ways is the way to go which I know is exactly what you have been saying for years, but in neither of the cases I just gave would I call the increase in the Fr to be close to approximately a factor of 2. A factor of 1.5 is sort of close but a factor of 3.5 isn't really even in the ballpark. And this is just one example. I've done the math. I've put the equation into a spread sheet and worked it out for all kinds of dimensions for both Baltic Birch and MDF so I know exactly what is going on in terms of the theoretical numbers. And among the things I learned is again, that the actual dimensions under consideration matter. Halving a panel may result in approximately an increase in Fr by a factor of 2 or not. It all depends.
Certainly the detail is interesting. I probably covered the theory at Uni but haven’t paid much attention to the detail. It is nice to see from the figures you have shown, where i have gotten to with bracing is even better than i figured. You will note from the example above that all the subpanels have significantly high aspect ratios for the subpanels.
Thanx for the remedial physics lesson :^)
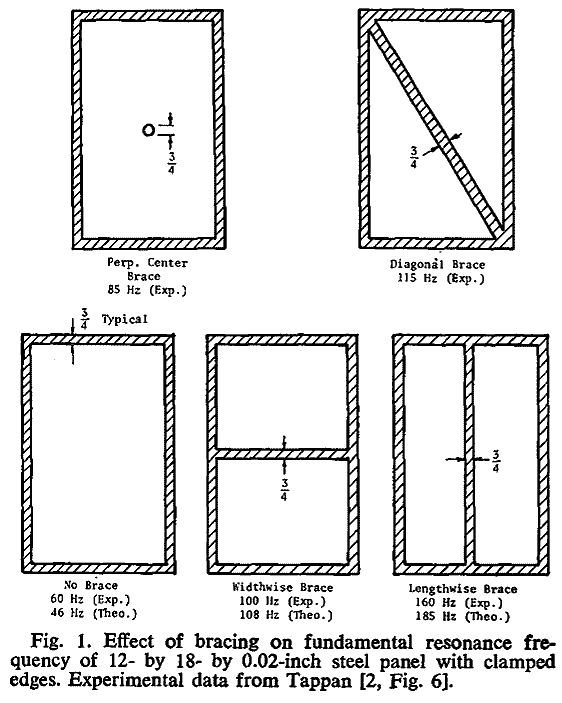
I have mostly just gone in the directions driven by Tappen’s early work.
dave
Thanx for the remedial physics lesson :^)
I have mostly just gone in the directions driven by Tappen’s early work.
dave
I just want to add a quick clarification to the discussion. I am sure that most people are aware (particularly Planet10 and jReave) that a real world box is more complicated than a single panel. The algorithms that calculate a resonance frequency of a panel usually assume the panel is either simply supported at two or four edges, or that it is in free space with no edge constraint. A real box has some amount of fixity on the edges which can impart a restraining end moment, so it is neither cantilevered nor simply supported, but something in between. There is also interaction between the 6 panels of a box. Bracing complicates it quite a bit more.
But this complexity does not change the meat of the discussion... Bracing makes the box stiffer, which drives up the resonance frequency and makes the resonance a higher Q. This makes the resonance less audible, and less likely to be energized.
j.
But this complexity does not change the meat of the discussion... Bracing makes the box stiffer, which drives up the resonance frequency and makes the resonance a higher Q. This makes the resonance less audible, and less likely to be energized.
j.
In appreciation for that idea, I'll add my 2c worth. How about pre-stressing the structure? A big, threaded rod from the panel center to the opposite and start cranking it down. Not to structure failure of course, but to some significant effect on the ballooning or panels otherwise flapping about.
If you could get an even grip on the driver basket, you could pull hard on it from the rear panel. Pushing on the magnet would be easier.
In a panel ply layup, it would be interesting to have a crosshatch of plastic shipping strap - but with, say 1000 lbs of tension on each. Allow the epoxy to dry, like an analogy to pre-stressed rebar reinforced concrete beam construction. What composite structure would be created for a cabinet panel then? I'd bet that would be a pretty stiff panel.
If you could get an even grip on the driver basket, you could pull hard on it from the rear panel. Pushing on the magnet would be easier.
In a panel ply layup, it would be interesting to have a crosshatch of plastic shipping strap - but with, say 1000 lbs of tension on each. Allow the epoxy to dry, like an analogy to pre-stressed rebar reinforced concrete beam construction. What composite structure would be created for a cabinet panel then? I'd bet that would be a pretty stiff panel.
You want a subwoofer?
Forget everything you think you know and everything they are telling you.
Think outside the box.
Think tubular... something like those pipes we had in college, just a little, ahem... bigger...
https://www.passdiy.com/project/speakers/the-legend-of-el-pipe-o
I think it’s unlikely a whole box would have one resonant frequency. And if it had one, it’s probably outside the passband of the subwoofer, given a reasonably solid build. So my point remains, do we have a problem, from an acoustical point of view?
Midrange enclosures of course are in another ballpark. But still we should regard the acoustic output from the enclosure, not the vibration itself. To give one clue: smaller is better.
[Edit]About the ballooning: 100dB SPL equals 2N per square meter. I’m too lazy to calculate the excursion under that load of a panel of -say- 0,4x0,6m which is clamped on all four sides, but it is -ehh- quite small.
Last edited:
I see that my conclusion from my last post was probably calculated with a modle wich was too simple, i just did the quick maths for a simple one and two span beam. So today i used a program for very simple 2D stress resultants calculations. A 3D calculation would of course be more accurate but i'd assume we would get similar results). I modeled a 500 x 500 mm wooden square ( about 19.5") of 18mm (~3/4") and 36 mm thickness. The Square has perfectly stiff edges, which actualy makes a big difference in deflection. I also ran the Program with pivoting joints and derived at similar numbers as in my first simple calculation with double wall thickness being 8 times and bracing being 30 times stiffer than the normal unbraced box (before i calculated 40 times). That deviation from 40 to 30 times is due to the elasticity of the brace itself which i didn't take into acount before.
I assumed 20 Pa of pressure inside the box. I don't know if thats realistic for, say a 15" woofer at full excursion or not but just for comparing the results it doesn't make a difference, the numbers would only get bigger or smaller linearily.
Anyways here are the deflection calculation results:
The units are in mm and the numbers in the brackets are (deflection in x direction, deflection in y direction, rotation)
18mm, stiff joints, no bracing: max deflection wmax = 0.175 mm
36 mm, stiff joints, no bracing: wmax = 0.0084 mm (20 times stiffer)
18 mm, single brace: wmax = 0.28 mm (1.6 times less stiff)
18 mm double bracing: wmax = 0.011 mm (16 times stiffer than 18mm no bracing)
That was quite surprising for me, that the stiff edges make such a big difference, so much that the double wall thickness becomes stiffer than double brace. Also i would stay away of just one single brace, even if thats way easier to build. As you can see the deflection on the "free"panel is larger than with the unbraced box.
With that in mind i would conlude: The stiffness of a box depends on the execution of the box edges as hifijim stated before. I would consider a well fitting and glued Box joint as a pritty stiff edge joint and a screwed or even nailed butt joint as quite an elastic edge. The actual deflection lays somewhere between these numbers, depending on the stiffnes of the edge, as every connection between two parts is a spring.
I hope that helps.
I assumed 20 Pa of pressure inside the box. I don't know if thats realistic for, say a 15" woofer at full excursion or not but just for comparing the results it doesn't make a difference, the numbers would only get bigger or smaller linearily.
Anyways here are the deflection calculation results:
The units are in mm and the numbers in the brackets are (deflection in x direction, deflection in y direction, rotation)
18mm, stiff joints, no bracing: max deflection wmax = 0.175 mm
36 mm, stiff joints, no bracing: wmax = 0.0084 mm (20 times stiffer)
18 mm, single brace: wmax = 0.28 mm (1.6 times less stiff)
18 mm double bracing: wmax = 0.011 mm (16 times stiffer than 18mm no bracing)
That was quite surprising for me, that the stiff edges make such a big difference, so much that the double wall thickness becomes stiffer than double brace. Also i would stay away of just one single brace, even if thats way easier to build. As you can see the deflection on the "free"panel is larger than with the unbraced box.
With that in mind i would conlude: The stiffness of a box depends on the execution of the box edges as hifijim stated before. I would consider a well fitting and glued Box joint as a pritty stiff edge joint and a screwed or even nailed butt joint as quite an elastic edge. The actual deflection lays somewhere between these numbers, depending on the stiffnes of the edge, as every connection between two parts is a spring.
I hope that helps.