Would the elimination of round-overs reduce the susceptibility to reflections from objects behind and around the horn?
I see that the roundover helps clean up the curve but is there a downside?
I see that the roundover helps clean up the curve but is there a downside?
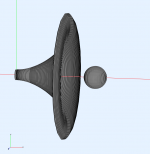
A problem that has always intrigued me is to put a sphere, on axis, at some distance out. I think that there might be a possibility of tuning the axial and off-axis responses separately with variations in the sphere's radius as well as the distance. Spheres have the least and smoothest diffraction of any shape.
While you are at it add multiple entry horn tap(s) to the simulation list please 🙂 Again, thank you very much, this is the coolest thing you are doing mabat!
What do you think about the Azura-horn AH-204 for 600 hz Xo ?
It's crazy expensive, but an aussie mate purchased it while not bought a driver for them yet ! Said to be JMLC profile, Does it look good or is it impossible to kno from the picture here (scroll a little) : Azurahorn -Le Cleac'h Acoustic Horns - Products !
you have to cut at the right length to have the hoped apex overture... then I assume you have to add a piece of some wood to tied the driver ?!!! Crazy no, at least for that price (well it's Australia where all is expensive though.
It's crazy expensive, but an aussie mate purchased it while not bought a driver for them yet ! Said to be JMLC profile, Does it look good or is it impossible to kno from the picture here (scroll a little) : Azurahorn -Le Cleac'h Acoustic Horns - Products !
you have to cut at the right length to have the hoped apex overture... then I assume you have to add a piece of some wood to tied the driver ?!!! Crazy no, at least for that price (well it's Australia where all is expensive though.
Last edited:
One (impractical) way to reduce / eliminate the influence of objects around the backside of the horn is to make the mouth much bigger than necessary for the frequency range used.
This could essentially be demonstrated in Akabak, e.g. by simulating an axisymmetrical waveguide with a mouth diameter of 1.50m between 600Hz-20kHz.
This could essentially be demonstrated in Akabak, e.g. by simulating an axisymmetrical waveguide with a mouth diameter of 1.50m between 600Hz-20kHz.
Last edited:
I've been paying attention to the developments by Meyer Sound. It seems like they really know what they're doing and based on my experience they produce very good sounding products. The X40 is a different approach to the two-way sound source, while their studio flag ship products have not gone to complete round over horn designs, it makes me wonder if there are downsides to that approach. Still two-ways but with an emphasis on flat phase response.
Take the blue horn system or Acheron - large wave guide but no round over horns.
Take the blue horn system or Acheron - large wave guide but no round over horns.
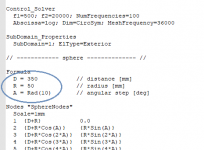
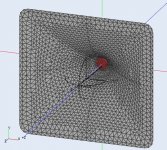
Really? Well that's a piece of cake in the CircSym mode in ABEC- if you have the possibility to run ABEC or AKABAK, attached is a complete project with a sphere placed on axis.
The distance and radius are parametrized in the script (solving.txt):
Attachments
Last edited:
That's why I said that there was a hope because the example I showed (in the CircSym mode) was obviously the worst case possible. And frankly, I expected bigger problems.
That's not the way to go, believe me. Eliminating the round-overs, either on the waveguide or on the baffle/enclosure, always leads to a worse performance, not better.
BTW, as for the sphere on axis - thinking about that, one can add such a sphere even now in Ath by using the source definition script (Chapter 7.5 of the User Guide). This way it's possible to define virtually any additional axisymmetric structrure to any Ath project, including all different kinds of phase plugs.
Last edited:
I've been playing around with some different versions based on the ideas mabat showed in post #3306
Acoustic Horn Design – The Easy Way (Ath4)
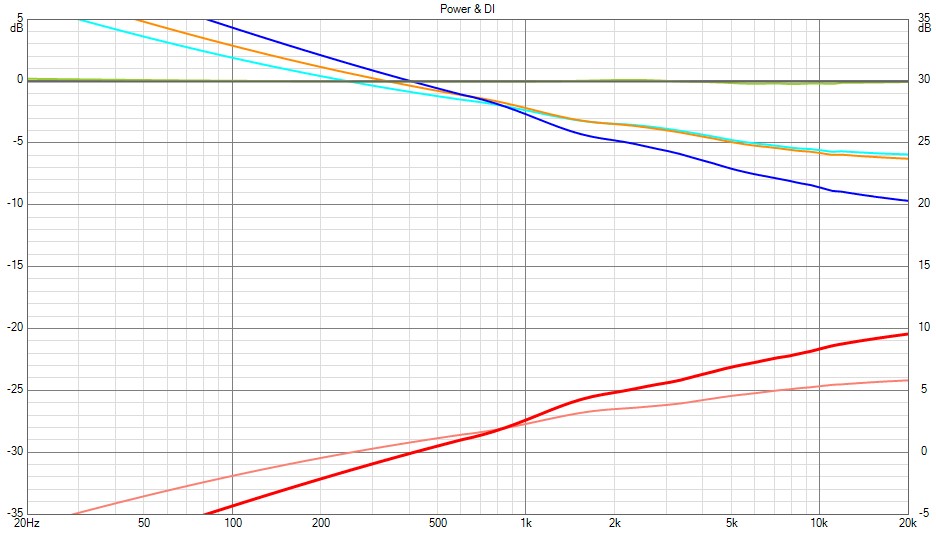
When I saw the two contours side by side it reminded me of the Yuichi / TAD horns where the Horizontal is conical or almost, and then the vertical has more flaring. I wanted to see what effect that had on the DI as the horizontal and vertical curves are very smooth.
This was designed to match with the Faital HF108 and be about the same size as a 12" driver.
DI
Mesh
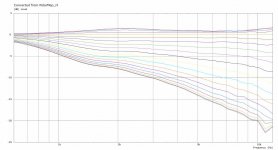
I think the contrast between the ERDI and the overall half space DI is interesting. Within the listening window everything is very flat and quite well controlled but the further off axis you go the steeper the curves fall off but still very smoothly.
Acoustic Horn Design – The Easy Way (Ath4)
When I saw the two contours side by side it reminded me of the Yuichi / TAD horns where the Horizontal is conical or almost, and then the vertical has more flaring. I wanted to see what effect that had on the DI as the horizontal and vertical curves are very smooth.
This was designed to match with the Faital HF108 and be about the same size as a 12" driver.
DI
Mesh
I think the contrast between the ERDI and the overall half space DI is interesting. Within the listening window everything is very flat and quite well controlled but the further off axis you go the steeper the curves fall off but still very smoothly.
Attachments
I made another bigger one to see if I could get the same sort of DI as I did on my best effort with a super shape. By making the vertical contour more similar to the horizontal the DI got flatter over a bigger range. There is a bit of an 8K wiggle in this one which makes the curves look not quite so nice but still promising. This one is a 15" size.
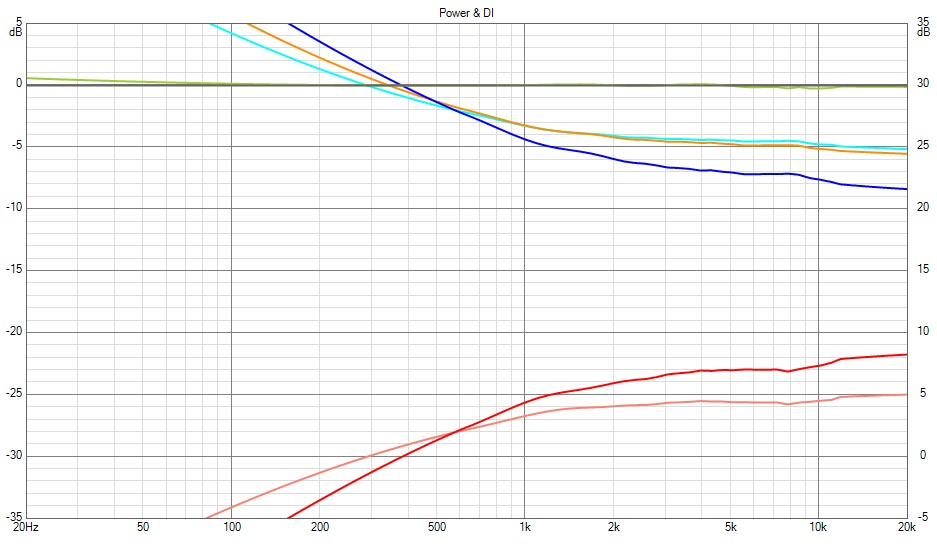
Attachments
I don't know how is that profile calculated as I've always considered that as beaming too much to be really useful. If someone provides me the coordinates, I can simulate it. I can't really judge without such data.
Last edited:
I think people are interested in it for horns (especially P.A.) to get high volume without a coax compression driver, and still get a point source to a low frequency. not many cheap compression drivers that get to 500 hz
My CNC is ready to make these for real (for my Axi2050s) - I've made similar before but with a profile I just guessed. Would you be happy to share the curve? I'm planning to make the first 100mm in one throat-piece and morph to solid wood petals for the rest. I'll share measurements.
Attachments
Some interesting quotes by le maître:
The nearest conventional (= old) profile to the Le Cléac'h profile is the Kugelwellen horn (here compared among with other profiles to the Tractrix and T = 1 Le Cléac'h horn).
Notice that the Kugelwellen follows the same logic as the Tractrix ("constant speed" translation of spherical cap wavefronts of a constant radius along the axis. The radius used for the Kugelwellen being 2 times the radius used for the Tractrix).
A main difference between the Tractrix and the Kugelwellen is that the Kugelwellen expansion is exponential all along but the expansion of the Tractrix (as I calculated it) departs from an exponential law near the mouth. If we recalculate the tractrix with a pure exponential expansion of spherical cap wavefronts, then we find a horn the mouth of which curves back as for the Kugelwellen. I called this a "revisited Tractrix" horn."
To say that the cut off frequency of a horn is related to the (mean) diameter of its mouth is a common mistake.
In fact whatever the length of a horn having a known expansion, its cut-off is the same , BUT what differs is the ripple in the response curve which is due to the interferences between normal waves emitted by the diaphragm and propagating inside the horn with waves backreflected from the mouth to the throat.
We are still wrongly using a semi-empirical rule originating from Keele who said that the ripple due to those reflections passes through a minimum when the mouth diameter is equal to the wavelength at cut-off. This is based on a model using the false assumption that the wavefronts are plane. Further studies demonstrated that such minimum doesn't exist.
The domain of application of this rule of thumb is only for cut horns (all Salmon horns must be considered as cut horns). If you use a minimum diameter equal to the wavelength at cutoff then you obtain an "acceptable" amount of ripple in the response of the horn (acceptable for whom?).
Doing that, we link that diameter to the cut-off frequency but we cannot reverse that rule so: it is not true that the cut-off frequency is related to the diameter of the mouth.
Now, IMHO, to encouter this rippling, it is highly desirable to use quasi infinite horns like complete (= uncut) Le Cléac'h horn, complete Kugelwellen or complete Tractrix. But only the Le Cléac'h horn doesn't do any assumption on the shape of the wavefronts. In this sense it is a better design than the Kugelwellen and the Tractrix, the design of which is erroneously based on the assumption that wavefronts are spherical caps.
Best regards from Paris,
Jean-Michel Le Cléac'h
The nearest conventional (= old) profile to the Le Cléac'h profile is the Kugelwellen horn (here compared among with other profiles to the Tractrix and T = 1 Le Cléac'h horn).
Notice that the Kugelwellen follows the same logic as the Tractrix ("constant speed" translation of spherical cap wavefronts of a constant radius along the axis. The radius used for the Kugelwellen being 2 times the radius used for the Tractrix).
A main difference between the Tractrix and the Kugelwellen is that the Kugelwellen expansion is exponential all along but the expansion of the Tractrix (as I calculated it) departs from an exponential law near the mouth. If we recalculate the tractrix with a pure exponential expansion of spherical cap wavefronts, then we find a horn the mouth of which curves back as for the Kugelwellen. I called this a "revisited Tractrix" horn."
To say that the cut off frequency of a horn is related to the (mean) diameter of its mouth is a common mistake.
In fact whatever the length of a horn having a known expansion, its cut-off is the same , BUT what differs is the ripple in the response curve which is due to the interferences between normal waves emitted by the diaphragm and propagating inside the horn with waves backreflected from the mouth to the throat.
We are still wrongly using a semi-empirical rule originating from Keele who said that the ripple due to those reflections passes through a minimum when the mouth diameter is equal to the wavelength at cut-off. This is based on a model using the false assumption that the wavefronts are plane. Further studies demonstrated that such minimum doesn't exist.
The domain of application of this rule of thumb is only for cut horns (all Salmon horns must be considered as cut horns). If you use a minimum diameter equal to the wavelength at cutoff then you obtain an "acceptable" amount of ripple in the response of the horn (acceptable for whom?).
Doing that, we link that diameter to the cut-off frequency but we cannot reverse that rule so: it is not true that the cut-off frequency is related to the diameter of the mouth.
Now, IMHO, to encouter this rippling, it is highly desirable to use quasi infinite horns like complete (= uncut) Le Cléac'h horn, complete Kugelwellen or complete Tractrix. But only the Le Cléac'h horn doesn't do any assumption on the shape of the wavefronts. In this sense it is a better design than the Kugelwellen and the Tractrix, the design of which is erroneously based on the assumption that wavefronts are spherical caps.
Best regards from Paris,
Jean-Michel Le Cléac'h
Attachments
Last edited:
So these are all basically exponential horns with different mouth terminations, right. The same soup with different names 🙂