Hi!
To my knowledge the flare is defined as 1/S * dS/dx. Therefore, The flare rate of a conical horn decreases while that of the exponential horn is constant.
This can be shown by assuming flat wave fronts or simply the step wise mouth surface. which is S = pi * r**2. The radius is a linear function of the x-axis:
r = m * x + b
Set this into the equation, differentiate n and set m=1 and b=0 then you get 2x/x**2 as flare rate as an example. Correct me if my quick math is wrong.
Thank you, kind Sir 🙂
I still don't understand exactly what the definition of 'flare rate' is,
but I do see I was mistakenly thinking it meant rate of area expansion.
It is the rate of area expansion. In simple words it is defined as the relative growth of area (expressed as a factor) for a given absolute change in lenght.
Regards
Charles
Regards
Charles
In order to get a proper understanding of the concept of "flare rate", we have to distinguish between assumed plane and spherical wavefronts. Each of these assumptions yields a different flare rate.
The correct method to determine the flare rate is based on wave-front areas instead of cross-sectional areas.
The correct method to determine the flare rate is based on wave-front areas instead of cross-sectional areas.
To complicate matters further:
"The geometry that describes the shape-shifting between the throat and mouth is termed the horn flare or flare rate. This can range from a simple linear expansion (the cone) to equations using half the Greek alphabet. The simplest one that we still might find in the field is the exponential taper (or exponential-ish variations thereof)."
"The geometry that describes the shape-shifting between the throat and mouth is termed the horn flare or flare rate. This can range from a simple linear expansion (the cone) to equations using half the Greek alphabet. The simplest one that we still might find in the field is the exponential taper (or exponential-ish variations thereof)."
I dunno guys...this 'flare rate' stuff..
I get area expansion and rate of area expansion..
But I've been searching for a concrete 'flare rate' definition...still looking...
Mr McBean ?
I get area expansion and rate of area expansion..
But I've been searching for a concrete 'flare rate' definition...still looking...
Mr McBean ?
The flare rate of horns can be expressed using the general equation
Ax = At(cosh(x/xo) + T sinh (x/xo))^2
Ax = Area at x along the horn
At = Area of the throat
xo = the cut off parameter
T = the flare parameter
The T in this equation determines the family to which the horn belongs. If T = 0 the expression is that of a hyperbolic cosine. If T = 1 the horn is exponential and if T = infinity the horn is conical.
For 0 < T < 1 the horn is considered a hyperbolic cosine or cosh horn. Where 1 < T < infinity the horn is considered a hyperbolic sine or sinh horn.
With lower values of T the horn flares less rapidly near the throat and provides better loading down to the cut off frequency, but also has a higher reactive component at the cut off frequency. The lower expansion rate also means that distortion caused by the horn will be greater than with that of an exponential or conical horn.
The value of T is also one of the variables in determining reactance annulling when trying to achieve maximum power transfer.
Ax = At(cosh(x/xo) + T sinh (x/xo))^2
Ax = Area at x along the horn
At = Area of the throat
xo = the cut off parameter
T = the flare parameter
The T in this equation determines the family to which the horn belongs. If T = 0 the expression is that of a hyperbolic cosine. If T = 1 the horn is exponential and if T = infinity the horn is conical.
For 0 < T < 1 the horn is considered a hyperbolic cosine or cosh horn. Where 1 < T < infinity the horn is considered a hyperbolic sine or sinh horn.
With lower values of T the horn flares less rapidly near the throat and provides better loading down to the cut off frequency, but also has a higher reactive component at the cut off frequency. The lower expansion rate also means that distortion caused by the horn will be greater than with that of an exponential or conical horn.
The value of T is also one of the variables in determining reactance annulling when trying to achieve maximum power transfer.
Kolbrek:
"You must consider the flare rate of the horn, which is defined as (rate of change of wave-front area with distance)/(wave-front area).
In a conical horn, the flare rate changes throughout the horn, and the point where propagation changes from reactive to resistive changes with frequency throughout the horn. In an exponential horn, the flare rate is constant. Here the transition from reactive to resistive wave propagation happens at the same frequency throughout the entire horn. This is the cutoff frequency. There is no gradual transition, no frequency dependent
change in propagation type, and that’s why the change is so abrupt."
"You must consider the flare rate of the horn, which is defined as (rate of change of wave-front area with distance)/(wave-front area).
In a conical horn, the flare rate changes throughout the horn, and the point where propagation changes from reactive to resistive changes with frequency throughout the horn. In an exponential horn, the flare rate is constant. Here the transition from reactive to resistive wave propagation happens at the same frequency throughout the entire horn. This is the cutoff frequency. There is no gradual transition, no frequency dependent
change in propagation type, and that’s why the change is so abrupt."
Hi Mark,
My apologies for any confusion I may have caused. I use the term 'flare rate' when referring to the physical profile of a horn, and 'expansion rate' when referring to the change in surface area of sound wavefronts inside the horn.
Kind regards,
David
The reason I think this way is because the cross-sectional area S at any point x along the axis of an exponential horn, for example, is given by:
S = S1 * Exp(m * x)
Where m is defined as the flare (or flaring) constant, and S1 is the throat cross-sectional area (at x = 0).
References:
Olson - "Acoustical Engineering"
Beranek - "Acoustics"
Last edited:
Another reason for considering flare to be related to the physical profile of the horn:
"A horn is also a directivity controlling device, which radiates over an angle defined by the flare angle of the mouth."
Ref: Beranek & Mellow - "Acoustics - Sound Fields and Transducers"
This is why Hornresp continues to use the term "flare tangent angle".
"A horn is also a directivity controlling device, which radiates over an angle defined by the flare angle of the mouth."
Ref: Beranek & Mellow - "Acoustics - Sound Fields and Transducers"
This is why Hornresp continues to use the term "flare tangent angle".
Attachments
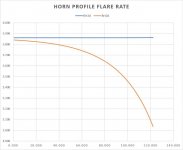
This is the flare rate of an spherical wave horn with T=1 for the 3D construction wave front flrt3d and the 2D step wise mouth surface area (numerically evaluated from the profile). flrt3D is of course constant as the derivative of the exponential function is again the exponential function.
Exact formula is: 1/S * dS/dx
Exact formula is: 1/S * dS/dx
Therefore:
m = Log(S / S1) / x
Or when expressed in terms of radius:
m = 2 * Log(R / R1) / x
Thanks for these. Along with the precise mathematical relationships that you and others have provided and which I also appreciate, some hints of why flare rate matters!
May I add my thanks to All...….David, Pooh, docali, Ro808, Charles, Jack....
Digging through terminology usage, I often find to be one of the biggest challenges in understanding...
….thank goodness for math, which I seldom understand either 😱😀
Happy Holidays Everyone ! mark
Digging through terminology usage, I often find to be one of the biggest challenges in understanding...
….thank goodness for math, which I seldom understand either 😱😀
Happy Holidays Everyone ! mark
Happy holidays !
In a blogpost on hornspeakersystems.info, Thomas Dunker recommends a book "to anyone interested in the history of engineering and technology, and of course in particular the history of the unique engineering environment that prevailed at the Bell (Telephone) Laboratories for so many years."
You can get it here, if you want to read it over the holidays.
In a blogpost on hornspeakersystems.info, Thomas Dunker recommends a book "to anyone interested in the history of engineering and technology, and of course in particular the history of the unique engineering environment that prevailed at the Bell (Telephone) Laboratories for so many years."
You can get it here, if you want to read it over the holidays.
Flare Rate
Thanks docali and Ro808 (and Dr Kolbrek), I think I might have learnt something new today… 🙂.
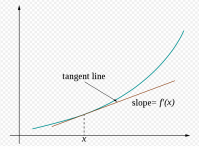
Without giving it any thought, I had automatically assumed that the flare rate at a given point on a flaring profile would simply be the first derivative, or instantaneous rate of change of the curve at that point. In other words, the slope or gradient of the tangent line to the curve at that point, as illustrated in the attachment. It seems that I was wrong in assuming this!
My sincere apologies to everyone for my earlier, now "fake news" posts on the matter. I will try to make sure that it doesn't happen again 🙂.
Thanks docali and Ro808 (and Dr Kolbrek), I think I might have learnt something new today… 🙂.
Without giving it any thought, I had automatically assumed that the flare rate at a given point on a flaring profile would simply be the first derivative, or instantaneous rate of change of the curve at that point. In other words, the slope or gradient of the tangent line to the curve at that point, as illustrated in the attachment. It seems that I was wrong in assuming this!
My sincere apologies to everyone for my earlier, now "fake news" posts on the matter. I will try to make sure that it doesn't happen again 🙂.
Attachments
Hi docali,
Just to clarify - are 'flare' and 'flare rate' the same thing, both defined as 1/S * dS/dx?
If not, would you know the definition for flare, as distinct from flare rate?
Thanks.
I was wondering if perhaps the relationship between flare and flare rate was similar to that between velocity and acceleration...
The discussion on flare has been very interesting and informative - I have never had a reason to think about such things before now. Thank you for your valuable input.
Kind regards,
David
Just to clarify - are 'flare' and 'flare rate' the same thing, both defined as 1/S * dS/dx?
If not, would you know the definition for flare, as distinct from flare rate?
Thanks.
I was wondering if perhaps the relationship between flare and flare rate was similar to that between velocity and acceleration...
The discussion on flare has been very interesting and informative - I have never had a reason to think about such things before now. Thank you for your valuable input.
Kind regards,
David