Err, have not found much on that topic on the Forum. At least not so many posts. (sigh)
One of the beautiful aspects of hollow state, as PRR calls it, brought out briefly by Bill Whitlock recently in a post after Schimel's yet-another-tubes-versus-transistors piece on an Electronic Design site, is that tubes are (I would say "almost") entirely free of capacitance variation with terminal voltages. Not sure if ML's representation captures that distinction or not.
Tony, not sure if you mean me but here is the Schimel piece link and various comments including from yours truly: ?House of Fire?: Firebottles And Groove Tubes Versus Devices That Find Their Origins in Sand (Part 1)
Brad
Brad
Yeah, except that it isn't...
Lets observe an example circuit with actual equal impedances.
Under normal conditions, both output a 10V sine.
But short either X1 or X2 jumper to the grounding cap,
and note the consequence seen at the other output!
No matter which you short, the other spits out a 15V sine.
Thats proof of the pudding right there... No favoritism.
Little distorted, far from optimally biased, but equal...
-------------
+/- 10x gains? im not sure why it isn't closer to +/- 18x,
which would be closer to Mu/2. Bad loadline I suppose.
Example in post #55 might be harder to grasp, but runs
the triode at almost constant current for true Mu/2.
I also goofed when second guessing my own earlier circuit.
1/Mu was the correct answer. 2/Mu might make the waves
a tiny bit more equal in the matched load state, but only
1/Mu cathode feedback makes the fully off-balance loads
deliver equal consequence to the other side.
-------------
There can't be any math that ignores what happens the
other side. You can't know RP or RC without knowing
how the other is loaded, because it has consequences
that must transfer for the impedances to be equal!
Actually, you see under stress they become UNEQUAL.
But the misbehavior is equally distributed, and favors
neither end... Unfortunately the best balance you can
hope to achieve, without reducing both to zero by the
global feedback method...
Attachments
In fact, you've proven my earlier point that some here insist on folding the trans-impedance from cathode to plate with Zp. Consider carefully what you quoted:
Moreover, the model that I sketched in the attachment to #254 gives exactly the result you describe above while holding Zp, Zk, and the trans-impedances constant, thus calling into question your conclusion.
I've simulated a simple small-signal model of a phase-splitter with Rp = Rk = 22k, mu = 100, rp = 62.5k. From this model, I calculated and verified the Z parameters of the coupled output ports:
Zp = 21.79k
Zk = 806.0
Zkp = -21.194k
Zpk = -210
The small-signal model and the model I sketched in the attachment give identical results including the effect you described above thus verifying the model and its interpretation.
Also, note that Zp + Zkp = Zk + Zpk = 596
Not coincidentally, 596 is the differential output impedance so it all hangs together. Just as I wrote before, my model will give the correct results (in the context in which it was derived) regardless of the loading. I has to, it's based on sound EE fundamentals.
Last edited:
You can ignore the other end only if both of your "equal" impedances are zero.
What happens at one zero node has no consequence at the other. And doesn't
matter what common or differential reference you compare to.
If only one of the two nodes is near zero (like a normal cathode), then nearly
all current consequences of voltage error at the cathode end push to the plate.
And very little (1/Mu) voltage error at the plate is pushed back as a current of
consequence to the cathode. When an arbitrary current is injected by an error
seen only at the other end that has a significant correlation to local error, how
can we possibly separate this mess to figure the local Z??? It would be simple
to ignore if it were completely uncorrelated, but its not cooperating that way.
If you design for two impedance, each close to half the typical plate resistance.
Both ends respond to voltage error, and both fight a tug of war to resolve this.
But unequal loads are also unequal anchors for current, each pushes or pulls the
consequence of voltage error from unequal footing.
Then you deal with a situation where the nodes can and must interact. Its much
more difficult to say where is the reference point? It drifts between them as any
loads that require non-linear current vs voltage attempt to throw off the balance.
Its not staying in one convenient place for you to make this calculation.
One must choose GND as the absolute reference, if only because the other way
is going to result in full tentacled insanity and an early grave...
What happens at one zero node has no consequence at the other. And doesn't
matter what common or differential reference you compare to.
If only one of the two nodes is near zero (like a normal cathode), then nearly
all current consequences of voltage error at the cathode end push to the plate.
And very little (1/Mu) voltage error at the plate is pushed back as a current of
consequence to the cathode. When an arbitrary current is injected by an error
seen only at the other end that has a significant correlation to local error, how
can we possibly separate this mess to figure the local Z??? It would be simple
to ignore if it were completely uncorrelated, but its not cooperating that way.
If you design for two impedance, each close to half the typical plate resistance.
Both ends respond to voltage error, and both fight a tug of war to resolve this.
But unequal loads are also unequal anchors for current, each pushes or pulls the
consequence of voltage error from unequal footing.
Then you deal with a situation where the nodes can and must interact. Its much
more difficult to say where is the reference point? It drifts between them as any
loads that require non-linear current vs voltage attempt to throw off the balance.
Its not staying in one convenient place for you to make this calculation.
One must choose GND as the absolute reference, if only because the other way
is going to result in full tentacled insanity and an early grave...
Last edited:
Alfred Centauri, I'm having difficulty following your handwritten notes. What is the symbol that looks kind of like a backwards letter xi?
EDIT: Is it the inverse of gm? If so, perhaps the theory can be written in a less obfuscated way; everyone is familiar with gm.
EDIT: Is it the inverse of gm? If so, perhaps the theory can be written in a less obfuscated way; everyone is familiar with gm.
Last edited:
Correction, I did not simulate your example circuit but rather a simple phase splitter. The perils of posting before morning coffee... ;^)
Later today, I'll work on extracting the Z parameters of your example circuit and compare those to the simple phase splitter.
I suspect that the Zp and Zk will be more less equal as will be the trans-impedances which implies the results you describe.
Later today, I'll work on extracting the Z parameters of your example circuit and compare those to the simple phase splitter.
I suspect that the Zp and Zk will be more less equal as will be the trans-impedances which implies the results you describe.
kenpeter, since you already have your example circuit working in your simulator, why don't you extract the Z parameters for my model. It's easy to do.
Replace R6 and R7 with AC current sources; label them I6 and I7. Initially, zero both. Set the AC voltage of V2 to 1 and plot the AC voltages across the current sources. The midband values are the open circuit voltage gain parameters, Ap (across I6) and Ak (across I7).
Now, zero the AC voltage on V2. Set the AC voltage of I6 to 1 and plot the voltages across the current sources again. The midband values are the Zp (across I6) and Zpk (across I7) parameters.
Now, zero I6 and set I7 to 1 and plot the voltages across the current sources again. The midband values are the Zkp (across I6) and Zk (across I7).
That's it. Let me know what they are and I'll plug them into my model and see if we get comparable results.
Replace R6 and R7 with AC current sources; label them I6 and I7. Initially, zero both. Set the AC voltage of V2 to 1 and plot the AC voltages across the current sources. The midband values are the open circuit voltage gain parameters, Ap (across I6) and Ak (across I7).
Now, zero the AC voltage on V2. Set the AC voltage of I6 to 1 and plot the voltages across the current sources again. The midband values are the Zp (across I6) and Zpk (across I7) parameters.
Now, zero I6 and set I7 to 1 and plot the voltages across the current sources again. The midband values are the Zkp (across I6) and Zk (across I7).
That's it. Let me know what they are and I'll plug them into my model and see if we get comparable results.
Merlinb, the symbol in question is just a lowercase, cursive 'z'. It represents the transfer impedance. Although the transfer impedances are a function of gm, they're not equal to 1/gm.
In words, the transfer-impedance Zkp it is the ratio of the open-circuit AC output voltage at the plate to the AC current out of the cathode output. Google "Z parameters" or open-circuit parameters for more general details.
If my algebra is correct:
Zkp = -(1 + mu)*Rk*Rp / [rp + Rp + (1 + mu)*Rk]
Zpk = -[(Rp - Rk)*rp + Rp*Rk] / [rp + Rp + (1 + mu)*Rk]
When Rp = Rk: Zkp = (1 + mu)*Zpk
...
Zp and Zk are the well known:
Zp = [rp + (1 + mu)*Rk] || Rp
Zk = Rk || [(rp + Rp) / (1 + mu)]
...
The open-circuit gains, Ap & Ak, are the well-known:
Ap = -mu*Rp / [rp + Rp + (1 + mu)*Rk]
Ak = mu*Rk / [rp + Rp + (1 + mu)*Rk]
In words, the transfer-impedance Zkp it is the ratio of the open-circuit AC output voltage at the plate to the AC current out of the cathode output. Google "Z parameters" or open-circuit parameters for more general details.
If my algebra is correct:
Zkp = -(1 + mu)*Rk*Rp / [rp + Rp + (1 + mu)*Rk]
Zpk = -[(Rp - Rk)*rp + Rp*Rk] / [rp + Rp + (1 + mu)*Rk]
When Rp = Rk: Zkp = (1 + mu)*Zpk
...
Zp and Zk are the well known:
Zp = [rp + (1 + mu)*Rk] || Rp
Zk = Rk || [(rp + Rp) / (1 + mu)]
...
The open-circuit gains, Ap & Ak, are the well-known:
Ap = -mu*Rp / [rp + Rp + (1 + mu)*Rk]
Ak = mu*Rk / [rp + Rp + (1 + mu)*Rk]
I can put the current sources easy enough, but I don't have the
slightest understanding of your intent for me to do with them?
These are gonna be at some different frequency than the forward
path through the splitter, so we can see which levels at each node
belong to each stimulus on an FFT??? Otherwise, I don't get it.
They are gonna intermodulate too, I would expect...
You can take any sim I posted and prove whatever you like with it.
Might be easier than trying to explain to me how to do this thing?
I can't quite warp my random thought process around it just yet.
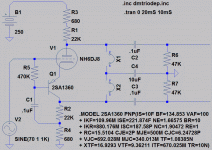
You only need .asc what was posted at #286, and dmtriodep.inc
from Duncan Amps websight... The Toshiba transistor .model is
built into the simulation, Homemodder posted it sometime back,
so you won't need to go searching for that one...
It could work a lot better with a bias that was more adjustible.
The one resistor bias was only for simplicity, not good function.
Right now, it can't and won't bias to the best part of the loadline.
Correcting the bias was beyond the scope of the small point I
was trying to get across. But my non-linearity might IMD your
proposed test too much, you might take a crack at fixing it...
It might not be a problem if your test can be done with small
enough levels that don't much challenge the poor linearity.
slightest understanding of your intent for me to do with them?
These are gonna be at some different frequency than the forward
path through the splitter, so we can see which levels at each node
belong to each stimulus on an FFT??? Otherwise, I don't get it.
They are gonna intermodulate too, I would expect...
You can take any sim I posted and prove whatever you like with it.
Might be easier than trying to explain to me how to do this thing?
I can't quite warp my random thought process around it just yet.
You only need .asc what was posted at #286, and dmtriodep.inc
from Duncan Amps websight... The Toshiba transistor .model is
built into the simulation, Homemodder posted it sometime back,
so you won't need to go searching for that one...
It could work a lot better with a bias that was more adjustible.
The one resistor bias was only for simplicity, not good function.
Right now, it can't and won't bias to the best part of the loadline.
Correcting the bias was beyond the scope of the small point I
was trying to get across. But my non-linearity might IMD your
proposed test too much, you might take a crack at fixing it...
It might not be a problem if your test can be done with small
enough levels that don't much challenge the poor linearity.
Last edited:
Essentially, you'll run three different AC sweeps on your circuit (from 100Hz to 10kHz will be fine). You need three AC sources: V2, I6 (replaces R6) and I7 (replaces R7). Only one of these sources will be activated during each of the three AC sweeps; it will have an AC value of 1. The other two will be set to zero AC volts or amps.
In all three sweeps, you'll be plotting the output voltages, the voltages across I6 and I7.
In this way, you see the AC response of the outputs to each of the different sources, one at a time.
These responses tell us the 6 parameters in my model: Ap, Ak, Zp, Zk, Zkp, Zpk. You read the magnitudes directly from the output voltages.
I'm having trouble simulating your circuit for some reason. I'm coming up with screwy parameter values and I would like to see what you're getting.
What simulator are you using? Does it work on Linux?
In all three sweeps, you'll be plotting the output voltages, the voltages across I6 and I7.
In this way, you see the AC response of the outputs to each of the different sources, one at a time.
These responses tell us the 6 parameters in my model: Ap, Ak, Zp, Zk, Zkp, Zpk. You read the magnitudes directly from the output voltages.
I'm having trouble simulating your circuit for some reason. I'm coming up with screwy parameter values and I would like to see what you're getting.
What simulator are you using? Does it work on Linux?
LTSpice. Linux, Wine, I don't know???
Copy and paste from helpfile:
----------------------------------
Running Under Linux
Do you have a Linux version of this program?
Not a separate edition, but it does run under WINE. The program has been tested on Linux RedHat 8.0 with WINE version 20030219, RedHat 9.0 with WINE 20040716, and SuSE 9.1 with 20040716.
------------------------------------
Also don't put much more than 2VPP at 70VDC into the input.
Unlike a normal concertina, this one has gain, and clips bad
enough to hang the sim with the usual input levels.
Copy and paste from helpfile:
----------------------------------
Running Under Linux
Do you have a Linux version of this program?
Not a separate edition, but it does run under WINE. The program has been tested on Linux RedHat 8.0 with WINE version 20030219, RedHat 9.0 with WINE 20040716, and SuSE 9.1 with 20040716.
------------------------------------
Also don't put much more than 2VPP at 70VDC into the input.
Unlike a normal concertina, this one has gain, and clips bad
enough to hang the sim with the usual input levels.
Last edited:
OK, in the meantime I figured out that it's LTSpice which I actually already have installed. I runs fine in Wine but I essentially have no experience with this program.
Nonetheless, I simulated your circuit and extracted the following parameters:
Ap = -11.72
Az = 11.65
Zp = 14.81k
Zk = 14.44k
Zpk = -8.245k
Zkp = -8.268k
So, as I suspected it must be, the Zp and Zk (open-circuit output impedances) are nearly equal as are the transfer impedances for your circuit.
So, according to this, the differential mode output impedance should be about
Zp + Zpk = 6.57k. Let's see...
Yep, with R6 and R7 set to 6.57k, I'm seeing an output voltage roughly half the open-circuit output voltage from both your circuit and my model Z parameter model of it.
Cool!
Nonetheless, I simulated your circuit and extracted the following parameters:
Ap = -11.72
Az = 11.65
Zp = 14.81k
Zk = 14.44k
Zpk = -8.245k
Zkp = -8.268k
So, as I suspected it must be, the Zp and Zk (open-circuit output impedances) are nearly equal as are the transfer impedances for your circuit.
So, according to this, the differential mode output impedance should be about
Zp + Zpk = 6.57k. Let's see...
Yep, with R6 and R7 set to 6.57k, I'm seeing an output voltage roughly half the open-circuit output voltage from both your circuit and my model Z parameter model of it.
Cool!
What do you make of this one with current gain?
The cathode operates near ground, and the plate current
is an almost constant 3.3mA. For a much better loadline.
It still freaks out on A2, I need to do something like
Wavy's Pyramid to keep DC from pumping out of control.
Just making equal Z's with huge current available don't
automatically let you run A2. Damn thing pumps!!!
He made impedances especially unequal at DC, even with
the global loop closed (was there a global loop? I don't
remember). And ref'd both output grid DC to his cathode.
Anyawys, thats what it needs. Transistion to unequal Z
somewhere between 20 and DC, and DC ref both output
grids to the cathode end.
The cathode operates near ground, and the plate current
is an almost constant 3.3mA. For a much better loadline.
It still freaks out on A2, I need to do something like
Wavy's Pyramid to keep DC from pumping out of control.
Just making equal Z's with huge current available don't
automatically let you run A2. Damn thing pumps!!!
He made impedances especially unequal at DC, even with
the global loop closed (was there a global loop? I don't
remember). And ref'd both output grid DC to his cathode.
Anyawys, thats what it needs. Transistion to unequal Z
somewhere between 20 and DC, and DC ref both output
grids to the cathode end.
Last edited:
The differential (plate-cathode) impedance of about 2/gm is quite proper to use when the loads are balanced, such as when no output tube grid currents are flowing. But this does not mean that the plate impedance equals the cathode impedance. The plate to ground impedance is much higher than the cathode to ground impedance, even if the loads are pefectly balanced.
Nobody disagrees with that, I don't think? But legacy
different impedance Cathodyne is like so 5min ago...
That problem has already been fixed and proved fixed.
Plate and Collector impedance can be same, both
under the voltage control of a single triode...
Move on to DC pumping when output grids conduct.
How best to do this without adding followers? Was
the Pyramid close to an optimal answer? How do we
adapt equal Z design to the Pyramid?
different impedance Cathodyne is like so 5min ago...
That problem has already been fixed and proved fixed.
Plate and Collector impedance can be same, both
under the voltage control of a single triode...
Move on to DC pumping when output grids conduct.
How best to do this without adding followers? Was
the Pyramid close to an optimal answer? How do we
adapt equal Z design to the Pyramid?
Last edited:
That does not accord with experiment, which is perfectly consistent with plate Thevenin source impedance equaling cathode Thevenin source impedance when the loads are equal. Merely repeating the mantra doesn't change experimental results. Alfred's analysis is more correct than yours, but is far more complex and non-intuitive for the situations where one actually uses a cathodyne- to drive identical loads, where the source impedances (and consequent poles) are equal. The best general treatment is Vogel's (a lot of equations, but simple to follow), but it's a lot of algebra expended to derive answers for situations where cathodynes aren't used.