I start this thread, because the subject of inductor linearity was raised in this discussion:
https://www.diyaudio.com/forums/equ...software-distortion-analyzer-post6199594.html
As I am also interested in the subject, I carried out some tests.
I tested three very different types of materials: a general-purpose manganese ferrite (grade 3H1), a VHF nickel ferrite (grade 4C4), and an iron-powder/polymer composite of unknown origin.
These are relatively old materials, but the data is still indicative, and more modern grades improve on saturation limit, temperature stability, HF behavior, losses -not on linearity-.
In the days of FDM telephony, linearity had some importance, but that's no longer the case.
I made the tests on X22 cores: they are convenient to work with, and I have plenty of them.
As I hate winding works, I used salvaged, already wound coil-formers as test windings.
This means that I didn't have the choice of the number of turns, but it doesn't really matter: the results have to be normalized anyway.
The tests were made for a zero airgap: what interests us is the core non-linearity for a given induction.
In an actual inductor, this non-linearity will become "diluted" by various factors, but by knowing the source value, it is possible to compute the non-linearity for any situation.
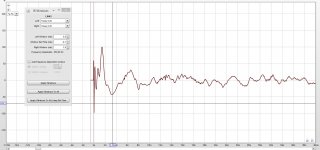
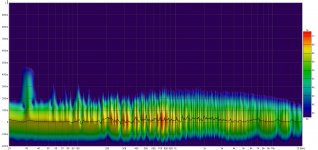
Here is the test-jig for the 3H1:
The 1K series resistor is calculated to be ~equal to the reactance of the inductor at the test frequency. It will be the load seen by the harmonics generated by the coil.
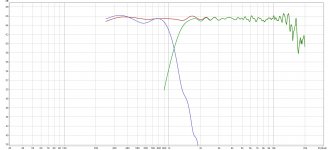
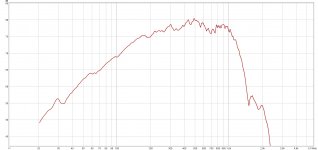
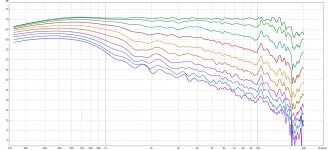
The test voltage was varied from 72mV to 2.2Vrms, resulting in a peak induction comprised between 1.293mT and 39.5mT.
Here are the results:
Code:
^B(mT) k(%)
1.293 0.023
3.95 0.062
12.93 0.175
39.5 0.45
There seems to be a quasi-linear dependency of the non-linearity with the excitation level.
These raw figures will be reduced if an airgap is added.
This is the equivalent circuit with an airgap: the reluctances on the left, and the electrical equivalent on the right.
It is obvious that by making Lgap much smaller than Lcore, the THD will be reduced in the same proportion.
Lgap can be computed : n²*
µo*Ae/d (Ae= effective area, d= airgap).
The distortion will also be reduced if the excitation level is reduced.
It is counter-intuitive, but adding a gap will not directly reduce the induction: the induction formula does not include any magnetic parameter.
However if the gap is increased, the inductance will decrease and if the excitation voltage and frequency are kept identical, the current will increase, and the greater H will compensate exactly the increased reluctance.
Of course, in general the coil will be adapted to keep the same value with an increased airgap: this means increasing the number of turns by √r, and this will reduce the induction.
Here is a pic of the cores tested:
The 4C4 cores are clamped by a nylon bolt, but the 3H1's have a threaded insert and require an external clamp (or the proper mounting hardware).
The iron-powder core is an horrible kludge, more on that later













![URL]](/community/proxy.php?image=http%3A%2F%2F%5BURL%3D%22https%3A%2F%2Fwww.lajazz.jp%2Fimages%2FAudio%2FDH%2FAltec_820%2FAltec_820_Obi1.jpg%22%5Dhttps%3A%2F%2Fwww.lajazz.jp%2Fimages%2FAudio%2FDH%2FAltec_820%2FAltec_820_Obi1.jpg%5B%2FURL%5D&hash=7864bc75ef3032bd711beda5c5430f4e)