Denafrips ARES II board repair
- By mattworld
- Digital Line Level
- 4 Replies
I just got a spare Denafrips ARES II board. I bought it used ("in working condition") but I doubt it is the case. The initial plan was to use it in a DIY DAC perhaps with a lithium battery power supply. But first I need to power-up this board, repair it and test it. Can you help me with that ?
I am looking for information about the original transformer and how it is wire on the board (PIN 1 to 8) ?
Here is the top of the board:
I already see two problems on the board :
I am looking for information about the original transformer and how it is wire on the board (PIN 1 to 8) ?
Here is the top of the board:
I already see two problems on the board :
The two center PIN of the chip (red arrow) were connected. Any clue of the chip reference ? I think it is a LDO fix the gate voltage the transistor. | On the LT1763 LDO seems defected (yellow, too much heat) |
Attachments
Woden Empress of India, BVR for Alpair 12pw
- By planet10
- Planet 10 hifi
- 11 Replies
Big Vent Relex for the Mark Audio Alpair 12pw. Comment from builder (he may chip in)
Contach me or Scott about getting acess to the full planset.
dave
Contach me or Scott about getting acess to the full planset.
dave
Digital level meter for R-R tape deck
- By Leoniv
- Analogue Source
- 5 Replies
The analog level meter has been designed for use as a recording level meter for a reel to reel tape recorder. But it can also be used as a standalone device. The LED bar can contain up to 50 elements per channel. To reduce the level of interference, static indication is used. A feature of the meter is fully digital signal processing. That allows you to make the meter metrologically accurate, with an exact match of the dynamic characteristics. All parameters are programmed using special software on a computer.
Each meter channel contains two signal processing branches, the readings of the first one are displayed as a bar, the second - as a dot. This can be used to display two values, such as average + quasi-peak, or quasi-peak + true peak. For each of the branches, you can individually set the gain, integration time, response time, decay time, hold time, fall time, peak hold time, peak fall time. The scale type is set by assigning an individual threshold level to each LED with an accuracy of 0.01 dB. This allows you to build a linear, logarithmic, S-shaped with a stretch near 0 dB and other scales. A set of all parameters, including the scale type, is stored in EEPROM as a preset. There can be 4 different presets in total. They can be selected with the control button. The second button can turn on the indication of statistics of maximum levels, as well as reset it.
Here we will talk about how simple things can be made difficult 🙂
Block diagram
The block diagram of the level meter is shown in the figure below. This diagram shows one stereo channel of the meter. The input signal is fed to a differential amplifier implemented on an op-amp (Meter50_v4_sch.pdf). It performs two tasks: it shifts the signal by half the ADC scale and allows you to implement a balanced input. The signal shift is necessary because the built-in ADC is unipolar, its input range is from 0 to the reference voltage. A balanced input is desirable even if the signal source is single ended. It allows you to take the signal relative to "analogue" ground and eliminate the interference present on the ground of the meter circuit. If the level meter is made as a separate device, then balanced inputs with XLR connectors can be implemented.
All signal processing is done digitally by the STM32F100/103 microcontroller. To avoid the use of an anti-alias filter at the ADC input, as well as to be able to register short signal peaks, the sampling frequency was chosen quite high - 96 kHz. With DMA, ADC samples are stored in a buffer in RAM. When half of the array is ready, an interrupt occurs, the data is read and processed.
DC removal filter
The first operation on digital data is to remove the DC component from the signal. This must be done before the signal is sent to the detector. With a meter dynamic range of about 60 dB, even such a small DC component as 0.1% of the ADC scale can be equal in magnitude to the useful signal and distort it.
Detector
Next, a full-wave rectification of the signal is performed. This is the easiest part of processing. When the DC component is removed from the signal, the task is to calculate the absolute value.
Filters
Next are several filters that define the dynamic characteristics of the meter.
Integration time
To obtain a given integration time, the detector output must be smoothed with a filter. The smoothing filter is not a simple low-pass filter, but a more complex filter with different charge and discharge time constants. The charge must be fast to provide the specified meter integration time. And the discharge must occur slowly to provide a given return time, which is much longer. Therefore, the integration time filter is turned on only when the signal rises; when the signal decreases, it is kept at the same level. A separate filter is used for signal decay.
The difference filter equation has the following form:
y( n ) = y(n-1) + A*(x( n ) - y(n-1)), where A = 0.0083 for Fs = 96 kHz
A 32-bit accumulator is used to obtain the required calculation accuracy. Filter coefficients are 16-bit unsigned. They are defined as A = 65536 / 96000 / tau.
Each meter channel contains two signal processing branches, the readings of the first one are displayed as a bar, the second - as a dot. This can be used to display two values, such as average + quasi-peak, or quasi-peak + true peak. For each of the branches, you can individually set the gain, integration time, response time, decay time, hold time, fall time, peak hold time, peak fall time. The scale type is set by assigning an individual threshold level to each LED with an accuracy of 0.01 dB. This allows you to build a linear, logarithmic, S-shaped with a stretch near 0 dB and other scales. A set of all parameters, including the scale type, is stored in EEPROM as a preset. There can be 4 different presets in total. They can be selected with the control button. The second button can turn on the indication of statistics of maximum levels, as well as reset it.
Here we will talk about how simple things can be made difficult 🙂
Block diagram
The block diagram of the level meter is shown in the figure below. This diagram shows one stereo channel of the meter. The input signal is fed to a differential amplifier implemented on an op-amp (Meter50_v4_sch.pdf). It performs two tasks: it shifts the signal by half the ADC scale and allows you to implement a balanced input. The signal shift is necessary because the built-in ADC is unipolar, its input range is from 0 to the reference voltage. A balanced input is desirable even if the signal source is single ended. It allows you to take the signal relative to "analogue" ground and eliminate the interference present on the ground of the meter circuit. If the level meter is made as a separate device, then balanced inputs with XLR connectors can be implemented.
All signal processing is done digitally by the STM32F100/103 microcontroller. To avoid the use of an anti-alias filter at the ADC input, as well as to be able to register short signal peaks, the sampling frequency was chosen quite high - 96 kHz. With DMA, ADC samples are stored in a buffer in RAM. When half of the array is ready, an interrupt occurs, the data is read and processed.
DC removal filter
The first operation on digital data is to remove the DC component from the signal. This must be done before the signal is sent to the detector. With a meter dynamic range of about 60 dB, even such a small DC component as 0.1% of the ADC scale can be equal in magnitude to the useful signal and distort it.
The simplest filter that suppresses the DC component is the differentiator. It has one zero at zero frequency. The DC gain is zero (as required), and as the frequency increases, the gain increases. For a discrete implementation of the differentiator, its difference equation has the following form:
y( n ) = x( n ) – x(n-1)
In fact, this is the simplest FIR filter. When implementing, it must be taken into account that the output value must have a width of at least 1 bit more than the input value. Since the input signal in theory in one cycle can change to the full scale. Increasing the gain with increasing frequency is not satisfactory, since the gain will change in the operating frequency range. Instead, you need to get a linear frequency response above a certain cutoff frequency. Obviously, this requires adding a pole at the desired cutoff frequency. This can be done by connecting the differentiator and the 1st order low-pass filter in series. The overall frequency response will have the desired form. Such a 1st-order low-pass filter in such applications is often called a "leaky integrator". Because in the analog version, such an integrator is implemented by adding a resistor in parallel with the capacitance, through which it will slowly discharge. For a discrete implementation, the difference equation of an ideal integrator is given below:
y( n ) = y(n-1) + x( n )
To add a leakage, you need to multiply the accumulated value by some coefficient less than one:
y( n ) = A*y(n-1) + x( n ), 0 < A < 1
This is the simplest IIR low pass filter. The name "leaky integrator" is used to indicate that this filter is applied in a somewhat unusual way - the operating frequency band lies in the stopband.
The cutoff frequency here should be chosen low compared to the sampling rate, which means that the A coefficient should be close to unity. The cutoff frequency can be calculated using the equation:
f = (1 - A)*Fs/2*pi, or A = 1 – 2*pi*f/Fs, where Fs is the sampling frequency.
The general difference equation for the filter will look like this:
y( n ) = x( n ) – x(n-1) + A*y(n-1)
In fact, this is a first-order IIR high-pass filter. It is equivalent to a differentiating RC chain. Such a filter has one zero and one pole. If you show them on the z-plane, then zero will lie at the point z=1, and a little to the left of it on the axis there will be a pole.
The audio bandwidth starts at 20 Hz. But it is desirable to make the cutoff frequency lower so that a noticeable phase shift does not appear in the audio band. This filter is not phase-linear, so signal components of different frequencies will be delayed for different times. The result of their addition will give a different waveform, the peak level will be incorrect. There are phase-linear FIR high-pass filters, but they require a lot of computing resources to obtain good linearity of the frequency response in the passband at a low cutoff frequency. There is a filter option for removing DC component based on MAF (moving average filter). It doesn't use much computational resources, but it does require a lot of memory to get a high sample rate to cutoff frequency ratio.
In this case, the requirements for the filter are not very strict. It is necessary to remove the DC voltage, which can only change very slowly (for example, due to the temperature drift of the op-amp). A significant part of the compensated bias is generally constant, as it is associated with the error of the bias voltage divider. Therefore, you can simply make the cutoff frequency lower, while minimizing the phase shift. A cutoff frequency of about 5 Hz would be a good choice. The phase shift at a frequency of 20 Hz will be about 17 degrees, which can be considered acceptable.
When implementing a filter in integer arithmetic, one must take care of the ranges of numbers at all stages of the calculation so that overflow does not occur. The leaky integrator and differentiator can be connected in any order. But to avoid overflow, the differentiator should be included first.
Another problem, more complex, is related to rounding errors. For a filter cutoff frequency of 5 Hz at a sampling rate of 96 kHz, the value of the coefficient A = 0.999673. To carry out calculations with such a coefficient with good accuracy, it is required to increase the bit depth. The reverse transition will be a quantization with a larger step, which leads to the appearance of an error, or quantization noise. As a result of such an error in the filter, a parasitic constant component may appear at the output, which is even greater than the one that is suppressed. This error may cause the filter to fail. As a practical test has shown, the filter does not actually work without requantization error correction.
In this case, the ADC is 12-bit, the samples are placed in 16-bit signed integers. Some margin is needed here to protect against overflow. Multiplication is done in 32-bit format. Then, when moving from a 32-bit intermediate result to a 16-bit result, a quantization error will occur. In one of the publications it is proposed to add a quantization noise spectrum shaper to the filter by introducing error feedback. The implementation of this method is very simple. I made my own implementation which uses the same error correction principle.
static const double POLE = 0.999673;
static const int32_t A = (int32_t)(UINT16_MAX * POLE);
static int32_t acc = 0;
static int16_t xx = 0;
static int16_t yy = 0;
x = Input;
acc = LO_W(acc) + A * yy;
yy = x - xx + HI_W(acc);
xx = x;
Output = yy;
Quantization occurs by discarding the lower half of the 32-bit number. The discarded value is the quantization error. The original number is signed, but the error is always negative. For example, if the least significant bits of a positive number are replaced with zeros, the number will decrease, and some positive number will have to be added to correct the error. If the least significant bits of a negative number are replaced by zeros, the number will become large in absolute value, while remaining negative. This means that in order to correct the error, you will again need to add some positive number. Therefore, the error can be extracted from the original 32-bit number by simply zeroing its high half along with the sign bit.
y( n ) = x( n ) – x(n-1)
In fact, this is the simplest FIR filter. When implementing, it must be taken into account that the output value must have a width of at least 1 bit more than the input value. Since the input signal in theory in one cycle can change to the full scale. Increasing the gain with increasing frequency is not satisfactory, since the gain will change in the operating frequency range. Instead, you need to get a linear frequency response above a certain cutoff frequency. Obviously, this requires adding a pole at the desired cutoff frequency. This can be done by connecting the differentiator and the 1st order low-pass filter in series. The overall frequency response will have the desired form. Such a 1st-order low-pass filter in such applications is often called a "leaky integrator". Because in the analog version, such an integrator is implemented by adding a resistor in parallel with the capacitance, through which it will slowly discharge. For a discrete implementation, the difference equation of an ideal integrator is given below:
y( n ) = y(n-1) + x( n )
To add a leakage, you need to multiply the accumulated value by some coefficient less than one:
y( n ) = A*y(n-1) + x( n ), 0 < A < 1
This is the simplest IIR low pass filter. The name "leaky integrator" is used to indicate that this filter is applied in a somewhat unusual way - the operating frequency band lies in the stopband.
The cutoff frequency here should be chosen low compared to the sampling rate, which means that the A coefficient should be close to unity. The cutoff frequency can be calculated using the equation:
f = (1 - A)*Fs/2*pi, or A = 1 – 2*pi*f/Fs, where Fs is the sampling frequency.
The general difference equation for the filter will look like this:
y( n ) = x( n ) – x(n-1) + A*y(n-1)
In fact, this is a first-order IIR high-pass filter. It is equivalent to a differentiating RC chain. Such a filter has one zero and one pole. If you show them on the z-plane, then zero will lie at the point z=1, and a little to the left of it on the axis there will be a pole.
The audio bandwidth starts at 20 Hz. But it is desirable to make the cutoff frequency lower so that a noticeable phase shift does not appear in the audio band. This filter is not phase-linear, so signal components of different frequencies will be delayed for different times. The result of their addition will give a different waveform, the peak level will be incorrect. There are phase-linear FIR high-pass filters, but they require a lot of computing resources to obtain good linearity of the frequency response in the passband at a low cutoff frequency. There is a filter option for removing DC component based on MAF (moving average filter). It doesn't use much computational resources, but it does require a lot of memory to get a high sample rate to cutoff frequency ratio.
In this case, the requirements for the filter are not very strict. It is necessary to remove the DC voltage, which can only change very slowly (for example, due to the temperature drift of the op-amp). A significant part of the compensated bias is generally constant, as it is associated with the error of the bias voltage divider. Therefore, you can simply make the cutoff frequency lower, while minimizing the phase shift. A cutoff frequency of about 5 Hz would be a good choice. The phase shift at a frequency of 20 Hz will be about 17 degrees, which can be considered acceptable.
When implementing a filter in integer arithmetic, one must take care of the ranges of numbers at all stages of the calculation so that overflow does not occur. The leaky integrator and differentiator can be connected in any order. But to avoid overflow, the differentiator should be included first.
Another problem, more complex, is related to rounding errors. For a filter cutoff frequency of 5 Hz at a sampling rate of 96 kHz, the value of the coefficient A = 0.999673. To carry out calculations with such a coefficient with good accuracy, it is required to increase the bit depth. The reverse transition will be a quantization with a larger step, which leads to the appearance of an error, or quantization noise. As a result of such an error in the filter, a parasitic constant component may appear at the output, which is even greater than the one that is suppressed. This error may cause the filter to fail. As a practical test has shown, the filter does not actually work without requantization error correction.
In this case, the ADC is 12-bit, the samples are placed in 16-bit signed integers. Some margin is needed here to protect against overflow. Multiplication is done in 32-bit format. Then, when moving from a 32-bit intermediate result to a 16-bit result, a quantization error will occur. In one of the publications it is proposed to add a quantization noise spectrum shaper to the filter by introducing error feedback. The implementation of this method is very simple. I made my own implementation which uses the same error correction principle.
static const double POLE = 0.999673;
static const int32_t A = (int32_t)(UINT16_MAX * POLE);
static int32_t acc = 0;
static int16_t xx = 0;
static int16_t yy = 0;
x = Input;
acc = LO_W(acc) + A * yy;
yy = x - xx + HI_W(acc);
xx = x;
Output = yy;
Quantization occurs by discarding the lower half of the 32-bit number. The discarded value is the quantization error. The original number is signed, but the error is always negative. For example, if the least significant bits of a positive number are replaced with zeros, the number will decrease, and some positive number will have to be added to correct the error. If the least significant bits of a negative number are replaced by zeros, the number will become large in absolute value, while remaining negative. This means that in order to correct the error, you will again need to add some positive number. Therefore, the error can be extracted from the original 32-bit number by simply zeroing its high half along with the sign bit.
Detector
Next, a full-wave rectification of the signal is performed. This is the easiest part of processing. When the DC component is removed from the signal, the task is to calculate the absolute value.
Filters
Next are several filters that define the dynamic characteristics of the meter.
The main characteristics of level meters are integration time and return time. The integration time determines how quickly the meter reacts to changes in signal level. If the integration time is large (about 300 ms), the so-called VU-meter is obtained. Such a meter will not respond to short signal peaks that can overload the recording path. When pointer instruments were used as the indication device, the integration time could not be made small due to the inertia of the moving system. Therefore, often the VU-meter was combined with a faster LED peak indicator. The use of high-speed information display devices, such as gas discharge tubes or LEDs, removed the problem of obtaining short integration times and made it possible to build peak or quasi-peak meters.
Most often, quasi-peak level meters are used to measure the signal level in audio paths. Unlike true peak meters, which in theory have zero integration time, for quasi-peak meters this time is defined by the standards. It would seem that it is necessary to achieve the minimum possible integration time so that the indicator can register the shortest signal peaks without overloading the path. This approach is used in digital paths, where even a short-term overload leads to undesirable consequences. For analog magnetic recording, a short overload may not be audible at all. If you want to completely eliminate the overload at the peaks of the signal, you will have to reduce the average recording level, which will lead to a more audible problem - a decrease in the signal-to-noise ratio. Therefore, for analog magnetic recording, it makes sense to choose some optimal value for the integration time of the level meter so that it allows short-term overloads.
The integration time for quasi-peak meters is defined by IEC 60268-10 as "...the duration of a burst of sinusoidal voltage of 5000 Hz at reference level which results in an indication 2 dB below reference indication". This standard defines an integration time value of 5 ms for quasi-peak meters.
The integration time is not numerically equal to the charging time constant of the smoothing RC circuit. If an RC circuit with a charge time constant of 5 ms is installed at the output of the peak detector, then the level of -2 dB (about 0.8) will be reached in about 20 ms. To reach -2dB in 5ms, the charging time constant of the RC circuit would need to be around 1.25ms. Thus, the integration time is approximately 4 tau RC circuit.
In addition to the integration time, quasi-peak meters have a return time that is much longer. This time determines how fast the reading will fall after the signal is removed. If this time is made small (for example, equal to the integration time), then the indicator readings will change too quickly, making them difficult to read. For VU meters, such a problem did not arise due to their low speed, one time constant could be dispensed with. In high-speed quasi-peak meters, it is necessary to artificially slow down the fall in readings so that the operator can read the information.
The return time determines how quickly the meter reading will fall by 20 dB after the signal is removed. It is also not equal to the discharge time constant of the RC circuit, but is approximately 2.3 tau. The return time value is also set by the standards. It differs for indicators of different purposes. For indicators of the first type, which serve to check the signal level during its operational adjustment (this is just the case of adjusting the recording level in a tape recorder), the return time should be 1.7±0.3 sec. Accordingly, the discharge time constant of the RC circuit should be approximately 740 ms.
Level meters have another dynamic characteristic - response time. It may not be entirely clear. For inertialess devices, ballistics is artificially formed, similar to pointer devices. Increasing the response time in this case should not increase the integration time of the meter. The short signal pulses should still display correctly. To do this, the detector must "wait" until the reading reaches the measured value, and only then start the fall. In amateur designs of quasi-peak meters, with a fast increase in the signal level, the bar immediately jumps from one length to another. This is not the case with professional quasi-peak meters, because the increase in response time has a positive effect on the perception of readings by the operator. In VU meters, this is also not the case, there the smoothness of movement is obtained due to the large integration time. The response time is defined as the interval from the moment the test tone burst begins until the reading reaches -1 dB.
Most often, quasi-peak level meters are used to measure the signal level in audio paths. Unlike true peak meters, which in theory have zero integration time, for quasi-peak meters this time is defined by the standards. It would seem that it is necessary to achieve the minimum possible integration time so that the indicator can register the shortest signal peaks without overloading the path. This approach is used in digital paths, where even a short-term overload leads to undesirable consequences. For analog magnetic recording, a short overload may not be audible at all. If you want to completely eliminate the overload at the peaks of the signal, you will have to reduce the average recording level, which will lead to a more audible problem - a decrease in the signal-to-noise ratio. Therefore, for analog magnetic recording, it makes sense to choose some optimal value for the integration time of the level meter so that it allows short-term overloads.
The integration time for quasi-peak meters is defined by IEC 60268-10 as "...the duration of a burst of sinusoidal voltage of 5000 Hz at reference level which results in an indication 2 dB below reference indication". This standard defines an integration time value of 5 ms for quasi-peak meters.
The integration time is not numerically equal to the charging time constant of the smoothing RC circuit. If an RC circuit with a charge time constant of 5 ms is installed at the output of the peak detector, then the level of -2 dB (about 0.8) will be reached in about 20 ms. To reach -2dB in 5ms, the charging time constant of the RC circuit would need to be around 1.25ms. Thus, the integration time is approximately 4 tau RC circuit.
In addition to the integration time, quasi-peak meters have a return time that is much longer. This time determines how fast the reading will fall after the signal is removed. If this time is made small (for example, equal to the integration time), then the indicator readings will change too quickly, making them difficult to read. For VU meters, such a problem did not arise due to their low speed, one time constant could be dispensed with. In high-speed quasi-peak meters, it is necessary to artificially slow down the fall in readings so that the operator can read the information.
The return time determines how quickly the meter reading will fall by 20 dB after the signal is removed. It is also not equal to the discharge time constant of the RC circuit, but is approximately 2.3 tau. The return time value is also set by the standards. It differs for indicators of different purposes. For indicators of the first type, which serve to check the signal level during its operational adjustment (this is just the case of adjusting the recording level in a tape recorder), the return time should be 1.7±0.3 sec. Accordingly, the discharge time constant of the RC circuit should be approximately 740 ms.
Level meters have another dynamic characteristic - response time. It may not be entirely clear. For inertialess devices, ballistics is artificially formed, similar to pointer devices. Increasing the response time in this case should not increase the integration time of the meter. The short signal pulses should still display correctly. To do this, the detector must "wait" until the reading reaches the measured value, and only then start the fall. In amateur designs of quasi-peak meters, with a fast increase in the signal level, the bar immediately jumps from one length to another. This is not the case with professional quasi-peak meters, because the increase in response time has a positive effect on the perception of readings by the operator. In VU meters, this is also not the case, there the smoothness of movement is obtained due to the large integration time. The response time is defined as the interval from the moment the test tone burst begins until the reading reaches -1 dB.
Integration time
To obtain a given integration time, the detector output must be smoothed with a filter. The smoothing filter is not a simple low-pass filter, but a more complex filter with different charge and discharge time constants. The charge must be fast to provide the specified meter integration time. And the discharge must occur slowly to provide a given return time, which is much longer. Therefore, the integration time filter is turned on only when the signal rises; when the signal decreases, it is kept at the same level. A separate filter is used for signal decay.
The difference filter equation has the following form:
y( n ) = y(n-1) + A*(x( n ) - y(n-1)), where A = 0.0083 for Fs = 96 kHz
A 32-bit accumulator is used to obtain the required calculation accuracy. Filter coefficients are 16-bit unsigned. They are defined as A = 65536 / 96000 / tau.
Attachments
Are you really fine with IC voltage regulators ?
- By ginetto61
- Power Supplies
- 591 Replies
Attachments
PeeCeeBee V4 GB!
- By shaan
- Group Buys
- 1099 Replies
Hello guys!
A fresh new PeeCeeBee is here, the V4! In this thread group-buys for the printed circuit boards are arranged.
It's a Lateral MOSFET based Class-AB amplifier with symmetrical "current feedback", evolved from from the diverse PeeCeeBee series, and now with excellent sonics coupled with excellent looks. 🙂
The new design is electrically and sonically a step forward from the "stubbornly" simple but very good sounding designs released in the original PeeCeeBee thread. I say a step forward partly because it incorporates some extra well-known techniques to handle some of the problem areas in the old designs and allows a quicker and safer mode of set-up and operation, but mostly because while doing so it didn't become a fatigue-inducing clinical sounding amplifier. The layout is designed by myself and the amplifier is very stable, both thermally and electrically. The amplifier has similar sonic signature to the previous peeceebees in the mid and high frequency band, but the low-frequency performance has been substantially improved so that it can be used as a full-range amplifier with effortless bass as well as beautiful midrange and highs.
It uses a simple but effective diode-clamp based soft-clipping so that occasional overloads don't bother listening enjoyment. The two jumpers, when open, remove the chance of overloading Q9/Q10 while setting-up. The constant current sources keep the input/VAS bias much less affected by power supply variation during loud playback and/or mains fluctuation.
The following two screenshots show the design:
This is how the PCB looks in real world:
A fully assembled channel:
Some specs (measured with generic components/passives and basic unregulated linear PSU):
Maximum Power - 50WRMS/90WRMS into 8R/4R load with +/-35V PSU
Maximum allowed PSU voltage for 4R operation - +/-35V (with default clamp diodes and BD BJTs for Q9/Q10) and +/-42V (with higher voltage rated clamp diodes and MJE BJTs for Q9/Q10)
Frequency response(simulated) - ~2Hz to ~800KHz (-3dB)
AC gain - 23 (27dB)
DC gain - Unity
Input level for 50WRMS into 8R - 1VRMS
THD 100Hz 10W - 0.0005%, 1KHz 10W - 0.001%, 10KHz 10W - 0.002%
Slew Rate - 100V/uS
SNR - >100dB
Offset variation - +/-10mV
Screenshot of 1KHz THD spectrum (10W into 8R resistive load, 0.002% source THD):
Screenshot of 1KHz + 5.5KHz IMD spectrum (1.7W into 8R load):
__________________________________________
Group Buy Information:
The PCBs are 92mmx64mm 2-Layer and I plan to batch-print 50, 75 or 100 PCBs depending on interest and how many people join in the GB list. The boards are made with 2.4mm FR4, 60micron copper, HASL finish, white silkscreen and black solder mask, as shown in the above pictures.
> The PCBs cost US$10 a piece.
> After the GB list is full, each user will be contacted and sent the first invoice for PCB cost, and the rest (including shipping charge, packing and processing charge and PayPal charge) is to be paid before shipping the boards, for which the second invoice will be sent.
> International payments are accepted through PayPal and payments from within India are accepted through bank account transfer/deposit, NEFT etc.
> Delay between placing the batch order to PCB plant and delivery of the boards to me will be 18-20 days.
Shipping Information:
Two forms of shipping available. International Air Parcel and Registered Post. Former takes about 15-20 days to deliver and the latter takes about 30-40 days. Both support tracking.
_____________________________________________________
GB1 (April 26 2017)
--------------------------------
Update: Pending members and anyone wishing to join, Please notice:
PM/invoices will be sent up-to 5th May.
Last day of confirming order is 7th May.
PCBs will be ordered on 8th May.
Update(May 9 2017): Total 120 boards ordered. There are still 10 spare PCBs so join in if interested in a couple.
Update(May 11 2017): GB list full. No new entries are being taken until June 1 2017.
GB1 Ended.
--------------------------------
GB2 (June 15 2017)
-------------------------------
Second group buy has started.
GB2 Ended.
-------------------------------
GB3 (Sept 12 2017)
-------------------------------
Third group buy is now open for entry. Join in if interested!
GB3 Ended
-------------------------------
GB4 (Dec 23 2017)
-------------------------------
Fourth group buy has started.
GB4 Ended.
-------------------------------
GB5 (Aug 17 2018)
-------------------------------
Fifth Group Buy arranged. Boards available.
_____________________________________________________
Important Links:
Download Latest BOM for PeeCeeBee V4 >Here<
Download Setup Guide And Component Indication >Here< (Follow this to populate and start the PCBs)
Heat Sink Drill Template >Here<
Thanks.
shaan
🙂
A fresh new PeeCeeBee is here, the V4! In this thread group-buys for the printed circuit boards are arranged.
It's a Lateral MOSFET based Class-AB amplifier with symmetrical "current feedback", evolved from from the diverse PeeCeeBee series, and now with excellent sonics coupled with excellent looks. 🙂
The new design is electrically and sonically a step forward from the "stubbornly" simple but very good sounding designs released in the original PeeCeeBee thread. I say a step forward partly because it incorporates some extra well-known techniques to handle some of the problem areas in the old designs and allows a quicker and safer mode of set-up and operation, but mostly because while doing so it didn't become a fatigue-inducing clinical sounding amplifier. The layout is designed by myself and the amplifier is very stable, both thermally and electrically. The amplifier has similar sonic signature to the previous peeceebees in the mid and high frequency band, but the low-frequency performance has been substantially improved so that it can be used as a full-range amplifier with effortless bass as well as beautiful midrange and highs.
It uses a simple but effective diode-clamp based soft-clipping so that occasional overloads don't bother listening enjoyment. The two jumpers, when open, remove the chance of overloading Q9/Q10 while setting-up. The constant current sources keep the input/VAS bias much less affected by power supply variation during loud playback and/or mains fluctuation.
The following two screenshots show the design:
This is how the PCB looks in real world:
A fully assembled channel:
Some specs (measured with generic components/passives and basic unregulated linear PSU):
Maximum Power - 50WRMS/90WRMS into 8R/4R load with +/-35V PSU
Maximum allowed PSU voltage for 4R operation - +/-35V (with default clamp diodes and BD BJTs for Q9/Q10) and +/-42V (with higher voltage rated clamp diodes and MJE BJTs for Q9/Q10)
Frequency response(simulated) - ~2Hz to ~800KHz (-3dB)
AC gain - 23 (27dB)
DC gain - Unity
Input level for 50WRMS into 8R - 1VRMS
THD 100Hz 10W - 0.0005%, 1KHz 10W - 0.001%, 10KHz 10W - 0.002%
Slew Rate - 100V/uS
SNR - >100dB
Offset variation - +/-10mV
Screenshot of 1KHz THD spectrum (10W into 8R resistive load, 0.002% source THD):
__________________________________________
Group Buy Information:
The PCBs are 92mmx64mm 2-Layer and I plan to batch-print 50, 75 or 100 PCBs depending on interest and how many people join in the GB list. The boards are made with 2.4mm FR4, 60micron copper, HASL finish, white silkscreen and black solder mask, as shown in the above pictures.
> The PCBs cost US$10 a piece.
> After the GB list is full, each user will be contacted and sent the first invoice for PCB cost, and the rest (including shipping charge, packing and processing charge and PayPal charge) is to be paid before shipping the boards, for which the second invoice will be sent.
> International payments are accepted through PayPal and payments from within India are accepted through bank account transfer/deposit, NEFT etc.
> Delay between placing the batch order to PCB plant and delivery of the boards to me will be 18-20 days.
Shipping Information:
Two forms of shipping available. International Air Parcel and Registered Post. Former takes about 15-20 days to deliver and the latter takes about 30-40 days. Both support tracking.
_____________________________________________________
GB1 (April 26 2017)
--------------------------------
Update: Pending members and anyone wishing to join, Please notice:
PM/invoices will be sent up-to 5th May.
Last day of confirming order is 7th May.
PCBs will be ordered on 8th May.
Update(May 9 2017): Total 120 boards ordered. There are still 10 spare PCBs so join in if interested in a couple.
Update(May 11 2017): GB list full. No new entries are being taken until June 1 2017.
GB1 Ended.
--------------------------------
GB2 (June 15 2017)
-------------------------------
Second group buy has started.
GB2 Ended.
-------------------------------
GB3 (Sept 12 2017)
-------------------------------
Third group buy is now open for entry. Join in if interested!
GB3 Ended
-------------------------------
GB4 (Dec 23 2017)
-------------------------------
Fourth group buy has started.
GB4 Ended.
-------------------------------
GB5 (Aug 17 2018)
-------------------------------
Fifth Group Buy arranged. Boards available.
_____________________________________________________
Important Links:
Download Latest BOM for PeeCeeBee V4 >Here<
Download Setup Guide And Component Indication >Here< (Follow this to populate and start the PCBs)
Heat Sink Drill Template >Here<
Thanks.
shaan
🙂
Attachments
For Sale FS Scak Speak Sonus Faber Cremona units in KIT
UPDATED SALE.
Here for sale some Sonus Faber Cremona units.
Some units came from my Cremonas (damaged when my son pushed the dust cap of a woofer with his finger). A pair of woofers came from SF SAT. I will explain:
2x SF Cremona Tweeters. Perfect condition. No damages. They are used and in perfect working and cosmetic condition.
Asking 100€ +pp fees + shipping for the pair
2x SF Cremona Scan Speak 18W8531/G03 Woofers from my Original Cremonas.
One was repaired because the dust cap was damaged by my son. Speakers leads changed as well. Everything was repaired in a Professional service. I can provide invoice.
They measure the same. Perfect working condition. Some minor cosmetic issues (7/10).
Asking 190€ +pp fees + shipping for the pair
2x SF Cremona Scan Speak 18W8531/G03 Woofers
This pair of woofers came from one friend from SF SAT.
The owner coated them. They measure the same than original ones.
Perfect working condition. Average looking condition due to coating (5/10)
Asking 160€ +pp fees + shipping for the pair
I can make lots at discounted price and I can include for free a pair of front baffle for woofers
Each (mm) 758H x 210W x 19D Capable for 2x Scan Speak 18W8531 woofers and a jantzen Ø100mm Bass Refflex port (Ø138,50mm hole)
Here for sale some Sonus Faber Cremona units.
Some units came from my Cremonas (damaged when my son pushed the dust cap of a woofer with his finger). A pair of woofers came from SF SAT. I will explain:
2x SF Cremona Tweeters. Perfect condition. No damages. They are used and in perfect working and cosmetic condition.
Asking 100€ +pp fees + shipping for the pair
2x SF Cremona Scan Speak 18W8531/G03 Woofers from my Original Cremonas.
One was repaired because the dust cap was damaged by my son. Speakers leads changed as well. Everything was repaired in a Professional service. I can provide invoice.
They measure the same. Perfect working condition. Some minor cosmetic issues (7/10).
Asking 190€ +pp fees + shipping for the pair
2x SF Cremona Scan Speak 18W8531/G03 Woofers
This pair of woofers came from one friend from SF SAT.
The owner coated them. They measure the same than original ones.
Perfect working condition. Average looking condition due to coating (5/10)
Asking 160€ +pp fees + shipping for the pair
I can make lots at discounted price and I can include for free a pair of front baffle for woofers
Each (mm) 758H x 210W x 19D Capable for 2x Scan Speak 18W8531 woofers and a jantzen Ø100mm Bass Refflex port (Ø138,50mm hole)
TDA1541A DAC Project Discussion
- Digital Line Level
- 7 Replies
Hi,
I am sharing the file I got from my friend, it's a TDA1541A DAC with multiple input interface including I2S.
Also, for convenience there is a InterActive BOM that helps a lot while soldering components.
The attached .Zip file contains
A) GERBER files in Zip, ready for fabrication.
B) BOM in HTML.
Please let me know if there is problems.
Regards,
J
I am sharing the file I got from my friend, it's a TDA1541A DAC with multiple input interface including I2S.
Also, for convenience there is a InterActive BOM that helps a lot while soldering components.
The attached .Zip file contains
A) GERBER files in Zip, ready for fabrication.
B) BOM in HTML.
Please let me know if there is problems.
Regards,
J
Sonos/IKEA Symfonisk hack
- By Sigrm
- Construction Tips
- 5 Replies
Hi there,
I read this article about hacking the Sonos / IKEA Symfonisk, and thought I'd try it with a nice old radio I have in my kitchen. It earns its keep as a decoration alone, but it sure would be nice to get it playing as well.
Now, the first issue that I've run in to (I'm sure there will be more), is that the radio only has one single woofer, while the Sonos looks like some sort of bi-amp setup. I'm not familiar with such. Would it be possible to wire both sets of cables to the same woofer?
From makezine.com:
I read this article about hacking the Sonos / IKEA Symfonisk, and thought I'd try it with a nice old radio I have in my kitchen. It earns its keep as a decoration alone, but it sure would be nice to get it playing as well.
Now, the first issue that I've run in to (I'm sure there will be more), is that the radio only has one single woofer, while the Sonos looks like some sort of bi-amp setup. I'm not familiar with such. Would it be possible to wire both sets of cables to the same woofer?
From makezine.com:
Project Madness
Hello all
Everyone who know me understand that I am a big Audio Physic fan, so when I see this one launched at hi end München show, I am getting really stunned... at every point. There are many things that tick boxes here
https://www.audiophysic.com/en/medeos/
This is a really complex thing to do, 5 way with 3 separate cabinets each side.... Call me absolutely insanely crazy but I am thinking, is this a project I would like to consider?, maybe 😱
It could be a setup with Bliesma beryllium tweeters and hi mids, Purify mids and woofers, several possibilities with subwoofers. But to have any chance it must be active with digital crossovers, this would easily be a €20K to €30K project, so there is pretty high risk here.... I have a working title of "project madness" 🤣
I have not been doing any simulations or calculations on cabinets sizes and/or setup yet.....
Any thoughts guys
Login to view embedded media
Everyone who know me understand that I am a big Audio Physic fan, so when I see this one launched at hi end München show, I am getting really stunned... at every point. There are many things that tick boxes here
https://www.audiophysic.com/en/medeos/
- Point source, or really close to point source, the whole passband down to around 300 Hz is managed by the central 3 drivers really close together, the other drivers symmetrically around this point.
- Lot of cone area in the mid-bass up to 300 Hz, must leave us with unreal dynamics, and there is nothing like lots of cone area
- Woofers for midbass located low and high which means it triggers different room modes and so should be more even mid-bass and less room influence with mid-bass, the same gows for the lower bass
- Integrated subwoofers, an all in one solution that makes it feasible to place even in a medium size flat (like mine)
With four large / tall towers my place would look like Stonehenge, I don´t want that.... this is also going into the main living room - Really really really cool design, the way it looks, IMHO 😍
This is a really complex thing to do, 5 way with 3 separate cabinets each side.... Call me absolutely insanely crazy but I am thinking, is this a project I would like to consider?, maybe 😱
It could be a setup with Bliesma beryllium tweeters and hi mids, Purify mids and woofers, several possibilities with subwoofers. But to have any chance it must be active with digital crossovers, this would easily be a €20K to €30K project, so there is pretty high risk here.... I have a working title of "project madness" 🤣
- Bliesma T34B beryllium tweeter
- Bliesma M74-B beryllium upper midrange
- Purify 5.25" midrange down to 300 Hz
- 4 * Purify 6.5" Midbass 100 til 300 Hz
- 8 * Purify 8" sub-bass or many other choices from Seas, Peerless, ScanSpeak, SB Acoustics....
- Marani LPP480A FIR Speaker management system (only supports up to 2 x 4 channels though)
I have not been doing any simulations or calculations on cabinets sizes and/or setup yet.....
Any thoughts guys
Login to view embedded media
Passive crossover 2 way - 4 inductors ideal layout, please advise
Hello all,
here is my DCX464 crossover layout - it contains 4 coils. The bottom part is low pass for the mid part (LCL) and the upper part has a highpass (LC) on the left and a notch filter inductor on the right. The board is now 240 x 240 mm. The C-C distance of the inductors as shown is 170 mm along the edges. The squares are other components and terminals. Can I get the board smaller by rotating the inductors better? I could follow the orientation rules for two or three, but what would be the preference when having 4 with these functions? I think I can leave the boards this large, maybe shift the smaller inductors further away a bit closer to the edges if there is nothing much to be gained from different orientation of the inductors. Any opinion is welcome.
here is my DCX464 crossover layout - it contains 4 coils. The bottom part is low pass for the mid part (LCL) and the upper part has a highpass (LC) on the left and a notch filter inductor on the right. The board is now 240 x 240 mm. The C-C distance of the inductors as shown is 170 mm along the edges. The squares are other components and terminals. Can I get the board smaller by rotating the inductors better? I could follow the orientation rules for two or three, but what would be the preference when having 4 with these functions? I think I can leave the boards this large, maybe shift the smaller inductors further away a bit closer to the edges if there is nothing much to be gained from different orientation of the inductors. Any opinion is welcome.
House numbered TI transistor
Does anyone have a clue as to the specs or what his transistor cross references to? Not an audio transistor but from an IBM 3278 terminal. It's shorted and no schematics are available. Thanks.
(2) Focal woofers 7K011 DBL 7" speakers vintage pair dual voice coil 7 inch -- NH USA --
Attachments
-
20220728_093844.jpg -
20220728_093847.jpg -
20220728_093850.jpg -
20220728_093854.jpg -
20220728_093955.jpg -
20220728_094000.jpg -
20220728_094026.jpg -
20220728_094028.jpg -
20220728_094031.jpg -
20220728_094033.jpg -
20220728_094036.jpg -
20220728_094115.jpg -
20220728_094122.jpg -
20220728_094133.jpg -
20220728_094135.jpg -
20220728_094151.jpg -
20220728_094201.jpg -
20220728_094208.jpg
For Sale TO-3 SymAsym boards
- By Groundloops
- Swap Meet
- 8 Replies
For sale 3 pairs of Rudi Ratlos TO-3 SymAsym boards. Asking €25,00 per pair + postage. Shipping from Germany.
Sub tuned incorrectly?
- By Daan32
- Subwoofers
- 11 Replies
- TLDR: Subs tuned wrong? Sound kind of boomy and you don't feel the bass quite as much as expected, as there are 4x 18 Inch woofers (4 sub boxes in total, 1 woofer per box). Default tuning frequency is 50Hz, I calculated it for 35Hz and added some ports for that frequency, but that sounds a lot less loud. I'm wondering what the best solution would be for feeling the bass and sounding the best. Subs are hooked up in 2x2 parallel, that makes 4 Ohms. They're hooked up to QSC Powerlight 4.0's (not bridged)
Hi All!
So first of all, I'm quite new to this so I'll most definitely be making some mistakes 😅
Now onto my question,
I have 4 subwoofer cabinets which (I think) are tuned incorrectly. I'm thinking this because they sound very, boomy? And you don't really feel the bass quite as much as I would be expecting, especially since there are 4 18 inch woofers. They're hooked up in 2x2 parallel, which makes 4 ohms, to some QSC Powerlight 4.0's (not bridged)
Specs of the cabinets:
I've attached picture of them for a bit more clarification. Right port has the port calculated for 35Hz and the left port is how they are right now, tuned to 50Hz (just for example)
Woofer: B&C 18pzb46 (https://www.bcspeakers.com/media/W1siZiIsIjIwMTMvMDMvMTEvMTUvNTIvMzAvNTQyL2ZpbGUiXV0)
Volume (internal): 185L (calculated BEFORE the woofer was inserted, don't know if that's correct?)
outer dimensions: 64x52x72cm
ports: 2; slotted; depth 2.8cm ;9x12cm; rounded eges; surface area = 90.6cm2, same as 10.74cm diam. Circle
Now I've been playing around with these specs on some calculator websites to try and tune these subwoofer boxes
Tuning frequency calculation:
First I calculated the tuning frequency, which I thought was necessary, using this website:
https://www.vcalc.com/wiki/subwoofer-tuning-frequency
Values I used:
Air compliance: 155L (Vas in woofer datasheet, is that correct value to use?)
Enclosure volume: 185L
Speaker resonant frequency: 37Hz
These values returned a tuning frequency of ~35Hz
Port length calculation:
I then entered these values in the following website:
http://www.mh-audio.nl/Calculators/WVC.html
I used the top most calculator to calculate the porth lenght.
values I used are:
Dv: 10.24cm (i'm going to 3D print the port, which means that the port will be a little smaller because of the 3D prints wall)
Np: 2
Vb: 185L
fb: 35Hz
k: 0.732
this resulted in a porth lengt of 14.31cm, I 3D printed this, installed it into the subwoofer and sure enough, It sounds quite a lot better on the low end!
But then I noticed that around 50Hz, the sub is quite a lot less loud.
WinISD:
So I went looking for speaker response curve programms, and found one called WinISD. I entered the subs paramaters here and tuned it to 50Hz, 40Hz (in between 50Hz and 35) and 35Hz
The 50 Hz is how it's tuned withouth any additional port, since the front wood is 2.8cm thick.
These are the 3 waveforms in WinISD
Red = 50Hz
Green = 40Hz
Blue = 35Hz
The 50Hz has a way higher peak than the other 2 waveforms, which explains why it's such a lot louder at 50Hz, but under 45 Hz it sounds just terrible.
Best advice?
What would your advice be? I'd like to feel the bass as I said, and also for it not to be boomy. Tune it to 40Hz so It's the best of both worlds? Or tune it to 35Hz and would that be loud enough? Or don't tune them at all so they're at 50Hz and just have a really steep high pass filter at around 35-40Hz, so those bad sounding and power consuming low frequencies are cut off, which also would make it so that the amp has a bit more power to spare?
I'd like to hear from you!
Thanks in advance,
-Daan
Attachments
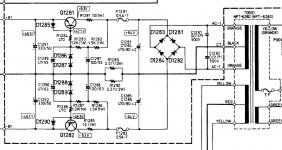
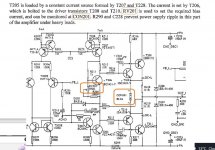
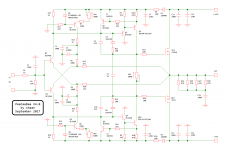
![20221004_202719[1].jpg](/community/data/attachments/1004/1004624-0886de6054d37a64c8898d713a69e716.jpg?hash=CIbeYFTTem)
![20221004_202726[1].jpg](/community/data/attachments/1004/1004625-417254cee2a93271fee56cadcd6d1253.jpg?hash=QXJUzuKpMn)
![20221004_202736[1].jpg](/community/data/attachments/1004/1004626-0f9204467af49f944573b519edba62d2.jpg?hash=D5IERnr0n5)
![20221004_210122[1].jpg](/community/data/attachments/1004/1004627-572fcfce1d07907feabaa8a3e4a66d26.jpg?hash=Vy_Pzh0HkH)
Genuine or Fake parts
- By Shelah
- Solid State
- 25 Replies
Goodday All
i recently purchased 2sc5200 and 2sa1943 from a local supplier. i have some doubts on the authenticity of them given that the TTC and TTA versions are a better version of these parts. With the uploaded images, can we say these are genuine or fake parts? i need assistance because i have a class h amp where i need to use them on.
please note that the physical dimensions and weight of these are the same with the ttc and tta trannys i already have.
Thanks in advance.
i recently purchased 2sc5200 and 2sa1943 from a local supplier. i have some doubts on the authenticity of them given that the TTC and TTA versions are a better version of these parts. With the uploaded images, can we say these are genuine or fake parts? i need assistance because i have a class h amp where i need to use them on.
please note that the physical dimensions and weight of these are the same with the ttc and tta trannys i already have.
Thanks in advance.
Attachments
trying to understand relationship of Vsupply to Vout (graph and datasheet link inside)
- By mrjayviper
- Parts
- 14 Replies
maybe it's best explain with an example:
This is my circuit:
The way I read the graph is that if I require Iout=2amps then difference between Vsupply and Vout must be at around 3V. (though I'm unsure what Vsupply means in the case since it's a +/- supply)
Here's the graph (There's a high chance I'm looking at the wrong graph but I cannot find anything else suitable in the datasheet)
Here's the full datasheet: https://www.ti.com/lit/ds/symlink/opa548.pdf
This is my circuit:
- Vin is connected to a 5V reference (via a zener diode or a chip like a REF02)
- Vsupply is +/- 16-18V (controlled via an LM317 or equivalent chip so it can be anything within the LM317 limits)
- Vout is calculated at around 12V (Rf=24Kohms | Rin=10Kohms ) (5V * 24/10 = 12V)
The way I read the graph is that if I require Iout=2amps then difference between Vsupply and Vout must be at around 3V. (though I'm unsure what Vsupply means in the case since it's a +/- supply)
Here's the graph (There's a high chance I'm looking at the wrong graph but I cannot find anything else suitable in the datasheet)
Here's the full datasheet: https://www.ti.com/lit/ds/symlink/opa548.pdf
-
Poll
JBL Control SB5 modifications
- By dannyjmf
- Subwoofers
- 5 Replies
Recently having bought home a used JBL control SB5 subwoofer ... after 1 day use and getting hand itchy decided to Mod it by swapping in china made "JBL" knock off woofers into the original enclosure .... after modifications as shown below ... bass performance is about the same as the original except the original has slightly higher power handling ... i want to hear opinions from members in this forum should i use this subwoofer in the Modded form or put everything back to the original (the original drivers were removed and well kept in storage box) .... originally it has 4 drivers which could be difficult load for amplifiers but now after mod only using 2 drivers ... thanks
Attachments
Audera sub-woofer amplifier, used, amplifier only
Used Audera HD800 0.1 Class D amplifier. Supposedly 650W at 0.1%. "LFE" (no filter) RCA input on small interface board with volume control, power indicator. "Usable" response 10Hz out to 1kHz. Tested, operational. No power supply, only what's pictured. Power input connector clearly designated.
Originally, this amplifier sends a signal to a switching power supply such that it varies its +/- rails in response to the input amplitude. I connected it to a +/- 30VDC, 60 Hz iron transformer based PSU (ignoring the control wire) and it played. I'll guess the max PSU voltage for this amp is +/- 40V, based in its claimed bridged output max p-p voltage of "160V p-p".
I'll assume one could make a powered sub using this, or a bass guitar amplifier - with lots of headroom - by adding an appropriate power supply. I neither need a 650W sub, nor a 650W bass amp...
I'd like $40 for it, plus shipping - USA / Canada only unless you can convince me otherwise. Thanks,
Originally, this amplifier sends a signal to a switching power supply such that it varies its +/- rails in response to the input amplitude. I connected it to a +/- 30VDC, 60 Hz iron transformer based PSU (ignoring the control wire) and it played. I'll guess the max PSU voltage for this amp is +/- 40V, based in its claimed bridged output max p-p voltage of "160V p-p".
I'll assume one could make a powered sub using this, or a bass guitar amplifier - with lots of headroom - by adding an appropriate power supply. I neither need a 650W sub, nor a 650W bass amp...
I'd like $40 for it, plus shipping - USA / Canada only unless you can convince me otherwise. Thanks,
FREE Marantz equipment for pick up
Available for pick up in Napa, CA:
Marantz Model 1030 integrated amp
Marantz Model 2216 Receiver
Both pieces are in working condition. However controls are scratchy and need either DeOxit or replacement.
Sorry, I'm not shipping these. If you can pick them up in Napa you are 1 lucky DIYer!
Marantz Model 1030 integrated amp
Marantz Model 2216 Receiver
Both pieces are in working condition. However controls are scratchy and need either DeOxit or replacement.
Sorry, I'm not shipping these. If you can pick them up in Napa you are 1 lucky DIYer!
Can anyone identify this voltage sticker
- By stoolpigeon
- Everything Else
- 3 Replies
Evening all, have been sorting out a lot of electronics and found this sticker on the floor.
AFAIK all these components are 230-240 volts so does anyone recognise this sticker so I can investigate?
Thanks, sp
AFAIK all these components are 230-240 volts so does anyone recognise this sticker so I can investigate?
Thanks, sp