Yes, that Marius Tanasescu repeats the same things you can find written in this forum. Not that a lie repeated thru and thru becomes the truth ...🙄
I'm still not convinced that SW might happen inside speaker enclosures
Well, you can easily measure them with a measuring microphone, sound card and some cheap software. Just take an enclosure with and without damping material, and do a FR measurement, close miked. The differences are caused by standing waves.
But please tell me, why do you think there are no standing waves inside an enclosure? You must have done some thinking on this and I am curious to find out what it is.
But please tell me, why do you think there are no standing waves inside an enclosure? You must have done some thinking on this and I am curious to find out what it is.
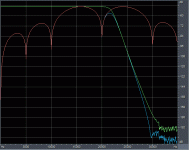
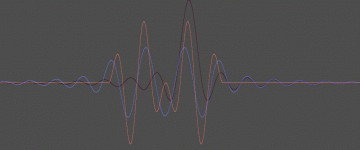
Here we go (well, actually sin(20)*sin(5), but we won't be nitpicking here). As expected, it looks exactly the same conceptually. Pulse center widened to reflect the now more dominant lower frequency, and pulse tails approaching natural ripple frequency of the filter.
In the spectrum we can see the bulk frequency content is in the 15k and 25k regions, as suggested by trig identities. The filter affects the 25k "hill" only.
EDIT: the high points are *not* at 15k and 25k exactly, more like ~16k and ~24k (not related to the 20x4 thing), the reason being the underlying bell-shaped EQ on the leafes of the spectrum.
This shows that the high points in the spectrum of a blip (not a peridic AM of two infinite sines -- with whatever phase angle, which affect only details of time display) are not a good measure of "where the frequencies are", nor is zero-crossing distances. Both loose their meaning to indicate "frequency" when used with non-infinite sines (single, sums or products) or when EQ is applied (no matter if explicitely or intrinsic to the process).
Attachments
Last edited:
The potentil trouble is it will sound different, becase you will be able to fear the upper sideband, so may hear it's loss, whereas with the 20 and 4k the upper sideband is definitely inaudible.
My next job - overlay Hans' wav file to look for the effect you suggested...
Yes, but.....as elektroj says it will change the "signature" not the pitch, have you listened to his modified files, what do you think?
Nice work, last sentence, well...
I note you ran the full sine instead of one lobe, great. Now run 20 or 30 cycles and look at the output, your blue waveform. Run it for minutes, days if you want. How long does a sine signal have to run to "qualify" as having a frequency?
I'm not being snarky, just curious where a constant frequency wave of any shape graduates to having frequency, as one lobe "clearly" does not qualify.
Also note, your output no longer has the amplitude modulation of the input. That is the crux of this sideband discussion. The more upper sideband removed, the flatter the envelope and the closer to the lower frequency the output gets.
Ps.. I also assume that with 20 or 30 cycles, your spectra will tighten up due to sample size.
Jn
Last edited:
I can hear 15k day and night, trivially easy.
And I mean day and night. A constant high pitch in my ears, never goes away..
Richard, could you do us a favor? If you have the reference source information for data you post, would you attribute? Sometimes I want to follow up but don't know where to look.
Thanks,
Jn
Let's be careful with simplification a bit lest it be misunderstood by others. I said 20k modulated, as a steady state sine will never be frequency shifted by a filter.
As I earlier mentioned, the sum of two sines is a lobed structure with the average of the frequencies as the lobe content. That average frequency is the result of one frequency phase walking the other. If you change the amplitude ratio of the sines, the internal lobe frequency will head towards the dominant frequency and the envelope smooths out more. So the final result will depend on how much of the USB is actually removed. And the average within lobe frequency flips phase every lobe, so does not show up on an FFT. However, as the ratio of the sine amplitude changes, the inner lobe frequency will start to show up on the FFT.
Using raised sine modulation (which never occurs in natural music IMHO), the carrier will influence the time domain picture. Removal of the USB in that case leaves carrier and LSB, and the output will look like modulation around the average of LSB and carrier and at half the modulation rate.
As KSTR is heading towards, supressed carrier modulation (the trig identity is two sines added), when the USB is removed. All that is left is the lower USB.
Jn
Last edited:
I got a kick outta this episode at work..
One experiment is long baseline X-ray nano probe. A diffraction grating/mirror combo selects the wavelength desired, focuses the beam 100 meters away, with spot size in the low nanometer range.
One day, the scientist noticed that the beam spot was moving vertically at a 1 Hz rate. Huge effort was spent tracking down a 1hz ground vibration. Geophones all over the place.
Nothing. Just a spike at 29.5 Hz. Modulating, of course...
We use two types of vacuum pumps, one line locked in freq, one VSD. The VSD was rotating below line frequency....just below, 59 Hz.
So I asked the researcher, what is his video camera refresh rate?
He asked...why?😕
Armed with a better understanding, we found a clamp around a bellows which transferred the vibe of the pumps. Removed it, gtg.
Jn
Ps.. Apparently, the mechanical pumps vibrate the ground at half line frequency. Not sure why, but it's in the Manu literature.
Pps..previous post I said "lower USB"... Duh, meant lower sideband, or LSB..
One experiment is long baseline X-ray nano probe. A diffraction grating/mirror combo selects the wavelength desired, focuses the beam 100 meters away, with spot size in the low nanometer range.
One day, the scientist noticed that the beam spot was moving vertically at a 1 Hz rate. Huge effort was spent tracking down a 1hz ground vibration. Geophones all over the place.
Nothing. Just a spike at 29.5 Hz. Modulating, of course...
We use two types of vacuum pumps, one line locked in freq, one VSD. The VSD was rotating below line frequency....just below, 59 Hz.
So I asked the researcher, what is his video camera refresh rate?
He asked...why?😕
Armed with a better understanding, we found a clamp around a bellows which transferred the vibe of the pumps. Removed it, gtg.
Jn
Ps.. Apparently, the mechanical pumps vibrate the ground at half line frequency. Not sure why, but it's in the Manu literature.
Pps..previous post I said "lower USB"... Duh, meant lower sideband, or LSB..
Last edited:
That seems a sensible assumption but probably not for the reason you suggest, maybe Mark will be able to enlighten us?
The suggestion was, that when removing an upper sideband above 20Khz with a BriWa filter, that the harmonics below 20Khz that came with this HF sideband become shifted in frequency.
The other way round, a lower sideband below 20Khz should be altered when removing its HF brothers above 20Khz.
This idea originated, because when looking at the time domain signal a frequency shift seemed to occur after BriWa filtering @20Khz.
In the frequency domain however, no such thing was ever visible, and every frequency below the BrWa keeps its place spot on.
Two things are happening to the time domain signal while filtering, 1) HF content is removed and 2) Depending on the signature of the HF content, a signal is added in the form of Gibbs ringing at 20KHz.
Therefore, there is no magic involved that the shape of the time domain looks different after filtering, since the original signal it is now the sum of 3 signals, (original - HF + Gibbs).
And exactly because it is not just one signal but the sum of 3, it's impossible to derive one single frequency from it and conclude that a frequency shift has taken place.
When two different filters are used, like Elektroj did in #330, different Gibbs patterns are generated, leading to completely different time domain signals.
But in all those cases, the FFT will tell that below the BrWa everything is still untouched.
I can only repeat my opinion that we listen to frequencies and not to time domain envelopes.
So after all attemps to explain that the above thesis is wrong, maybe the scaling down effort in #329 might confirm that no frequency shift takes place.
And when it does confirm an absence of frequency shifting and everybody accepts it, then we are finally done with it and so is the theory rejected that 44.1K cripples the sound of a 96K or 192K recording.
Hans
Last edited:
Its basic data, all over the place via Google. Not at all hard to find. Just pasted there to say what i said.
🙂
But, I will try better.
-Richard
No. There are several issues which affect the sound.
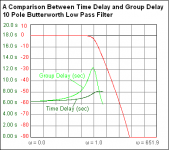
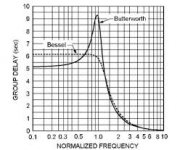
Anyway, I have a question... which of the filters being used here has flat GD to 22Khz?
[The advantage of IIR filters over FIR filters is that IIR filters usually require fewer coefficients to execute similar filtering operations, that IIR filters work faster, and require less memory space. ... FIR filters are better suited for applications that require a linear phase response.]
THx-RNMarsh
Attachments
Last edited:
No, that is incorrect.
Using a proper modulation, sin(hf)cos(lf) the FFT will not see the hf, but only the sidebands. This is due to 200%modulation, the hf phase inverts every lobe.
The math says the lobe frequency is there. I suspect your argument is with a gentleman who is dead more than a thousand years.
Believing it doesn't exist because an FFT cannot see it...hmmm
I suspect you are overly reliant on the FFT without consideration of it's limitations.
Your use of a raised cosine (or raised sine) modulation was unfortunate, as the carrier never flips phase, never exceeds 100% modulation, so confounds the time domain discussion..and makes you come to an incorrect conclusion because the carrier is there.
OTOH, kstr's results will be more on point for audio.
Jn
Last edited:
The books by analog oscilloscope guys @ Tek and HP include very deep analysis of group delay and zeta. (The difference between Butterworth and Bessell is merely zeta; Butterworth has 0.707 while Bessell has 0.866). Look for "Wideband Amplifiers" in the title.
Words, words just endless words.
I'm curiously looking forward for you to come finally come with a prove.
Hans
Proof of what, audibility? 😉 John has stated numerous times he's not particularly interested in that.....so.....................................................