2.5 m should be enough given the smaller drivers compared to TC9. But distance measurements will reveal the true picture.
Another thing to consider might be room treatment. What you hear is a combination of speaker directivity and room absorption. Room absoprtion and FIR auto-correction can help in this regard.
Another thing to consider might be room treatment. What you hear is a combination of speaker directivity and room absorption. Room absoprtion and FIR auto-correction can help in this regard.
The Scan-Speak 602010 has been on my radar for a while, small, low resonance.
Isn't there a cheaper version that could be used in such an array?
Isn't there a cheaper version that could be used in such an array?
You're going to laugh... http://www.ebay.com/itm/Vantec-USB-...482097?hash=item4197aba271:g:3-MAAOSw~OdVdw0K
What do you mean exactly? Right now there is no treatment. Bare walls.
May add some QRD's (wood diffusors) to the front and side walls at ear height. AFAIK, absorption can do as much harm as good because it will skew the frequency response of the reflected sound. (with the acceptable 2" thick absorbers)
Any room treatment - or lack thereof - in the horizontal plane would have the same effects on the line array as on the single tweeter though, so this doesn't really explain away the treble problems from the 2" line.
Measurements don't tell the whole picture when it comes to comb filtering. Your brain is very good at parsing out high frequency "hash" if it is related to the precedence effect, and the reflections or delayed sounds are spectrally similar to the original sound.
I wasn't arguing that there is *no difference in sound* between a single driver and the line array, but rather that the treble problem did not likely originate with the sound quality of the single driver. I have to do a bit more testing of the single drivers to confirm this though...
Why would too close not work? Not really getting this from the theory - does the combing really have anything to do with angular separation in psychoacoustic terms? Isn't it simply related to the wavelengths vs. spacing?
The balance that you hear at the listening position is a combination of direct sound (speaker to ear) and total reflected sound over some time period. It has been shown many times that flat power, i.e., the measured sound at the LP (ungated), sounds bright. You want a falling power response like the B&K curve (figure 5: http://www.bksv.com/doc/17-197.pdf) at the listening position. Note that we are talking about the total response, not gated response, not anechoic response.
When you are EQing the HF response, what you want ideally is flat anechoic response or flat direct sound and falling power response. Coincidentally, this is what you get with most cone/dome systems and is caused by two factors. As frequency rises, directivity of the tweeter increases. Combine the increased directivity with higher room absorption in the high frequencies, you get a naturally falling power response. Now with your line arrays, the situation could be different. There is a lot more HF energy going into the room. This is why it is not easy to strike a balance. You want the direct sound to be flat, but the power to be falling at some rate. The B&K curve is a good target. But this may not be straight forward to achieve using conventional EQ. And this is why I'm suggesting absorption to absorb some HF energy and then combine it with DRC's auto-EQ.
Regarding absorption doing harm, I think those claims are exaggerated especially for reflections from the sides. Besides, you can put up 4" thick fiberglass or denim insulation panels on the wall, that should work down to 300-400 Hz... good enough.
No, it's not related to spacing alone. The inter-unit distance becomes less significant as you move away from the array. The phase-shift becomes smaller as you move farther away from the array. Think about it. If you are one inch away from the array, the angle subtended from the measuring point towards the centers of two drivers would be much larger than if you were 8 ft away from the array. Therefore, comb filtering moves lower in frequency as you go closer to the array. It is the same way with conventional crossovers between two drivers.
Last edited:
I will laugh all the way to the bank if it works and sound good. How does it sound? So it looks like the outputs are 3.5mm jacks and some are stereo? Were you able to access the channels independently in your Linux software and does it use ASIO drivers?
Thanks
It works OK. 16 bit / 48kHz only. There appears 8 outputs in Linux, and same on ASIO4ALL. First two channels are output SP/DIF. Also SP/DIF input.
The individual driver size doesn't actually matter much at all for vertical dispersion. It only limits horizontal dispersion and even then the taller the array becomes the less the individual driver size matters.
What matters most is the total height of the array and the listening distance. Without implementing some kind of power tapering of the outer drivers you will always get horrible combing effects as shown by Juhazi's Edge simulation.
even better is to delay the outer drivers or have a curved baffle. http://www.xlrtechs.com/dbkeele.com/images/Card Back Large.png
Last edited:
That is not true. No matter how tall an array of 8" drivers, there will be comb filtering in the HF at short listening distances. Interunit spacing is important, as is listening distance.
Imagine your measuring point is along the vertical axis of the array, i.e., you measuring from the top or the bottom of the array. At a measuring distance of 1 wavelength (at a particular frequency) away from the array, you will get perfect summing. At 1.5 wavelengths, you will get perfect cancellation, as the second unit is 180 degrees out of phase with the first, and so on. Clearly, this is the worst position to measure because interunit spacing as seen from the measurement point is the largest. Measuring from the front of the array, like we usually do, the interunit spacing becomes smaller and smaller the farther you move away from the array. In my measurements, I found it moves up one octave for every doubling of distance:
http://www.diyaudio.com/forums/mult...line-array-using-vifa-tc9-13.html#post4584879
But interunit does seem to dictate the frequency at which comb filtering will begin at a given distance.
Also, the floor-to-ceiling arrays shouldn't need power tapering and delay. It is the shorter arrays, the less than ideal arrays, that need these tricks to expand the bandwidth within which the vertical dispersion is uniform. Again, this is borne out in the measurements linked above.
Imagine your measuring point is along the vertical axis of the array, i.e., you measuring from the top or the bottom of the array. At a measuring distance of 1 wavelength (at a particular frequency) away from the array, you will get perfect summing. At 1.5 wavelengths, you will get perfect cancellation, as the second unit is 180 degrees out of phase with the first, and so on. Clearly, this is the worst position to measure because interunit spacing as seen from the measurement point is the largest. Measuring from the front of the array, like we usually do, the interunit spacing becomes smaller and smaller the farther you move away from the array. In my measurements, I found it moves up one octave for every doubling of distance:
http://www.diyaudio.com/forums/mult...line-array-using-vifa-tc9-13.html#post4584879
But interunit does seem to dictate the frequency at which comb filtering will begin at a given distance.
Also, the floor-to-ceiling arrays shouldn't need power tapering and delay. It is the shorter arrays, the less than ideal arrays, that need these tricks to expand the bandwidth within which the vertical dispersion is uniform. Again, this is borne out in the measurements linked above.
For simplicity sake, think of the array as one big tall driver cone because they are all moving together in-phase. Assume there is no gap between each driver, it's just one big radiating area. The size of each individual driver no longer matters. If you have ten 2" drivers, then putting them in array you effective now have one 2x20" quasi-rectangular driver. If you had 8" drivers then it would be like having a quasi-rectangular driver with a cone 8" wide and some multiple of 8 inches tall.
Don't forget that you don't need an array to get combing effects - a single driver can comb just that same as the sound from one part of the cone cancels with the sound from another part of the cone which is a different distance from the listener.
The combing that occurs simply becomes a function of the entire array length and the listening distance - it wouldn't matter if you had fewer 8" drivers or lots of 2" drivers, the amount of combing experienced at certain distances would be very similar. The width affects combing horizontally off axis and the height affects vertically off axis. Since you can never be vertically on axis with every driver in a very tall array until you are infinitely far away from it, you will get combing even if you a listening at the mid-point of the array.
Obviously the more speakers and/or the taller the array, the more all the peaks and dips of the combing between every combination of drivers will stagger and sum together so the combs become smaller in amplitude but there becomes more combs in the response.
Nevertheless comb filtering is still an issue for floor to ceiling arrays, just less severe than for a smaller array. For that reason, if you are going to build an array without power tapering or delay tapering it's in your best interests to build it as large as possible.
Even if you have infinite number of drivers and an infinitely tall array you still get high-shelf of -3dB beginning at a frequency dependant on the listening position because as a rule of thumb, summing of two equal amplitude incoherent (arbitrary phase) sources is +3dB and summing of two equal amplitude coherent (in-phase) sources is +6dB. At low frequency (or listening at a far distance) all the drivers are all more or less in phase so you get +6dB. As you move too close and/or the frequency becomes too high the phase of each driver at the listening position becomes chaotic so the frequency response trends towards the +3dB summing instead.
Last edited:
Sorry for the terse reply before... To elaborate, the 3dB/octave downward frequency response slope is inherent to line arrays (at all frequencies), but does not relate to the (quite high) frequency related to the center-center wavelength; the 3dB slope is present throughout.
From Jim Griffins line NFLAWP:
Far field... Spacing less than one wavelength creates a constant phase front but comb lines start to form beyond one wavelength separation. At two wavelengths separation
the first cancellation occurs. Directivity continues to decrease with more severe comb line effects as the spacing increases beyond two wavelengths.
Near field. Urban, et al [1] derives a more restrictive criterion of no more than a
half wavelength separation...
I should have pointed out before, TMM, that I get some of your points but not sure about all of it... fully agree with quote below, which I believe is what causes the downward slope in general from line arrays:
TMM said:
I just can't see how distance to the array (within reason) would cause HF dropoff. I will absolutely measure when I get home.
Thanks for the advice, there's a lot to think about. The difficulty with learning empirically about line arrays is they take so damn long to build (and so many parts!)
Why would the physical center-to-center spacing matter for an array with a large number of drivers?
Combing due to the center-to-center distance in a smaller speaker (e.g. a conventional 2 or 3 way with 2-3 drivers) is exactly the same mechanism as combing in a large array.
The reason the distance from one driver to the adjacent one in a large array no longer becomes important is because combing between drivers which are much further apart completely dominates at the listening position. i.e. if you have 20 drivers in a vertical array, the combing between two adjacent drivers around the center of the array is going to be insignificant compared to the combing created between the drivers in the center and the ends of the array.
Effectively the dominant CTC distance at the listening position becomes somewhere about half the length of the entire array.
Because the phase relationship at the listening position is going to be chaotic between all the drivers at HF. The phase between every driver is going to be somewhere between 0deg (in phase) and 180deg (cancelling) because the drivers at the ends of the array are physically further away from your ears, giving you an average of 90deg of phase. 90deg out of phase between two noise sources sum to +3dB, where as in-phase sums to +6dB. Thus you get in-phase summing at low freq and 90deg out of phase summing at HF causing a 3dB shelf (not 3dB/oct, it doesn't get any worse than -3dB) in the HF response. Note that unless you have a huge number of drivers you will still experience peaks and nulls (i.e. combing), but smoothed out you will observe an average 3dB drop in level.
With time alignment (curved baffle or DSP) to get all the drivers in phase at the listening position, you don't get this problem.
Last edited:
Yep, remember this - sum from 8 different mic locations up/down from midpoint of a line of 20 drivers midpoint 7.9cm, cone 5cm, flat panel, 3m distance to mic.
Combing is phase interference between soundwaves propagating from adjacent points in space.
Home of the Edge
Combing is phase interference between soundwaves propagating from adjacent points in space.
Home of the Edge
Why would the ends of the array "dominate" the combing? All drive units contribute equally to the summed response at the measuring point. If the interunit spacing causes a phase shift of 360 degrees, you get perfect summation, 180 degrees gives you perfect cancellation. The ends of the array (and all other drivers in the array) will have some phase shift between 0 and 360 degrees; it does not matter how tall the array is.
You are correct in that the summation is somewhat random along the front of the array, which gives rise to the +3db addition, unlike the +6db addition in lower frequencies. Now add one more thought to this thinking: phase shifts caused by interunit spacing are related to frequencies and interunit distances. Phase shift at 20 kHz is going to be twice the amount at 10 kHz. Similarly, phase shift between two 4" drivers is going to be twice as much as between two 2" drivers. What this does is it pushes the frequency at which comb filtering begins up or down. So, if you held everything constant, and doubled your interunit spacing, comb filtering will start one octave lower. If you doubled the listening distance, comb filtering will start one octave higher.
ra7: That's how I understand it. There is little (no?) relationship between the effects we are discussing and the height of the array - that high frequency combing effect is determined by the CTC spacing.
There are for sure measurable combing effects related to the height of the array which would occur in an anechoic environment even at lower frequencies - we just don't perceive them as such in a normal room. This would be where I agree with Murphy (or Toole) 100% that yes, there is combing but no, you can't hear it.
A lot of ideas about line arrays seem to relate to their far-field usage, thinking about off-axis lobes and narrowing at long distance and high frequency... in the near-field and in real (somewhat reverberent) rooms its a bit of a different beast. I do agree that the CBT elegantly solves a lot of these theoretical problems, and having not heard one I can't say whether the straight line vs curved line has anything to do with the effects I'm hearing... nor has distance been a real factor, nor has the length of the line.
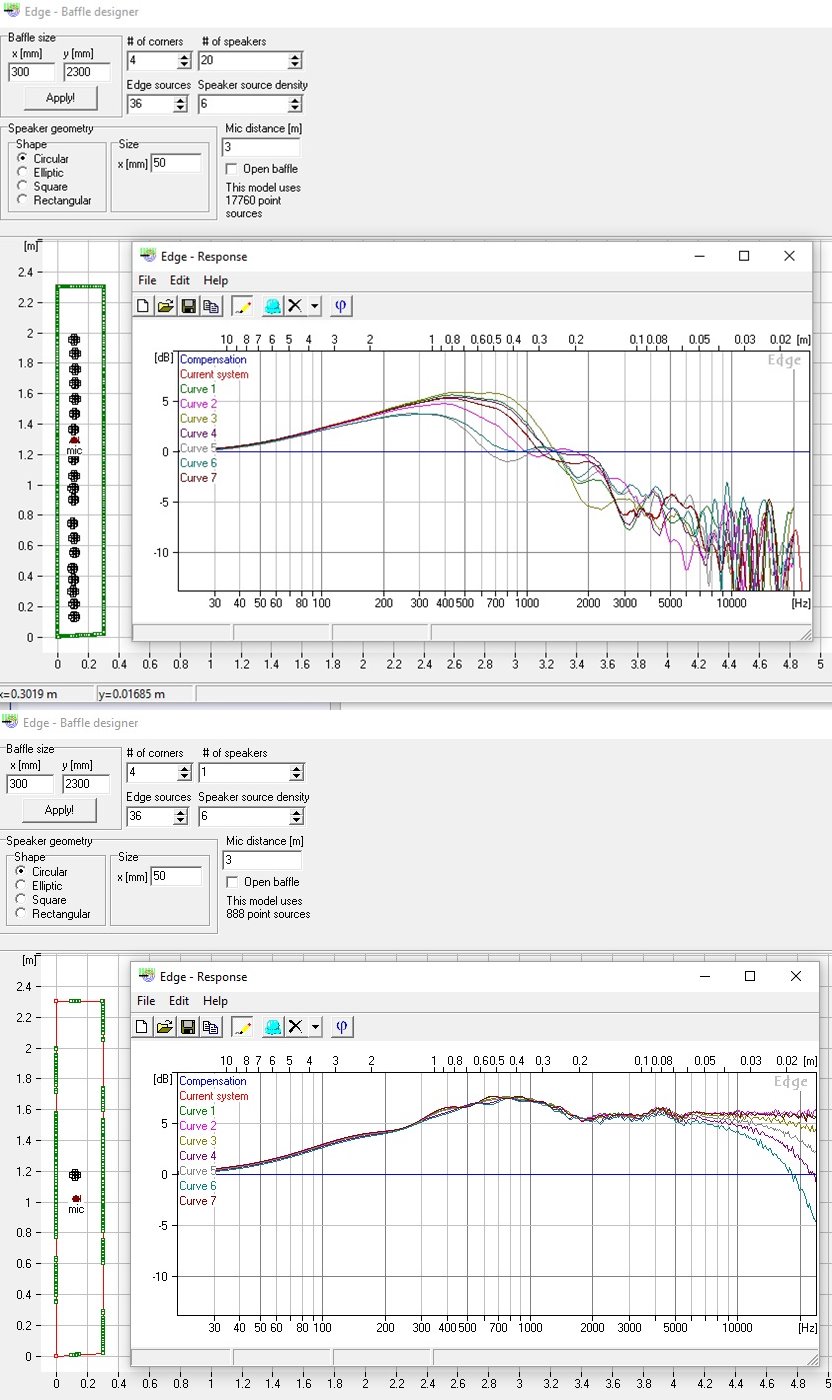
Aah you guys really should learn the Edge!
Here a collasche of four changing parameters
- numbers of drivers and spacing 1/2/6/12 drivers versus a single driver
- mic distance 1/2/3/4m (12 drivers)
- mic height center to top at 1m distance (12 drivers)
- mic height center to top at 4m distance (12 drivers)
Here a collasche of four changing parameters
- numbers of drivers and spacing 1/2/6/12 drivers versus a single driver
- mic distance 1/2/3/4m (12 drivers)
- mic height center to top at 1m distance (12 drivers)
- mic height center to top at 4m distance (12 drivers)
Attachments
Here is a short line with a tweeter that my friend has built, designed by Pekka Tuomela
A high-end story from Vantaa
A high-end story from Vantaa
- Status
- Not open for further replies.