Clarification of the final sentence:
Its area equals the little red area at bottom left, plus one of the large red areas (like the one on the bottom right), plus the area of a segment of the circle.
Its area equals the little red area at bottom left, plus one of the large red areas (like the one on the bottom right), plus the area of a segment of the circle.
Galu, I agree with your approach.
It should get to the left bottom red part area.
The trouble is, you need the area of a segment which is a messy calculation because of its ugly angle.
I did the same approach in the upper right to get the upper right red area. I fell on the very same segment calculation.
In post #1139 I show how I get at the upper right red part. There I comment about the ugliness of the segment area calculation.
In post #1140 I give a numerical answer.
It should get to the left bottom red part area.
The trouble is, you need the area of a segment which is a messy calculation because of its ugly angle.
I did the same approach in the upper right to get the upper right red area. I fell on the very same segment calculation.
In post #1139 I show how I get at the upper right red part. There I comment about the ugliness of the segment area calculation.
In post #1140 I give a numerical answer.
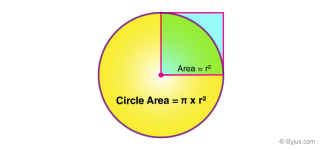
To get the red bottom right area, all you have to do is work out the area of a quarter of a circle then subtract it from the area of a square drawn on its radius as shown in the attached diagram.
Area of circle quadrant = (3.142 x r^2)/4 = (3.142 x 10^2)/4 = 78.55
Area of square = r^2 = 10^2 = 100
So the difference in area = (100 - 78.55) = 21.45
Area of circle quadrant = (3.142 x r^2)/4 = (3.142 x 10^2)/4 = 78.55
Area of square = r^2 = 10^2 = 100
So the difference in area = (100 - 78.55) = 21.45
Attachments
Last edited:
Yes, and I congratulated you on your answer! 😎
Your approach will agree with the contents of this link: Circle Sector and Segment
It shows how to get the area of the segment by subracting the triangular area enclosed by two radii separated by an angle θ.
Calculating θ is the problem!
Why would you need to calculate Theta?
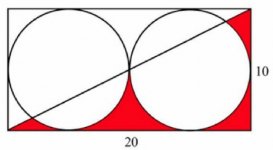
Calculate the area in Red:
Answer by symmetry: 100 - ( Pi X 5^2 ). Or 25 x ( 4 - Pi ).
Today's episode of Sesame Street was brought to you by the numbers 4 and 25, and the letter Pi! 🙂
Calculate the area in Red:
Answer by symmetry: 100 - ( Pi X 5^2 ). Or 25 x ( 4 - Pi ).
Today's episode of Sesame Street was brought to you by the numbers 4 and 25, and the letter Pi! 🙂
We're talking about calculating the little bottom left red area now (or little top right area!).
Last edited:
Yes, the small angle (x) in the isosceles triangle is given by tan x = 10/20 = 0.5
It's the same angle as the one at the left of the lower right angled triangle in the original diagram.
Attachments
I should perhaps stress that mchambin has already provided the answer in post #1140 - we are simply discussing the method of finding the answer.
Indeed, the fun is in the method of finding the answer.
Meanwhile, with Galu's methode, I calculated the area of the left bottom red area.
So I have the two hard to get areas of the small red parts.
I do not publish them to not spoil the fun.
A very accurate one for the lower left red area.
A crude value I gave in #1180 for the upper right red area.
I am pretty confident calculations are right because their sum is as expected.
Have fun and get them with many digits.
Meanwhile, with Galu's methode, I calculated the area of the left bottom red area.
So I have the two hard to get areas of the small red parts.
I do not publish them to not spoil the fun.
A very accurate one for the lower left red area.
A crude value I gave in #1180 for the upper right red area.
I am pretty confident calculations are right because their sum is as expected.
Have fun and get them with many digits.
TBH, mcchambin, I didn't really follow your method.
Cal's original problem was easy enough. Calculate the area in Red:
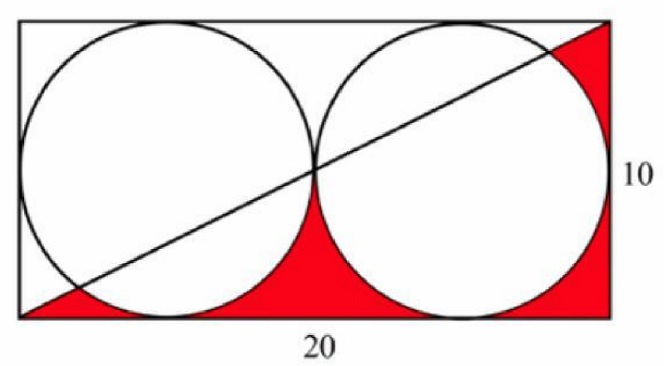
25 (4 - Pi) or 100 - 25Pi. 21.46018366...
Your segment problem was quite intractable to my most cunning methods. I suspect there is no algebraic solution. Only approximate numerical methods.
I found myself trying to solve 4 variables with 3 equations.
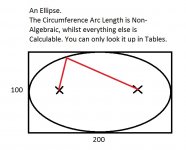
I think this has no exact answer algebraically. Just like the arc length or circumference of the Ellipse. You can only look it up in tables;
Elliptic integral - Wikipedia
Cal's original problem was easy enough. Calculate the area in Red:
25 (4 - Pi) or 100 - 25Pi. 21.46018366...
Your segment problem was quite intractable to my most cunning methods. I suspect there is no algebraic solution. Only approximate numerical methods.
I found myself trying to solve 4 variables with 3 equations.
I think this has no exact answer algebraically. Just like the arc length or circumference of the Ellipse. You can only look it up in tables;
Elliptic integral - Wikipedia
Attachments
Yeah, let's get out of here, before we get kicked out!
I suppose discussing the Covid is out of the question too. 😀
I suppose discussing the Covid is out of the question too. 😀
A chap walks into the optometrists carrying a suitcase.
He opens it to reveal the largest turd imaginable.
Shocked, the optometrist says, "Take that the heck out of here. It's a doctor you need, not an optometrist!"
The chap retorts, "I do need an optometrist. You see, every time I do one of these my eyes water."
He opens it to reveal the largest turd imaginable.
Shocked, the optometrist says, "Take that the heck out of here. It's a doctor you need, not an optometrist!"
The chap retorts, "I do need an optometrist. You see, every time I do one of these my eyes water."
This chap walked into Tesco tonight. Picked up a loaf of bread, 4 litres of milk and 4 tins of Beer. Customer Assistant Operative suggested a Plastic carrier bag...
The chap instantly declined, wishing to save the Turtles and keep in with GretaThunberg. Nothing he couldn't carry he thought. 🙂
How wrong he was. The ecologically friendly cardboard wrapper almost instantly collapsed, spewing beer tins onto the pavement (er, sidewalk for the cousins...). What was wrong with those plastic rings? Could it get worse? Yes, the ecologically economical flimsy thin tins immediately ruptured with a hissing noise,
Either it went to waste, or I had to drink it immediately. Well, it's an ill-wind that blows nobody any good. Hic. 😱
The chap instantly declined, wishing to save the Turtles and keep in with GretaThunberg. Nothing he couldn't carry he thought. 🙂
How wrong he was. The ecologically friendly cardboard wrapper almost instantly collapsed, spewing beer tins onto the pavement (er, sidewalk for the cousins...). What was wrong with those plastic rings? Could it get worse? Yes, the ecologically economical flimsy thin tins immediately ruptured with a hissing noise,
Either it went to waste, or I had to drink it immediately. Well, it's an ill-wind that blows nobody any good. Hic. 😱
Attachments
Just my 2 cents:
Subtract the area of one circle from the area of half-rectangle and you are done. Results in 21.46018366