#1120 puzzle:
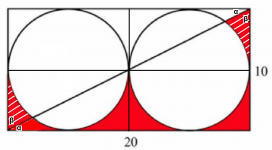
Total red area is half rectangular minus one circle.
For the individual red shapes, if we move the upper right on top of lower left, then the central part is half the total red area and the sides are quarters. Then the left can be split according to the diagonal angle.
Total red area is half rectangular minus one circle.
For the individual red shapes, if we move the upper right on top of lower left, then the central part is half the total red area and the sides are quarters. Then the left can be split according to the diagonal angle.
Alien implant for mind control.
Mine is much smaller and in my neck not my chest.
You'd better put it back or the aliens will come again to replace it.
Andy
Your warning came too late. They came back yesterday and put it back ... And aliens are SO FOND of the "back door". It hurts when I am sitting down ...
In case you have been living under a stone... 😀
Star Trek'''s William Shatner blasts into space on Blue Origin rocket - BBC News
Attachments
The shuttle is pretty boring compared to the exciting prospect of having your body disintegrated into its constituent subatomic particles then reconstituted elsewhere! 😱
The total red area is R²(4-Pi)
The right down red area is R²(1-Pi/4).
The middle down red area is R²(2-Pi/2).
I do not see how this gives you the upper right part area and the lower right part area.
The sum of these two areas is R²(1-Pi/4).
The lower left is smaller than the upper right.
The challenge is to find the individual areas.
I do not see an easy way to get this.
The same schematic with a few more lines drawn. The diagonal divides the circles so that the two parts of one equal the corresponded parts of the other. So the total red area is the lower part of the rectangular -one half- minus one circle i.e. 20*10/2-(5sq*π)=21,5.
The rectangular sides ratio 2:1 determines the α:β ratio so α=30 deg and β=60 deg. Moving the upper right red shape on top of the lower left fills a right angle. Then the red shape between the two circles is half the total red area =10,75 and each side is 1/4 =5,375. The lower original left is 1/3*5,375=1,79 and the upper right is 2/3*5,375=3,583
The rectangular sides ratio 2:1 determines the α:β ratio so α=30 deg and β=60 deg. Moving the upper right red shape on top of the lower left fills a right angle. Then the red shape between the two circles is half the total red area =10,75 and each side is 1/4 =5,375. The lower original left is 1/3*5,375=1,79 and the upper right is 2/3*5,375=3,583
Attachments
I am sure I can work out the area in red, but the page may be too small to show the exact answer. 😀
Star Trek'''s William Shatner blasts into space on Blue Origin rocket - BBC News
Captain Kirk was wondering if his trip into Space could be recreated in 3D media or something so everyone can go there, without wasting money on Rockets. I have already done it!
Enjoy. We are all Astronauts now! 😎
I've not solved this yet but it looks within my means.
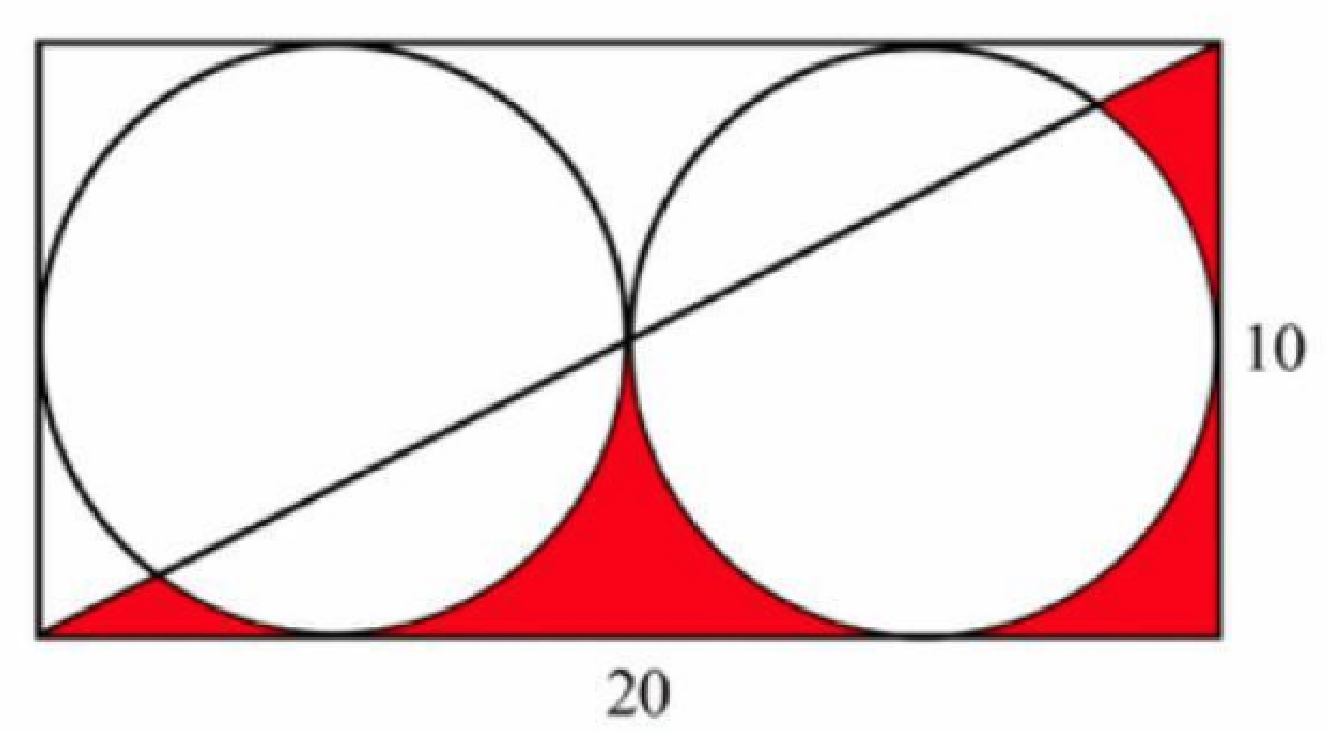
Find the area in red. Let's assume the circles have a diameter of 10 although it looks slightly off in the pic.
Star Trek'''s William Shatner blasts into space on Blue Origin rocket - BBC News
Captain Kirk was wondering if his trip into Space could be recreated in 3D media or something so everyone can go there, without wasting money on Rockets. I have already done it!
Enjoy. We are all Astronauts now! 😎
Attachments
this is not entirely correct, actually.
if the smaller side of the right triangle is half the hypotenuse, then your angles would be correct...
I admit I'm using rusty school geometry. Could you elaborate if it doesn't take too long, please?
Simply further divide the figure into eight squares.
The area of a quadrant of one of those squares is (10x10)/4 = 25
The area of a quadrant of one of the circles is (3.142 x 5^2)/4 = 19.635
So the area of the bottom right red area = (25 - 19.635) = 5.365
So the total red area is (4 x 5.365) = 21.46
It's easier if we divide up the big rectangle into 4 rectangles, each 20 long by 10 high.
Then add the bottom left to top right diagonal of the rectangle.
Now focus on the little bottom left triangle.
Its area equals the little red area at bottom left, plus one of the large red areas, plus the area of a segment of the circle.