Removing Loudspeaker Group Delay using reverse-IIR filtering

Jump to Latest
#82
Hi, yeah, I have no idea what it takes from the algorithm perspective.

Rudimentary search finds github libraries for non-linear curve fitting, also here is something https://observablehq.com/@christophe-yamahata/nonlinear-regression-in-javascript but I have no idea whether these are what you need. There is libraries to read data and so on, so I'm very optimistic it could be made relatively easily, although devil is always in the details.

Thought to post just in case you continue excersize with web stuff 🙂 Web is kind of universal, you can do pretty much anything there, and it's almost platform and device independent, easily accessible and monetizable, and infinitely more flexible and usable than excel 🙂 assuming there is some internet connection.

edit. well, perhaps the excel spreadsheet is just fine compared to amount of work it needs to put on the web. Kimmosto might add this to VituixCAD as well if you hint about it to him.
 
Last edited:
#83
I once made a spreadsheet for designing analog group-delay equalisers using allpass filters. I did the approximation of the pole frequencies and Q values manually by trial and error. With a little practice it works quite well. An automatic approximation algorithm is of course sexier than that ......

Regards

Charles
 
#84
For a web app you need to have a bunch of stuff running on a web server as a sort of "back end" - the code that does the fitting, etc. That's really not something that I could set up.

The Excel based alternative I had in mind is an adaptation of one of my ACD Tools spreadsheets. I have lots of experience with the Excel Solver and I am relatively confident that it would work well. I will play around with it in the next couple days when I have time and see what I can come up with.
 
  • Like
Reactions: tmuikku and wchang
#86
OK, this is a more complicated fitting problem that I first imagined. Once you create a group delay curve that is like a multiway loudspeaker and that would require three or four different allpass stages it does arrive at a relatively decent fit but I cannot recover the exact parameters of the allpass filters I used to generate the GD curve.

If one just does it "by eye" it seems there are many similar close approximations to the group delay curve, especially if one is OK with just capturing the general trend and not matching it exactly. So the problem may be is a bit ill-defined in general.

I might play around with normalizing the group delay curve by an audibility threshold that is a constant 1 msec from 1kHz and up, and increasing with 1/f below. This will help even out the goodness of fit metric as a function of frequency.
 
#90
Each second order allpass has two parameters: F and Q. The first order allpass has only the F. So I tried a step-wise fitting approach:

1. enter some sane but not necessarily correct values for all Q and F values
2. Step 1 is to fit only the F values while keeping the Q values fixed
3. Step 2 is to continue the fitting, but now include the Q values.

This 2-step approach seems to be more reliable. Because the Q values are omitted, there are half the number of fitting parameters in step 1 and this makes the process easier for the GRG algorithm. Once the F values are close, you can do the full monty.

I will do some more experimenting with this same approach to see what happens.

@uriy-ch : yes, sometimes the group delay at low frequencies is very noisy or you cannot get it from the measurement. It can can be estimated using a Thiele-Small box model, etc. It's not necessary to correct 100% of the group delay of the system.
 
  • Like
Reactions: wchang
#91
1. enter some sane but not necessarily correct values for all Q and F values
Click to expand...
As a general rule I found that it is convenient to start with equidistant (on a linear scale !) pole frequencies and Q values rising with frequency.

The cyan trace is the GD of the crossover itself. The blue one is the sum of the crossover and the EQ, and yes the 5th allpass' own trace went missing somehow on the diagram.

And I also once found a formula in a book on filter theory giving a coarse estimation of the total order of allpass that is needed for the EQ. If you want to have a very exact end result you need a higher order if it doesn't have to be as accurate you can go for a lower total order.

Minorder=1 + 2 * GDmax * BW

With GDmax equal the maximum amount of group delay that has to be equalised and BW the bandwidth over which the GD linearisation has to be achieved.

For a LR2 @ 2 kHz for example EQed up to 20 kHz you need 1 + 2 * 106 us * 20 kHz = 4.24 i.e. 4th order for a less accurate result and 6th order if the curve fitting has to be more accurate.

Regards

Charles
 

Attachments

  • Allpass-EQ.gif
    Allpass-EQ.gif
    150.6 KB · Views: 54
Last edited:
#92
@phase_accurate Can you send me the data for "GD of the crossover" shown in the plot, above. I would like to try and fit it.
EDIT: actually, nevermind. No need to send it.

So far I have been working with a GD curve that is generated by the following:
AP2​
AP2​
AP2​
AP1​
F​
​
100​
​
500​
​
2000​
​
30​
Q​
​
0.707​
​
0.707​
​
1​
​

I guesstimate you would get this from the following:
The AP1 is like the group delay of the woofer itself
The AP2@100 mimics the GD from an LR4 crossover at 100Hz
The AP2@500 mimics the GD from an LR4 crossover at 500Hz
The AP2@200 mimics the GD from a steep crossover at 2k Hz

Looks like the following. I can get a good fit when I use the 2-step method.

crude system GD plot and fit.png
 
Last edited:
#94
@gberchin I did something similar... a bit more, ahem, recently (!) using Thiran All-Pass filters. Usually around 10th order. The nice thing about them is that there is a closed form equation for designing the filter! From the looks of your plot, the group delay is about the same result - very flat (maximially so for Thiran AP) and then a peak or dip just below Nyquist.

Info:
https://ccrma.stanford.edu/~jos/pasp/Thiran_Allpass_Interpolators.html
 
Last edited:
#95
@phase_accurate Can you send me the data for "GD of the crossover" shown in the plot, above. I would like to try and fit it.
Click to expand...
The sheet spits out the frequencies in relative values. The assumed LR2 crossover behaves as a first order oder allpass with a pole frequency of 2 kHz. The provisional 2nd order EQ poles and frequencies are:

1st fpole=3.6 kHz, Q=0.9
2nd fpole=6.4 kHz, Q=1.5
3rd fpole=9.2 kHz, Q=2.1
4th fpole=12 kHz, Q=2.9
5th fpole=14.5 kHz, Q=4.0

Keep in mind that these are just quick and dirty values from an example. A little further trial and error would be necessary to get more accurate.

Regards

Charles
 
#97
It looks like you are fitting N second order allpass filters to the GD curve. Why would you not fit just a first order allpass with Fp=2k Hz?

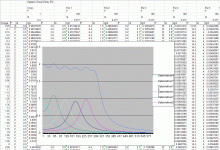
Below is a pic of the interface for my Excel fitting workbook. This is an adaptation of a general filter tool. Each column is a different filter. There is a "type" field for which first order allpass is type 3 and second order allpass is type 23. Then you just fill in the Fp and Qp values below. You can add as few or as many filters as you wish (up to I think 20). Then you point Excel's GRG solver to optimize the Fp and Q values, and to use a cell on the sheet that holds the fitting error.

Filter descriptions.png


You can see that the values I get by fitting the GD curve with the 2 step method are very close to the exact values I listed earlier. This seems to be repeatable using some relatively random but sane starting values for the frequencies and initially setting all the Q values to 0.6, which is close to maximally flat for each AP2 section.
 
Last edited:
#98
CharlieLaub said:
EQing drivers flat, at least a couple of octaves beyond the desired passband edge frequencies, tends to make the phase response within the desired passband region flat with a phase angle near zero (assuming they are time aligned). This sort of takes their phase contribution out of the design process, and all you have to worry about is the phase response of the crossover filters. It's a worthy approach. But it is also possible to make adjustments to driver phase using allpass and digital delay without having to apply lots of gain where the driver's response is rolling off just to flatten the phase...

in the end, as long as the drivers are in relative phase alignment in the crossover region all is well. The phase response outside of their respective passband is not important.
Click to expand...
(Hi, bold emphasis mine)
I haven't had best luck trying to independently linearize a driver's phase. It never comes out as well as using out-of-band minimum phase flattening. Phase-only corrections have made more mag ripple, and given less ability to change crossover orders and frequency.
I think phase-only corrections of drivers is suboptimal, and is one of the misuses of FIR (or of an equivalent all-pass strategy.)

I've also found that an apparently large gain applied to out-of-band flattening is mainly illusionary. Because it gets negated when applying the crossover, as long as final acoustic crossover order is wisely chosen.
By wisely chose, I mean what would be the desired acoustic xover order irrespective of the implementation method.

Both the flatten-first out-of- band first and then apply the xover method; or the common method of choosing an electrical crossover and then nudging it with PEQs, shelves, all-pass, etc, towards the desired acoustic xover ...... both techniques if properly implemented ....... end up being the exact same net filter.

For me, it's a matter of which one is easiest to implement initially, and then more importantly, which one allows alterations of xover frequencies, types, and orders without a complete EQ redo. Go flat first, wins hands down ime.
 
#99
Ah I forgot to mention how to get data into the fitting workbook...

There is a worksheet that is completely blank. The use pastes into columns A and B the group delay (col B) versus frequency (col A) data. The data can consist of any frequency range and any number of points up to the spreadsheet maximum rows. This data is interpolated onto the frequency grid used in the rest of the workbook. This makes it very versatile in terms of what sort of data can be worked on and this should makes it simple for a user to fit e.g. measured data. The group delay must have the units of milliseconds.
 
You must log in or register to reply here.
Top Bottom