First, when I run my code with nonlinear air compliance for SL's cases I see about the same magnitude of air spring distortion as he gets from his simple analysis.
Second, there is a real possibility that the higher distortion seen in SL's measurement could be the results of the woofer box walls flexing. If you look at SL's Thor design;
you can see that he is not real big on building cabinets with stiff walls.
I already did, power. Almost no current through the bare driver at Fs and lots of current through the driver in the box an octave below Fb. 4x the voltage for equal excursion and lower impedance below Fb equals way more current (VC heating).
Last edited:
Nah, the resonance frequency of Balic Birch panels that size would be WAY above 20 Hz.
Wall flexing at those frequencies doesn't necessarily mean that they are resonating at those frequencies.
Dave
Depending on which frequency the distortion in question, the surround effects is often forgotton.First, when I run my code with nonlinear air compliance for SL's cases I see about the same magnitude of air spring distortion as he gets from his simple analysis.
Second, there is a real possibility that the higher distortion seen in SL's measurement could be the results of the woofer box walls flexing. If you look at SL's Thor design;
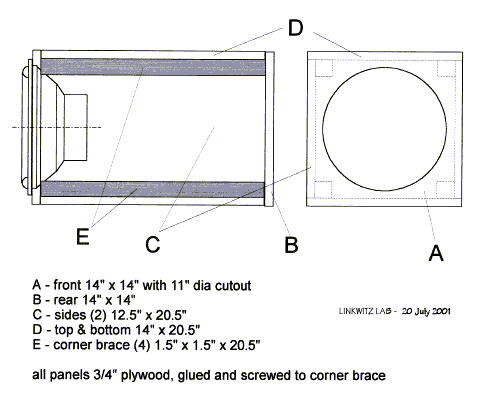
you can see that he is not real big on building cabinets with stiff walls.
Furthermore. BL and Kms related distortion should not be a factor forgotton.
Yes, the air is asymmetrically nonlinear but that does not mean that there are only even order harmonic distortion.
Obviously there are compressive effects (on the drivers motion) in both directions as the nonlinear air spring is exercised hence also symmetrical and odd order harmonic distortion.
These numbers are simulated by Svante:
The mentioned SPL are inside the box and does not represent very high levels outside the box.
I don't see why measurements gear wouldn't detect these levels.
/Peter
Yes.
What about at or around resonance?
The whole range of a transducer effects the transient response. A transient response (of the right type at least) give you all information about phase and frequency response, allthru the passband.
I don't see how the compliance and fundamental resonance could be taken out of the equation. Change the compliance and the behaviour in time and frequency domain is altered = the transient response is changed.
/Peter
According to the numbers simulated by Svante:
..and some calculation for one example from another guy the SPL at 3 meters which correspond to the internal box pressure of 160dB is aprox. 75dB SPL @20Hz.
/Peter
..and some calculation for one example from another guy the SPL at 3 meters which correspond to the internal box pressure of 160dB is aprox. 75dB SPL @20Hz.
/Peter
Here is a figure showing some additional simulations.
In all cases the excursion is the same. Air compliance is correctly modeled. Suspension compliance is a model with function that is symmetric and nominally constant for smaller excursions but then decreases at the specified Xmax is approached or exceeded. For the parameters used we see that air introduced both odd and even order distortion. The suspension can only introduce odd order distortion since it is symmetric. Note the interesting effect that when both the air spring and the suspension compliance are included 2nd order distortion is reduced compare to air spring alone, but all other distortion components increase. BL nonlinearity in not include.
The box size and excursion were intentionally chosen so that the air spring would exhibit significant distortion. Other parameter choices can yield very different results. I don't think it is possible to make a general statement when dealing with small boxes and high excursion woofer.
Aside from the additional effect of BL nonlinearity, dlr indicated what I meant by wall flexing. The walls need no be resonating but simply flexing under the pressure forces. Under static conditions the flexing may result in a linear stress/strain relationship, but under dynamic and/or oscillatory conditions the relationship could well be nonlinear.
So its NOT air spring distortion at all and the example is meaningless as regards support for air being "highly nonlinear".
I just modeled the Peerless XLS 12 in WinISD. At 20 Hz, to get 1" p-p excursion, it takes about 8 VA in an infinitely large box and 76 VA in a 50 liter box.
I did this stuff years ago. My spread sheet is dated 2005. 🙂
Earl,
Air spring nonlinearity is not dominated by a squared term. The nonlinear compliance goes like Cba = (1 + Sd x/ Vb)^(k+1)
the spring term in the governing eq goes like
x/Cab = x / (1 + Sd x/ Vb)^(k+1)
Even in the isothermal case,
X/Cab = x / (1 + 2 Sd x/ Vb + (Sd x /Vb)^2)
That contradicts post 366 by Drew, the bottom of which I agree with and it states "Primarily 2nd order".
There will be higher orders because of the expansion of the nonlinearity in the denominator, but the higher order terms will not be very significant and there will still only be even orders.
At any rate, I don't understand your terms so I cannot comment further.
No offence to Drew, but my result is what theromdynamics says. I tend to believe thermo.
[edit] I checked Drew's post. It is just the engineering approximation that Linkwitz derived under the assumptions that 1) the change in volume is small compared to Vbox and 2) that distortion is 2nd order. Large woofers in small boxes undergoing high excursion violates those assumptions. He is assuming what the answer is before hand. "If the distortion is 2nd order, and If the change in V is small compared to Vbox, then." It is not "physics".
As far as understanding my result, it follows directly form PV^k = const.
Last edited:
I don't agree that the assumptions are violated, the change in V is always small compared to V unless you are talking about an extreme example in which case I'd say that it doesn't apply.
What is X/Cab ?
The point is in a Taylor expansion of PV^k about P0 what is the lead term, and how small are the others. I agree with Drews post that the lead term is quadratic and all the others are small given the reasonable assumptions being made.
I took Nonlinear Acoustics at Penn Sate and there we always viewed air as pretty much quadratic. Even water does not have significant terms above the second. Compared to water, air is extremely linear.
Last edited:
First of all, we agreed a while back that for small excursions the air spring is basically linear and that we could ignore nonlinear effects altogether. The question then becomes, when is the nonlinearity significant, and, if you like, to what order? I don't think that assuming dV is small compared to V is satisfactory when looking at today's small box, high excursion subwoofers. There are 12" subs in 1 ft^3 boxes with excursion exceeding 2" PP. That's approaching dV = 10%.
In my equation X is excursion from the rest position. Cab is the compliance of the box. In the linear case, Cab = Vbox /(k Po Sd^2). This is the reciprocal of lead term in the Taylor expansion of P for PV^k = const. The exact expression for the nonlinear box compliance term in the PDE governing the drive motion is
X/ [Cab * (1 + Sd X/Vo)^k+1]
as compared to
X /Cab in the linear case. I wrote this several posts ago. All my simulations include the full nonlinear term.
The exact expression can be expanded in a power series if you like and you can include as many terms as you like. Obviously the usual approximation for box simulation is keeping only the 1st order (linear) term. If you take the approximate route then it is impossible to tell what effect, if any, the higher order terms which have been omitted might have as excursion increases. As we previously agreeded, except for large excursion woofer in small boxes, the linear approximation is sufficient. But that leaves in question when are the nonlinear terms important, and which order terms? If you solve the exact problem numerically (which takes no more effort) then there is noting to worry about. If the distortion is primarily 2nd order that will come out. If higher order HD components become important then they will reveal themselves.
Look at my post 409. The figure on the lower left shows what happens when excursion gets large in a small box subwoofer. Certainly at low excursion all distortion becomes negligible. As excursion increases the 2nd order term shows it's effect first, but as excursion increases further the higher order terms come into play, and, as I am sure you realize, the higher order terms will increase at a faster rate than the lower order terms. Interestingly, if I expand P in a Taylor series and keep only the 1st and 2nd order terms it turns out to be a more complex problem (numerically) to solve that just keeping the full nonlinear expression for air compliance.
Also examine the figure in the lower right where both suspension and air nonlinearity come into play. Here the 2nd order HD previously associated with the air actually decreases but the 3d order HD, previously associated only with the suspension (figure directly above) increases, as do all the higher order terms. I don't believe that behavior is revealed if the full nature of the air nonlinearity is not included. Note that in all these cases the excursion is identical.
John
None of what you say has anything to do with the discussion as I see it. I said that the box compliance linearizes the driver. You commented that this wasn't true because the air compliance is more nonlinear than the driver compliance. (You seem to have backed off from this position now.) You are now backing into simply saying that in extreme cases the air can be "significantly" nonlinear.
My original statement stands and you have done nothing to refute it except to go to extremes where you statement is maginally true.
None of what you say has anything to do with the discussion as I see it. I said that the box compliance linearizes the driver. You commented that this wasn't true because the air compliance is more nonlinear than the driver compliance. (You seem to have backed off from this position now.) You are now backing into simply saying that in extreme cases the air can be "significantly" nonlinear.
My original statement stands and you have done nothing to refute it except to go to extremes where you statement is maginally true.
- Status
- Not open for further replies.