What if it's a damped ported enclosure? Like an Aperiodic Bass Reflex. I guess it all depends but it would seem that in that situation for transients the air would stay linear momentarily er I think.
For all practical purposes in audio air is always linear.
As to the air pressure on the cone, the wavelengths of sound in air are much bigger than those in the cone, so there is little effect. The only effect that I know of that is significant is the fact that the surround tends to be softer than the cone, so the same pressure will cause a greater effect on the surround than the cone. This is the forcing function that tends to driver the edge resonance.
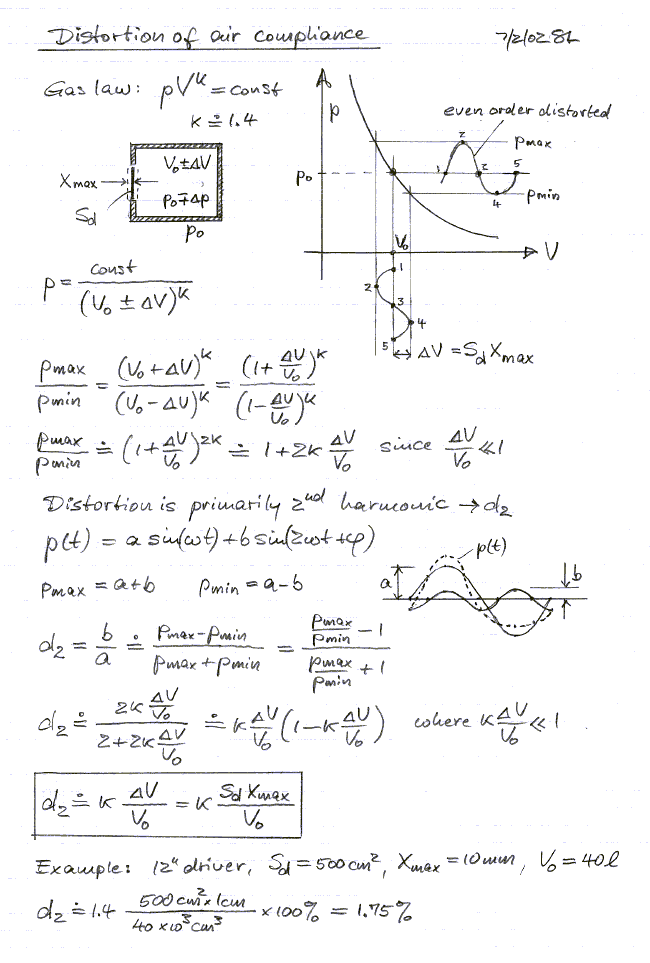
I have to disagree with the air spring in a box being linear. I worked on this several years ago. I agree that if the air spring is linear then a driver in a box can have lower distortion than a driver in free air. However, the difference is negligible. But the air spring is not linear. The nonlinear compliance of the air spring can be shown to be
Cabnl = Cab(1 + Sd xr /Vo) ^(k+1)
where Sd is the cone area, xr the excursion and Vo the box volume. K is the polytropic exponent (between 1 and 1.4 for air depending on whether the compression/expansion process is isothermal or isentropic). Note that the nonlinearity is a function of Sd times xr or the swept volume. Since for at a given frequency the SPL level is directly proportional to the swept volume, distortion due to the air spring is also proportional to SPL. Additionally, since for a given SPL swept volume increases at 1/f^2, air spring nonlinearity increases quadratically as frequency decreases. And since the air spring nonlinearity is a function of 1/Vo, smaller boxes lead to higher distortion.
Another issue is that suspension compliance tends to be symmetric about the driver rest position. The result is that suspension compliance generated distortion tends to be odd order. The air spring exhibits asymmetric nonlinearity with the result that associated distortion is even order.
In the end, when all these affects are summed up the effect of the air spring on reducing inherent driver distortion negligible, even if the air spring is considered linear. The distortion generated by the nonlinearity of the air spring tends to only be significant in subwoofers placed in small enclosures.
Here is an example of a driver in free air compared to the same driver in a 58 L box at the same frequency and excursion. The figure on the left is free air. The figure on the right is an over lay of the in box result considering the air spring as linear or nonlinear. Tho open symbol showing 2nd order distortion is the result of the nonlinear air spring. Odd oder distortion is effectively the same in all cases. Even order distortion arises only form the air spring in this example. Suspension compliance is real drivers can, of course be asymmetric and BL nonlinearity is generally also asymmetric. Thus even in free air a real driver will exhibit both odd and even order distortion.
An externally hosted image should be here but it was not working when we last tested it.
Just one more reason to use big boxes
Just one more reason that big, high efficiency speakers sound better than little tiny ones
Just one more reason that big, high efficiency speakers sound better than little tiny ones
I agree with this, not much of the rest. And if this is true, then its ability to make a difference depends on the relative values of the driver and air springs, which I also said.
To use two of Sigfreid Linkwitz's measured examples, we have dipole which is close to free-air
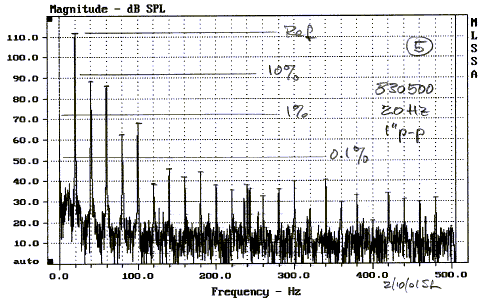
context Alternate drivers 3
and in a small (50L) box for Thor
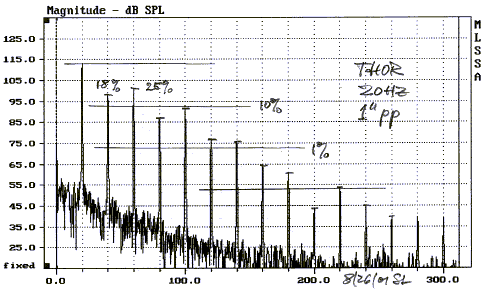
context Woofer measurements
with distortion much worse than SL would estimate
Last edited:
The question is: Is the 1.75% 2nd order distortion (MAX under full possible excursion) less than or greater than that caused by the suspension at the same frequency under the same excursion. I think less than. In which case the air is the more linear and it will tend to linearize the mechanical compliance. Now it is POSSIBLE that the compliance of the driver is incredibly linear, but that's the exception NOT the norm. I'll stand by my original claims.
Aperiodic type designs can be made to lower the system resonant point. Like a non-ideal spring model with damping. With this kind of design, there is a open port, but I would hardly call it bass reflex. Due to higher compliance of this kind of design, the transients should be nice. However, the tradeoff seems to be that there will be a phase difference between the port and the radiator over a certain bandwidth which can introduce distortion.
Well I guess I was talking about a specific hybrid design. Pretty sure that would be a more accurate title for the type of speaker I use. It has a tube but at the throat it has a net which breaks up the air going into the tuned port. But I suppose that is more on the Bass Reflex side than aperiodic. Still I guess I was wondering how you would model something like that.
OK Soongsc - you say that you want to learn. Compliance can't have anything to do with "transient response". Any speaker has three frequency regions - compliance controlled, resistance controlled and mass controlled. Compliance below resonance, resistance at resonance and mass above resonance. Transients are high frequency aspects of a signal, hence they act only in the mass controlled region. Compliance has nothing to do with transients, only mass counts.
Okay, so if you can answer my questions in a direct manner one by one, it out be much appreciated.
Going back to basic physics. If we use the same force to push against a spring of K vs 2K spring constant. What is the difference in displacement? Now don't jump ahead please.🙂
Last edited:
Earl is correct George. If you look at the mass, spring damping system you will find that the mass term goes like (w/wo)^2, the damping like w/wo and the spring is order (1). So the spring term is significant only when w is small. When w is around wo (resonance) all three terms contribute equally. When w gets large, only the mass term is significant.
To answer your question to Earl, obviously if the spring is twice as strong the displacement will be 1/2 has great for the same force. But if it is a spring mass system and the frequency is very high, the force required to accelerate and decelerate the mass is much, much greater than the force required to compress the spring.
Last edited:
John, I think it takes a few questions to understand the exact model our thoughts differ on. This is why I'm asking questions in a series. Most models considered in speaker design are lump parameters.
For the next question. Regarding the remarks qouted, when we talk about transients, what are we talking about? The onset of response to an input? Or the response from onset to settling? What frequency range?
Let's not get into the "who's right or wrong" issue, but really understand whether we are talking about the same thing first.
Last edited:
Except that near resonance, the mass and compliance impedances are equal and opposite and therefor cancel leaving the response dominated by the resistance term alone.
The "transient response", in a strict physics sense, is that part of the response that dies out after a time leaving only the "steady state" response. In math parlance it is the specfic solution to the inhomogeneous Diff EQ. Now, if you are talking about the impulse response, the steady state is zero, so the entire waveform is the transient response.
The frequency range for a loudspeaker would therefor be the range above resonance because below resonance there is very little contribution to the sound radiation response. This would make the transient response mainly mass controlled, but since points near resonance contribute, the resistance would contribute as well. The compliance enters in only to set the lower limit of the response, but does not ever contribute where the response is significant.
While your interpretation is true, this does not seem to be what the original referenced remark was trying to express. Don't you think so?
I think Key was trying to express the onset part of the response.
Although this seems to be getting a bit ahead of me, it seems appropriate to ask another question:
Are you saying, that even for the same driver, if only the spider stiffness were changed such that the resonance were increased to twice the frequency, does this mean the frequency response will not go as low as the original driver in actual application?
Not at all Earl. If that were the case there would be no resonance. At resonance energy input to the system is conserved and exchanged between the mass element (capacitance) and the compliance element (inductance). In the absence of any resistive element no energy would be lost and the resonance would build to infinity (or self destruction). The resistive element limits the growth of the resonance. All three components are of equal magnitude. None dominates. The impedance at resonance is purely resistive because, but the restive element is not dominate.
The covering PDE in dimensionless form for a sealed box system is
F(t) = x” + Ω (1/Qms + 1/Qes) x’ + Ω^2 (1 + α) x
where Ω = ωn / ω , and α is the compliance ratio, Vas/Vb.
Ω = 1, at resonance.
Thats just symantics John. What I said was correct and consistant with the literature. The region arround resonance IS called "resistance controlled" because the level of the response in that frequency range is principly a function of the resistance.
George - you have to know that this is true - its fundamental. To double the resonance the stiffness would have to go up by four times. The passband response would be unchanged, the resonance peak would rise and below resonance would fall. Since resonance is higher, of course "the frequency response will not go as low as the original driver"
It seems to me that the operative part in your statement is "resistance controlled". It's not semantics, the magnitude of the resonance is limited (controlled) by the resistance with the peak being the point at which both inductive elements are equal. I don't see why you're minimizing this by calling it semantics.
Dave
- Status
- Not open for further replies.