To mitigate its effect, it has to be present.To mitigate
Unless you have yourself an infinite baffle, diffraction is necessary.Diffraction is evil.
TNT - If you run a VituixCad baffle diffraction simulation of a spherical baffle and a square sharp-edged baffle of the same area, you will see that the square baffle has much more high frequency diffraction ripple. The spherical baffle has almost none.
But both will have the same level of low frequency diffraction, the transition from 4-pi to 2-pi radiation. This effect is usually called baffle step, and it is caused by diffraction.
Low frequency diffraction (baffle step) = good diffraction, or at least, unavoidable diffraction
High frequency diffraction (ripple) = evil diffraction
But both will have the same level of low frequency diffraction, the transition from 4-pi to 2-pi radiation. This effect is usually called baffle step, and it is caused by diffraction.
Low frequency diffraction (baffle step) = good diffraction, or at least, unavoidable diffraction
High frequency diffraction (ripple) = evil diffraction
https://www.diyaudio.com/community/...-spherical-speaker.374278/page-8#post-7065195
This post might clarify things...
This post might clarify things...
Isn't the "baffel-step" rather the loss of acoustical impedance due to the size of the baffle and the involved wavelength rather than a reflection/bounce problem? And this is why an infinite baffle (don't mean closed box NB!!!!) don't have a baffle-step problem.
//
//
The purpose of a sphere is to create diffraction.
The purpose of the sphere is to negate diffraction.
Both happen, depends what frequency you are talking about.
A well done sphere will reduce diffraction at higher frequencies but as they approach the size of the ball you get baffle diffraction loss (baffle step).
dave
Isn't the "baffel-step" rather the loss of acoustical impedance due to the size of the baffle and the involved wavelength rather than a reflection/bounce problem?
Diffraction is different from reflection. Imagine a spherical baffle with a small full range speaker mounted in it, suspended in free space. At low frequencies, the system will behave almost omnidirectionally. The process where low frequency waves bend around the sphere to radiate in all directions is diffraction. At higher frequencies, where the wavelength is smaller than the baffle, the diffraction occurs smoothly across the whole radius, rather than at a single sharp edge. Just because it happens smoothly does not mean that diffraction is not present.
If we want to be precise in our language, we would say that a spherical baffle has a very smooth diffraction response. But it is not really correct to say that it has no diffraction.
One way of mitigating diffraction is by rounding sharp corner on a box where a transducer is emitting sound waves. A wave is excited, now it is approaching an edge... what will happen - will something mitigate it from diffracting or will diffraction happen? Yes - someone just filed off the corner before the wave hit it and the upcoming, potential effect was mitigated - and hence, it is not present. :-DTo mitigate its effect, it has to be present.
Unless you have yourself an infinite baffle, diffraction is necessary.
//
Imagine? You mean like the two I'm steering at right now of which one is depicted in #237 🙃
So you mean that why deep bass isnt directive is due to diffraction?
//
//
So you mean that why deep bass isnt directive is due to diffraction?
//
A round baffle cant be compared to a sphere - if if the sphere is "round". I don't think VituixCad does sphere... or?TNT - If you run a VituixCad baffle diffraction simulation of a spherical baffle and a square sharp-edged baffle of the same area, you will see that the square baffle has much more high frequency diffraction ripple. The spherical baffle has almost none.
But both will have the same level of low frequency diffraction, the transition from 4-pi to 2-pi radiation. This effect is usually called baffle step, and it is caused by diffraction.
Low frequency diffraction (baffle step) = good diffraction, or at least, unavoidable diffraction
High frequency diffraction (ripple) = evil diffraction
//
Agree!If we want to be precise in our language, we would say that a spherical baffle has a very smooth diffraction response. But it is not really correct to say that it has no diffraction.
//
ie making the front of the box look more like a hemisphere.One way of mitigating diffraction is by rounding sharp corner on a box...
dave
I'd seen an AES paper describing 3 undesirable reflection type components created by a horn baffle.. I meant to save it and have been looking for it for a long time.. High order modes, diffraction and something else.. Does anyone have the paper that could share it or provide a link? not spherical but thought i would ask here.
VituixCad will not perfectly model a sphere, but it can get a close approximation.A round baffle cant be compared to a sphere - if if the sphere is "round". I don't think VituixCad does sphere... or?
In Vcad, we can model a 200 mm diameter circular baffle, then give it an edge radius of 100 mm. This effectively makes it a hemispherical shape.
It seems to, yes.This will give the Olson results?
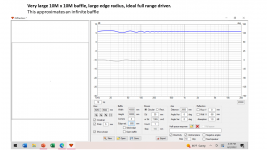
The first graphic shows the VituixCad approximation of an ideal full range driver in a 10 m x 10 m baffle with a very gentle 200 mm edge radius. This approximates an infinite baffle, but even here the simulation predicts some low level diffraction ripple.
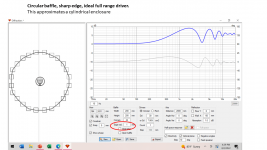
The second graphic shows an approximation of a circular baffle with a sharp edge. This approximates a cylinder of diameter 200 mm, with the driver mounted on the circular face.
The third graphic shows an approximation of a circular baffle with an edge radius equal to the circle radius. This is the Vcad approximation of a sphere.
In the second and third graphic, we clearly see that diffraction is causing a 6 dB loss as the frequency falls from 1000 to 100 Hz. However, in the sharp edge circle, there are other diffraction effects which are disruptive.
Attachments
Last edited by a moderator:
But it hasn't gone away, It's just spread out.you will see that the square baffle has much more high frequency diffraction ripple. The spherical baffle has almost none.
(BTW, you shouldn't necessarily judge diffraction based on response ripple which you might see on a simulation like this. Diffraction can be an audible problem and also be difficult to identify by looking at response.)
Also of interest is the differences it can cause in the off axis response. That difference can be audible too.
To me the second and third graphs show baffle step with and without diffraction. Baffle step is a 2pi - 4pi transition and involves the entire baffle. Diffraction is edge scattering when the baffle is significantly larger than the wavelength and only occurs at the baffle boundaries. I don't the benefit of conflating the two.In the second and third graphic, we clearly see that diffraction is causing a 6 dB loss as the frequency falls from 1000 to 100 Hz.
- Home
- Loudspeakers
- Multi-Way
- How to build a spherical speaker?