Member
Joined 2019
Audiophiles have a notion of how much force a 'gram (-force)' is from adjusting and using their tonearms -- they can more readily have an intuitive feel for the magnitude of forces you're discussing.
OK, I will try to use gram-force where proper (I can never use "gram" for a force, this will make me feel really bad.. ). But for the mg-force region I could use dyne. As long as the audiophiles have not a feel for this force magnitude. 🙂
Member
Joined 2019
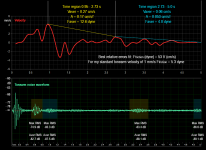
The Eora 3 measuring installation
The new swing has the same length of 33 cm, but 43 g are added to the swing base, so that the total moving mass rises to 75 g. This results in longer durations of the visible decaying oscillations. The friction force is not affected by the rise of the mass. The video is now taken with my digital microscope camera and allows higher measuring precision, of the order of 0.03 mm. I include a link to the microscope video. Another new feature is the parallel video and audio recording, so that the tonearm movements and the related noise can be viewed in the same time scale.
This audio-video comparison is shown in Att.1. We see the alterations of the tonearm horizontal position, that of the tonearm horizontal velocity and the noise waveform in the same time scale 0 - 5 sec. The horizontal velocity view allows to select a velocity region for the noise level measurements, while the horizontal position view allows a rough evaluation of the decay constant and hence - the evaluation of the friction coefficient.
All the noise levels in Att.1. refer to my own "reference level" - that of the highest peaks I observe in my LP recordings. Expressed in cm/s value, my "0 dB" corresponds to about 20 cm/s or 4 x the reference 5 cm/s level. So, to compare my values with some others, based on 5 cm/s 0 dB level, one has to increase them by 12 dB.
Given the above clarifications, I measure in the 'typical' 1 mm/s velocity level tonearm noise maxima of -83 dB in my reference scale and -71 dB in the "0 - 5 cm/s" scale.
All the RMS values are unweighted. If I weight them according to ITU-R 468, the noise values approach -100 dB "PK" or -88 dB "5 cm/s".
I will post later the analysis of the oscillations decay, which indicate a friction coefficient about 50 dyne/(cm/s) or a force of 5 dyne for a velocity of 1 mm/s. 1 mm/s is close to the maximum horizontal velocity of the stylus in the case of a 0.3 mm groove eccentricity.
Eora 3 75 g.mp4 - Google Drive
The new swing has the same length of 33 cm, but 43 g are added to the swing base, so that the total moving mass rises to 75 g. This results in longer durations of the visible decaying oscillations. The friction force is not affected by the rise of the mass. The video is now taken with my digital microscope camera and allows higher measuring precision, of the order of 0.03 mm. I include a link to the microscope video. Another new feature is the parallel video and audio recording, so that the tonearm movements and the related noise can be viewed in the same time scale.
This audio-video comparison is shown in Att.1. We see the alterations of the tonearm horizontal position, that of the tonearm horizontal velocity and the noise waveform in the same time scale 0 - 5 sec. The horizontal velocity view allows to select a velocity region for the noise level measurements, while the horizontal position view allows a rough evaluation of the decay constant and hence - the evaluation of the friction coefficient.
All the noise levels in Att.1. refer to my own "reference level" - that of the highest peaks I observe in my LP recordings. Expressed in cm/s value, my "0 dB" corresponds to about 20 cm/s or 4 x the reference 5 cm/s level. So, to compare my values with some others, based on 5 cm/s 0 dB level, one has to increase them by 12 dB.
Given the above clarifications, I measure in the 'typical' 1 mm/s velocity level tonearm noise maxima of -83 dB in my reference scale and -71 dB in the "0 - 5 cm/s" scale.
All the RMS values are unweighted. If I weight them according to ITU-R 468, the noise values approach -100 dB "PK" or -88 dB "5 cm/s".
I will post later the analysis of the oscillations decay, which indicate a friction coefficient about 50 dyne/(cm/s) or a force of 5 dyne for a velocity of 1 mm/s. 1 mm/s is close to the maximum horizontal velocity of the stylus in the case of a 0.3 mm groove eccentricity.
Eora 3 75 g.mp4 - Google Drive
Attachments
Last edited:
Member
Joined 2019
The Eora 3 velocity analysis
I take 2 velocity regions and calculate the deceleration of the velocity maxima within each one. The calculations indicate a best friction function fit of the type
F(friction) in dyne = 53 V in cm/s
For my 'standard' 1 mm/s velocity (which is close to the 0.3 mm 33.3 rpm eccentricity maximum velocity) the function indicates a friction force of 5.3 dyne, which I consider as a very good value.
This is an 'approximative' method, but I estimate it's error as < 10%.
I take 2 velocity regions and calculate the deceleration of the velocity maxima within each one. The calculations indicate a best friction function fit of the type
F(friction) in dyne = 53 V in cm/s
For my 'standard' 1 mm/s velocity (which is close to the 0.3 mm 33.3 rpm eccentricity maximum velocity) the function indicates a friction force of 5.3 dyne, which I consider as a very good value.
This is an 'approximative' method, but I estimate it's error as < 10%.
Attachments
Last edited:
Member
Joined 2019
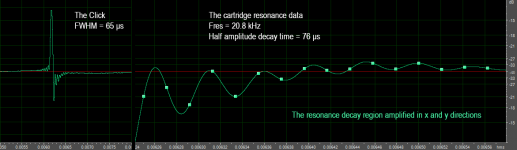
The "Good Clicks" Measurements
A click is "good" when it is very short and moderately high. These clicks are quite close in form to a very short single triangular pulse. They are also "good" from the Clicks Removal point of view: they are easily recognizable and reparable with a very low rate of false detection. Contrary to the "pops", which are a sort of very bad clicks by all means.
I selected a click of nearly 100 μs duration, with FWHM = 65 μs. The decay of the oscillations following this click provides us with information about:
1. The high frequency resonance of the cartridge.
2. The decay rate of this resonance.
The data are presented in the attachment. They refer to AT95EX cartridge in my TTT tonearm playing a normal quality LP.
A click is "good" when it is very short and moderately high. These clicks are quite close in form to a very short single triangular pulse. They are also "good" from the Clicks Removal point of view: they are easily recognizable and reparable with a very low rate of false detection. Contrary to the "pops", which are a sort of very bad clicks by all means.
I selected a click of nearly 100 μs duration, with FWHM = 65 μs. The decay of the oscillations following this click provides us with information about:
1. The high frequency resonance of the cartridge.
2. The decay rate of this resonance.
The data are presented in the attachment. They refer to AT95EX cartridge in my TTT tonearm playing a normal quality LP.
Attachments
Last edited:
Member
Joined 2019
Test recording in OGG highest quality variable bitrate format. In the most demanding parts the bitrate may reach and even exceed 500 kbps. The OGG versions of my YouTube clips are made for use by my Facebook friends. They are deleted after 1 month.
Liszt
Hungarian Rhapsodies No 4, 5, 6 and 7
Hungaroton LPX 11488 B
Hungary, (unknown year of release)
00:00 Rhapsody No 4. Piano - Gabriella Torma
05:01 Rhapsody No 5. Piano - Gabriella Torma
13:48 Rhapsody No 6. Piano - Gábor Gabos
20:58 Rhapsody No 7. Piano - Erika Lux
26:42 End of file
The OGG file:
Liszt Hungarian Rhapsodies No 4 5 6 7.ogg - Google Drive
The permanent YouTube file:
YouTube
Liszt
Hungarian Rhapsodies No 4, 5, 6 and 7
Hungaroton LPX 11488 B
Hungary, (unknown year of release)
00:00 Rhapsody No 4. Piano - Gabriella Torma
05:01 Rhapsody No 5. Piano - Gabriella Torma
13:48 Rhapsody No 6. Piano - Gábor Gabos
20:58 Rhapsody No 7. Piano - Erika Lux
26:42 End of file
The OGG file:
Liszt Hungarian Rhapsodies No 4 5 6 7.ogg - Google Drive
The permanent YouTube file:
YouTube
Member
Joined 2019
The year of release is 1971.
Köszönöm! I can not change the clip picture, but I will change the Notes text.
Member
Joined 2019
Ferenc Liszt
Hungarian Rhapsody No14
Hungaroton LPX 11490 A
Hungary, 1971
Piano - Gabriella Torma
Recorded with TTT turntable.
Edited with my standard procedures.
Liszt Hungarian Rhapsody No14.flac - Google Drive
Hungarian Rhapsody No14
Hungaroton LPX 11490 A
Hungary, 1971
Piano - Gabriella Torma
Recorded with TTT turntable.
Edited with my standard procedures.
Liszt Hungarian Rhapsody No14.flac - Google Drive
Member
Joined 2019
TTT test recording after certain modifications:
- New, harder test boat
- New leading wheels bearings
- 25 Hz FFT rumble cut
- Lighter Brian Davies clicks removal
Erroll Garner - Jazz Portrait
AMIGA 8 55 205, DDR, 1980
Octave Records Inc. , 1965
Metro-Goldwyn-Mayer Inc., New York, USA
YouTube
Since 1 month my YouTube clips are available also in webm format, where the sound part is encoded in Opus audio.
- New, harder test boat
- New leading wheels bearings
- 25 Hz FFT rumble cut
- Lighter Brian Davies clicks removal
Erroll Garner - Jazz Portrait
AMIGA 8 55 205, DDR, 1980
Octave Records Inc. , 1965
Metro-Goldwyn-Mayer Inc., New York, USA
YouTube
Since 1 month my YouTube clips are available also in webm format, where the sound part is encoded in Opus audio.
A click is "good" when it is very short and moderately high. These clicks are quite close in form to a very short single triangular pulse.
How does the cartridge know to resonate before the click?
Member
Joined 2019
How does the cartridge know to resonate before the click?
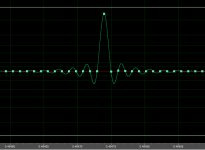
The cartridge can not know, so it is something else.. Let me guess.. Aha! This is a way of Adobe Audition presentation..? Let me try an artificial click, a DIY one. No cartridge. And still, something before and after the peak … With the quantization frequency / 2 (Att.1).
In my click there is a strong asymmetry, so I believe that part of the right side oscillations 'describe' some decaying resonance. The frequency there is NOT the quantization one / 2 = 24 kHz.
An example of an actual click with a very weak "cartridge prediction" is given in Att.2. Here the recording quantization is 96 kHz.
Attachments
Last edited:
Member
Joined 2019
How does the perpetrator consider these resent acts?
Cheers!
I do not understand your question. But I understand the "Cheers!"

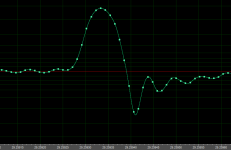
Dr. Kritidis, the left picture above appears to be the impulse response of a digital filter somewhere in the processing chain.
Member
Joined 2019
Dr. Kritidis, the left picture above appears to be the impulse response of a digital filter somewhere in the processing chain.
This is the way Adobe Audition presents a single quantum peak. No processing. Only 2 steps:
1. Generate silence.
2. Change (by hand) a single value from abs. 0 to something near 0 dB.
Last edited:
Member
Joined 2019
No processing.
I meant "no processing by my side". Clearly the way Adobe Audition presents the waveform in high time amplification.
Last edited:
Audition displays a virtual sinc reconstruction of the waveform. The Gibbs effect "ringing" is what you see.
I do not understand your question. But I understand the "Cheers!"
I meant; What do you think about the change to new boat and bearing? 🙂
Cheers!
Member
Joined 2019
The Gibbs effect "ringing" is what you see.
I keep silence expecting some continuation. Because in my #192 I wrote about after-clicks ringing with frequency different from Fquant/2. In Attechment 2 - a really recorded click - the ringing F is close to 20 kHz - much lower than the 48 kHz of my "model click" in Attechment 1.
Last edited:
Member
Joined 2019
I meant; What do you think about the change to new boat and bearing?
Well, the new boat is quite better in the sense than new fine adjustments of the floating balance have been added: for the directions left-right and front-back. It is still an object under development.
As for the bearings, I did not make yet the "big step" of using a much finer and expensive ones. I just made a standard procedure for measuring of the bearings torque, applied it to all my existing pieces and selected the pair with lower values.
I made also a new type of measurements of the tonearm rolling noise, which I will describe later today.
Regards.
- Home
- Source & Line
- Analogue Source
- Floating Tangential Tonearm