Bob Cordell said:
OK, I wasn't actually implying that you were under the misconception. It's was obvious from your post that you are not. I was simply elaborating a bit further the point. Glad you agree.
Cheers,
Glen
G.Kleinschmidt said:
You might be surprised at the result. If one assumes noiseless feedback resistors, the equivalent input noise of an amplifier is the same with and without feedback. Output noise of a feedback amplifier with the feedback disabled is not meaningful, because the equivalent input noise is being multiplied by the open-loop gain.
Have a look at this book. In the search box, enter "feedback" without quotes. Then click item number 2 (where it says "On Page 54") to read the chapter.
The site is asking me for registration when I perform the last of the actions you listed. Why don't you post the relevant text here and save us the trouble?
It's a whole chapter of a book.
Try looking up "Low Noise Electronic System Design" on Amazon. Then click on "search inside" and try it. Hopefully that will work without registration.
I'm guessing the registration might be because my link may have pointed to the U.S. Amazon site and you're not in the U.S.
Try looking up "Low Noise Electronic System Design" on Amazon. Then click on "search inside" and try it. Hopefully that will work without registration.
I'm guessing the registration might be because my link may have pointed to the U.S. Amazon site and you're not in the U.S.
andy_c said:
I can access it from Europe but then I am a registered customer with Amazone US, maybe that's the point.
Jan Didden
janneman said:
Jan, I agree, we should forget about the 67k resistor for now.
I don't completely agree with your reasoning, at least as you stated it. We certainly want the most linear open loop amplifier possible before we apply feedback. There is no controversy there.
First, however, in a feedback situation, we have to be careful in how we view open loop nonlinearity. This is subtle, and I will probably not do a perfect job in explaining it. For purposes of the final outcome in a feedback situation, a very lightly loaded VAS that has high gain and a bit of open loop nonlinearity due to some nonlinearity in the light load is no more linear than that same VAS loaded with a load resistor which reduces the open loop gain and makes a reduction in its open loop distortion. This is because the increase in linearity is only apparent, it is not fundamental. The increased feedback when the resistor is not present will reduce that nonlinearity to the same level in the closed loop as if the resistor was there. The root of the open loop nonlinearity, the nonlinearity in the light loading, has not changed.
If you think in terms of input-referred distortion, just as you do with input-referred noise, you will see the point. Indeed, the concept of input-referred distortion analysis, which effectively breaks the feedback loop, is a very important analysis tool. Input-referred distortion analysis means that you assume a perfect output signal and then calculate what amount of distortion is necessary in the input signal to produce that perfect output signal in light of the intervening nonlinearities.
The other thing which I think you are touching on is re-entrant distortion with negative feedback. This refers to the distortion in the feedback again mixing with the input signal in the forward path nonlinearities. If, for example, you had a forward path that created only pure second harmonic distortion, the second harmonic appearing in the output would feedback and mix with the input signal and in going through the forward path would then create third harmonic distortion.
Re-entrant distortion is a real phenomenon, but one has to carefully analyze it and put numbers on it. Input referred distortion analysis is a powerful tool in this regard. It turns out that if you plot the strength of the re-entrant distortion effect, you will see that it starts out at zero with no negative feedback, then increases as negative feedback is applied and increased, and then begins to decrease as NFB is further increased. Somewhere around 10 dB of feedback is where it is worst. Hood or Baxendal showed this a long time ago. This also could be construed to suggest that, if you are going to have negative feedback, you are best off to have at least 20 dB of negative feedback.
The point here is that increasing amounts of negative feedback beyond that 10 dB number or so does NOT increase the buildup of higher-order nonlinearities. But keep in mind that this does not change the important goal of having the most linear forward path in the first place.
Cheers,
Bob
G.Kleinschmidt said:
Its just noise theory in relation to negative feedback. You need to look at that more closely. Looking at the noise of an open loop amplifier is not a good experiment in this context. You need to think in terms of input-referred noise.
Many people think that the achievement of high dc open loop gain is something that people like myself strive for. That is wrong. I really don't care whether the open loop gain is 100 dB or 180 dB. It is what it is. It is high only as a consequence of the circuit design features that I have incorporated to make the forward path fast and linear. I didn't TRY to make it that high. Things like emitter follower buffers between stages for isolation and things like current mirror loads tend to make the d.c. open loop gain high.
Many of those same people also don't realise that the open loop gain in such cases is very high at d.c., but not necessarily really high in the audio band. They also don't realise that the compensation (such as Miller compensation) is really in control of that gain, even down to subsonic frequencies. Just extrapolate back at 6 dB per octave from the amount of NFB you have at 20 kHz, and you'll see how much OLG you have under compensated conditions down to very low frequencies. The OLG will tend to keep rising as frequency decreases until it reaches the value of the dc OLG. It is very simple.
Cheers,
Bob
G.Kleinschmidt said:
Hi Glen, I did not miss your point. I was disagreeing with something you said in making that point (namely that the loading of the compensation capacitor on the VAS at frequencies above 20 kHz could make it work harder and be a problem).
I think we have been in agreement with regard to the relative insignificance of the 67k resistor at high frequencies, and I don't even remember who brought it up.
We have not been in agreement in regard to your suggestion that its presence has value at low frequencies. It has no value at low frequencies.
Cheers,
Bob
andy_c said:
I disagree. I haven't read your reference yet (I need to sign up as member at Amazon), but I believe that my OL results are meaningful because they demonstrate the fact that the junction noise of the BJT differential input amplifier is greater than the differential voltage that would be required to drive the output to the required level, closed loop or not. The noise test was specifically performed with the bases of the input transistors tied directly to ground. The DC servo stabilises the DC operating point of the amplifier by acting upon the Ic balance of the secondary cascaded differential amplifier. Incidentally, I’m using transistors with fT’s in the 0.8-1.2GHz range.
I have a book (now out of print) with a chapter on noise that discusses with a bit of depth the relationship and limitations between very high OLG and noise generation in op-amp design, when the OLG gain becomes so high that the amplitude of the closed loop error signal approaches the input stage generated noise. Essentially, a section of a chapter articulating somewhat better the issue I have been discussing here. If you are happy to provide an email address, I’d be happy to scan it and email it to you.
Cheers,
Glen
Bob Cordell said:
I did not say and am not of the opinion that the 67k resistor has value at low frequencies. I am of the opinion that limiting OLG can have value in terms of noise under specific conditions. Lightly resistively loading the VAS can achieve this.
This discussion is starting to go around in circles. The amplifier I am prototyping, and the design goals have very little in common with your 50W MOSFET power amplifier. The fT’s of the transistors (being RF types) are much greater and so is the compensation crossover frequency, as well as the compensated gain at 20kHz, with the compensation scheme no being simple miller compensation.
When both the bandwidth and the OLG are as high, the noise performance is compromised by other circuit limitations, one being the junction noise generated in the input devices, and this limitation has a relationship to the OLG.
To repeat what I’ve already posted to Andy, :
I have a book (now out of print) with a chapter on noise that discusses with a bit of depth the relationship and limitations between very high OLG and noise generation in op-amp design, when the OLG gain becomes so high that the amplitude of the closed loop error signal approaches the input stage generated noise. Essentially, a section of a chapter articulating somewhat better the issue I have been discussing here. If you are happy to provide an email address, I’d be happy to scan it and email it to you.
Cheers,
Glen
I got interested in 2 things :
1. Miller cap actually takes gain at high frequencies (in the sake of stability), where actually this gain at high frequenies is needed to fix linearity at high frequencies (by feedback).
2. Having OL gain as big as possible (ie : error signal as small as possible at input differential) possibly has its limit, when the error signal is comparable to noise of the differential transistor
What should a good amp design looks like ? 😀
1. Miller cap actually takes gain at high frequencies (in the sake of stability), where actually this gain at high frequenies is needed to fix linearity at high frequencies (by feedback).
2. Having OL gain as big as possible (ie : error signal as small as possible at input differential) possibly has its limit, when the error signal is comparable to noise of the differential transistor
What should a good amp design looks like ? 😀
G.Kleinschmidt said:
Glen,
You're right about one thing: this discussion is going around in circles.
Tell us the title and author of the book. Just because something is written in a book does not make it right. If what you were saying had merit, the concept and point would be made in plenty of books that are still in print.
The concept that open loop gain that is so high at low frequencies that the error signal must be smaller than the input-referred noise of the input stage seems nicely intuitive, but it is simply wrong.
Tell us more about this mysterious amplifier of yours. What is the gain crossover frequency? What is the compensation rolloff rate? What kind of compensation are you using if it is not Miller. I told you about mine, why don't you elaborate on yours.
Cheers,
Bob
Bob Cordell said:
If it is assumed that by ''complementary VAS'' you are referring to the second stage in your design here, then your supposition that it would necessarily require two miller capacitors for compensation is incorrect: only one is required.
Bob Cordell said:
''worry.....needlessly'' is right.
Bob Cordell said:
Not necessarily true either. One needs to define with precision what one means by ''sub-optimal slew rate'' and in what context the phrase is applied.
Bob Cordell said:
Not true. Your feedback compensation is actually phase lead compensation. Completely unrelated to Miller-type compensation in theory and in fact.
Moreover, this sort of compensation must, of necessity, be augmented by shunt and/or miller compensation if adequate stability margins are to obtained with your design.
Finally, see:
http://www.diyaudio.com/forums/showthread.php?s=&postid=1047674&highlight=#post1047674
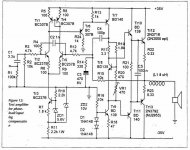
In a paper (by John Ellis P.hd), he proposed PLIL (Phase Lead Input Lag) method as an alternative method to stabilize an amp without Miller cap.
Phase lead = C4
Input lag = R4+C2
These 2 must both be used together.
Notice also he put R3 and R12.
In Bob's amp, the RC network in differential is put between collectors of input differential, in John Ellis' it is put on bases of input differential.
Phase lead = C4
Input lag = R4+C2
These 2 must both be used together.
Notice also he put R3 and R12.
In Bob's amp, the RC network in differential is put between collectors of input differential, in John Ellis' it is put on bases of input differential.
Attachments
J Ellis schematic
Hi,
what is the purpose of r12?
or is it simply to balance the input conditions with r3?
Note r17, compensation for constant voltage as Iq of the ccs (tr9) varies. Same as D. Self discusses but much later.
Hi,
what is the purpose of r12?
or is it simply to balance the input conditions with r3?
Note r17, compensation for constant voltage as Iq of the ccs (tr9) varies. Same as D. Self discusses but much later.
Hi, Mikeks,
PLIL has 2 components that must be used together "PL"and "IL".
If you only use C4, you don't make "PLIL", just "phase lead" compensation. John Ellis found out that only using "PL" is not enough to make an amp stable.
"PL" can be accompanied by (smaller) miller cap to make an amp stabile, but here it is the miller cap that is tried to be eliminated.
So "PL" needs another accompany to make the amp stable, but what? J. Ellis suggest to use "IL" to accompany "PL". The overall bode plot result of PLIL looks nice, but each component value of PLIL needs to be calculated.
PLIL has 2 components that must be used together "PL"and "IL".
If you only use C4, you don't make "PLIL", just "phase lead" compensation. John Ellis found out that only using "PL" is not enough to make an amp stable.
"PL" can be accompanied by (smaller) miller cap to make an amp stabile, but here it is the miller cap that is tried to be eliminated.
So "PL" needs another accompany to make the amp stable, but what? J. Ellis suggest to use "IL" to accompany "PL". The overall bode plot result of PLIL looks nice, but each component value of PLIL needs to be calculated.
Attachments
