janneman said:
In my lingo, HEC is a subset of GNFB topologies. So I'd like to restate your question as the different approach when using a PFB to generate excess forward gain as opposed to a miller VAS.
Rodolfo knows better than I. With PFB you don't have to design the gain as it comes out in the wash. But you do have to worry about the bandwidth and the linearity of the summer. With miller you have to design the gain in and then limit the bandwidth with a capacitor.
So I think I agree.
janneman said:
Hi Jan,
All of these imperfection arguments and realities of finite bandwidth largely apply to feedforward as well, although in slightly different forms.
I would say that even if we could build a summer with infinite bandwidth we would still not have perfect HEC as long as we still had an output stage with finite bandwidth and excess phase.
Cheers,
Bob
Bob Cordell said:
Interestingly and just to complement, the limitation does not come per se from the output stage bandwidth or phase shift.
In theory, only the performance of the summing node determines the accuracy of correction - this comes out readily from the algebra when you evaluate sensitiviy.
The actual limitation is in the fact that stability most of the time goes through the roof, though I have not seen it proved in a generalized form.
Rodolfo
My hint - no formal proof - with respect to the last comment, comes from the fact that given any nonzero amount of phase shift in the output stage, then increasing bandwidth in the summing node which translates to increasing gain, translates sooner or later to higher than unity gain positive feedback above certain frequency, but in reality things are more complex.
Rodolfo
Rodolfo
Bob Cordell said:
Yes. The limitation is one of compound phase shift in all elements around the NFB loop. So summer bandwidth and plant bandwidth and other components all limit the amount of stable loop gain that can be applied. Of course, this is exactly the same issue with any NFB topology.
So I think a useful question to discuss may be whether the servo topology with PFB loop is an inherently better feedback network in respect of bandwidth and linearity than conventional topologies, like Miller.
But I think your point, Bob, is that ultimately the plant will be self-limiting because in power transistor applications like we are talking about, the plant will always be the slowest and least linear element in the loop.
Brian
ingrast said:
That's right. you can only have stable, infinite FB if all elements in the FB loop have zero phase shift at all frequencies. A tall order!
ingrast said:
Hi Rodolfo,
Of course. If the summing nodes are capable to reduce harmonic distortion, they also are capable to reduce all other kind of distortions, like non-harmonic, phase shift, etc.
Regards,
Edmond.
traderbam said:
The crux of the matter as in any regular NFB scheme - mostly Control Systems Theory is about this - is to satisfy Nyquist stability criterion as per linear time invariant systems plus the nasty reality that no actual system is linear and time invariant at all.
So sometimes clever compensation may save the day or better said, push the limits further up. I concur in this respect EC and NFB deal in the end with the same beast, the difference being the means of getting gain.
Rodolfo
traderbam said:
Hi Brian,
Well stated.
Moreover, I agree that as long as HEC can be viewed as NFB with a PFB inside that gives theoretically infinite gain at DC, then it is a fair question whether HEC has advantages over a more conventional NFB arrangement like Miller. BTW, I prefer the term NFB to servo, but this is just a nit.
Although some will agree or not to the validity and/or value of the other views of HEC, I certainly agree that the NFB view of HEC is valid as long as it is applied correctly.
I do also believe that the power transistors are largely the main limitation to HEC performance, so in rough terms, the higher the ft the more improvement one is likely able to get out of HEC or any form of local NFB placed around the output stage.
I believe that one topological advantage of the HEC architecture is that the way that the main compensation can be applied to HEC is effectively bypassing the differencing stage, perhaps providing less opportunity for excess phase to enter the picture.
Some of the critical small-signal transistors in HEC operate at fairly low voltages, so it may be easier to employ devices with ft in the GHz range in those locations.
Cheers,
Bob
Hi,
No Sir, not all kinds of distortions. This mechanism introduces distortions also, like phase distortion.
Exactly, therefore, it works in simulation only.
Bob Cordell said:
In the meantime I was playing with my simulator and the results confirm that even if we have summers/subtractors with infinite BW and zero phase shift, we cannot build a perfect HEC. The phase shift of the OPS is a limiting factor as well. If it reaches -360 degrees we get in trouble.
The circuit below, for example, gets unstable if S1>0.975. Below this critical value the THD20 sticks at an unexciting 65ppm.
But now comes a surprise: If I inserted an additional roll-off between S1 and S2, the max. allowed gain of S1 is very close to 1 (but not exactly 1). Consequently, the THD20 figure is much better: 13ppm
BTW1, the unity loop gain frequency seen at point C is 10MHz (and probably too high for a real circuit).
BTW2, 13ppm isn't the best we can get. A similar OPS based on GNF+TMC gives a 10 times better THD figure.
Anyhow, my previous remark that perfect summers can correct all phase shifts of an OPS, was plain BS.
Regards,
Edmond
edit: S1 > is also allowed.
Attachments
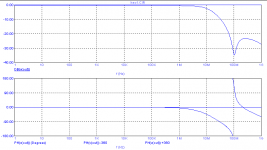
Edmond,
Do you perchance have a gain vs freq curve of the output stage alone, iow where are the poles & zero's?
Jan Didden
Do you perchance have a gain vs freq curve of the output stage alone, iow where are the poles & zero's?
Jan Didden
Edmond Stuart said:
In the meantime I was playing with my simulator and the results confirm that even if we have summers/subtractors with infinite BW and zero phase shift, we cannot build a perfect HEC. The phase shift of the OPS is a limiting factor as well. If it reaches -360 degrees we get in trouble.
To state the obvious, in a FB control system (as opposed to a additive correction system like pre-distortion or feed-forward), the distortion reduction will be a function of both error sense accuracy (summer accuracy) and stability of the control loop. Forget either one of these at your peril!
So the plants phase shift always limits the maximum error correction achievable, even if you have perfect FB network components. The higher the (phase) bandwidth of the plant, for a given amount of non-linearity, the lower the corrected distortion can be.
QED 😀
PS: post 3653 contains an error 'S1 > is also allowed' should be: 'S1 > 1 is also allowed.'
PS: post 3653 contains an error 'S1 > is also allowed' should be: 'S1 > 1 is also allowed.'
traderbam said:
To state the obvious, in a FB control system (as opposed to a additive correction system like pre-distortion or feed-forward), the distortion reduction will be a function of both error sense accuracy (summer accuracy) and stability of the control loop. Forget either one of these at your peril!
So the plants phase shift always limits the maximum error correction achievable, even if you have perfect FB network components. The higher the (phase) bandwidth of the plant, for a given amount of non-linearity, the lower the corrected distortion can be.
Yes, with the caveat that you can almost arbitrarily correct the errors if they appear at lower frequencies. Like in the limiting case at f=0 (DC) you can correct perfectly. That's not a practical use, I concede that.
What I found is that you get the 'nicest' cl response (peaking only 3dB at hf) if you keep the ratio of the BW of the summers and the plant at 1.
Jan Didden