Surely just dropping a large cap on the o/p of a reg can result in resonance with the inductive o/p Z of the reg unless it's well damped with a small resistor, which would inevitably increase o/p Z.
JBAU SEEMS TO HAVE GOT IT RIGHT SINCE THE PHASE IS UNIFORM, BUT HE NEEDS TO SPECIFY THE TYPE OF OUTPUT CAP HE USES AND/OR ITS ESR FOR THIS RESULT TO BE REPRODUCIBLE FOR OTHER USERS.
JBAU SEEMS TO HAVE GOT IT RIGHT SINCE THE PHASE IS UNIFORM, BUT HE NEEDS TO SPECIFY THE TYPE OF OUTPUT CAP HE USES AND/OR ITS ESR FOR THIS RESULT TO BE REPRODUCIBLE FOR OTHER USERS.
okapi's explanation is essentially correct. The paralleled output caps dominate at higher freq's, until their reactance starts trending toward inductive and the whole Z picture becomes much messier.Gopher said:
Gopher said:
Yes, they both are. As I had stated, the optimisation objective is "low, linear, and matched." The first one is the best match to the LM317, the second is best match to the LT1085.
I may have declared finality too soon. In last night's experiment: By using an additional RC across the adjust cap to shape the whole spectrum, I can lower the linear-Z region down to the 18milliOhm zone over a broader range on both regs, with even flatter phase up to 5kHz. But then the phase breaks upward a bit more quickly than before. I'm not a fan of sharp phase transitions, but a 25% reduction in output Z over most of the audio range is nothing to snarf at. I'll be working on this more today.
I think I see what you are getting at in the bigger picture, Gopher. There are definite interactions between the downward-sloping error amp curve, gain factors controlled by the adjust pin current, the reactance from adjust to ground, and the output caps. The error amp curve is fixed: the others we can tweak. So those are the factors I've been trying to balance for best performance in the audio range.
On the LM317, the critical interaction zone is in the 500-600Hz region. On the LT1085, it is in the 2-3KHz range. You can see the broad bump there. That bump, with the dip that follows, is the warning sign of potential instability and resonance. You can bring that resonance out more by increasing the adjust pin current.
The output caps: In order make easy changes, I have five caps on the fixture and connect them as needed: 1000uF/35V and 470uF/50V lytics, 5.6uF, 4.7uF, and 100nF films. The lytics are good quality but nothing special ESR-wise. I haven't found it to be that critical. Maybe at higher freq's it would play more of a role.
On the LM317, the critical interaction zone is in the 500-600Hz region. On the LT1085, it is in the 2-3KHz range. You can see the broad bump there. That bump, with the dip that follows, is the warning sign of potential instability and resonance. You can bring that resonance out more by increasing the adjust pin current.
The output caps: In order make easy changes, I have five caps on the fixture and connect them as needed: 1000uF/35V and 470uF/50V lytics, 5.6uF, 4.7uF, and 100nF films. The lytics are good quality but nothing special ESR-wise. I haven't found it to be that critical. Maybe at higher freq's it would play more of a role.
soongsc,
I have done no simulations (beyond the usual mental math...) These are all actual measurements, made with an HP 4276A LCZ Meter. The data is gathered via GPIB and plotted by computer. The 4276A has features that allow it to make in-circuit measurements of DC-biased, grounded devices that many LCR meters can not do. Most important is the transformer coupling of the oscillator to the DUT, which isolates the DC component. If you try this with a different meter, first study it's input circuitry to make sure it is safe. Otherwise you'll have an expensive repair bill on your hands...
Your comment about snubbers is interesting. I plan on trying some snubber-like input filters with the 5V regs, partly because there is so much input voltage to play with, and these regs all work better with low Vin-Vout. So maybe we can use some of it to clean up the noise, without causing other problems. We shall see...
I have done no simulations (beyond the usual mental math...) These are all actual measurements, made with an HP 4276A LCZ Meter. The data is gathered via GPIB and plotted by computer. The 4276A has features that allow it to make in-circuit measurements of DC-biased, grounded devices that many LCR meters can not do. Most important is the transformer coupling of the oscillator to the DUT, which isolates the DC component. If you try this with a different meter, first study it's input circuitry to make sure it is safe. Otherwise you'll have an expensive repair bill on your hands...
Your comment about snubbers is interesting. I plan on trying some snubber-like input filters with the 5V regs, partly because there is so much input voltage to play with, and these regs all work better with low Vin-Vout. So maybe we can use some of it to clean up the noise, without causing other problems. We shall see...
jbau said:
I'd like to make sure I'm on the same page here. You are measuring the phase angle between two quantities: the voltage drop across the load (V_out), and the current through the load (I_load). The regulator, by definition, tries to keep Vout constant at some set value, in spite of two factors: 1) voltage variation that comes from the line side, and voltage variation induced by the varying current drawn by the load, I_load. The regulator response to 1) is what we call line regulation, and it's response to 2) we call load regulation. The important fact here is that the end result is the constant voltage V_out. We also know that in the real world absolutes don't really exist, so V_out is not so constant; it will have an AC component. My earlier point was that if this AC component is so small as to not possibly be audible, then the load is presented with (as far as audibility is concerned), a "constant" voltage. Close enough to DC that we would not hear de difference. So my point was, if this was the case, then the phase angle between this AC component of V_out and I_load is not of any consequence. To simplify the analysis let's assume that line regulation is very good and no ripple on V_out is due to the input voltage. Then any ripple on V_out can only be induced by variations in I_load in conjunction with Z_out. IF Z_out is very small even in the higher frequency range, then it follows that the ripple on V_out is very small, as to no longer matter what the phase shift is.
Now, realistically, we cannot assume that Z_out is really that small. Then what about the phase angle between I_load and V_out? Well, if it is small, this mean that the regulator responds very quickly to a change in I_load. Would mean that a high slew rate is a desirable criterion? Whatever we call it, high slew rate, small phase shift, the actual mechanism it describes is the speed of response of the regulator in adjusting "whatever" so that V_out gets closer to some constant ideal, when I_load varies (suddenly or otherwise).
BTW I have read the document you pointed to. Can you please (for my own curiosity and education) describe the Z_out/phase measurement setup that you are using for these results?
And, for the record, I'm talking in the interest of getting good results. No criticism or attacks intended. I come in peace
iko, thanks for the questions. No worries, no criticism taken.
The only way to test the Z/phase is to push AC into it and measure the outcome. What we now measure as complex load impedance becomes the source impedance to the circuit it is feeding. Current is delivered to it through that Z/phase profile.
I've never tested this theory directly, but it makes sense to me that circuits without negative feedback would benefit more from linear Z/phase supplies than would NFB devices. NFB devices will swamp some of the effects. We see this in the symmetry error measurements, where the result was trumped by the available gain for feedback. So I'm really looking forward to seeing how well this works with A/D converters.
I think I answered that in response to soongsc's question. I should add, the 4276A doesn't actually "compute" the phase with math; it does it in hardware, using zero-crossing detectors in the voltage and current channels, measures their time difference, and then normalizes that to the frequency period for the phase figure.
Hope this helps.
I think this is the point of divergence. I see that as the lesser of two important facts. The other is that current be supplied as and when demanded. For example, let's say the circuit is demanding 1 milliamp peak now for a cosine pulse, it will draw that regardless of the voltage limits, as long as the circuit is not clipping. That's why I refer to these voltage supplies as "current pipes" or "constant-voltage/current-on-demand." Put a current probe on the supply leads (or, better, the ground return) and monitor it on your scope next to the input signal to the circuit that the supply is feeding, and you'll see that's where all the action is. The supply voltage ripple caused by the current modulating the finite output impedance is important (more important for some devices than for others), but is small potatoes compared to the importance of the fidelity and timing of the current waveform. So the difference is mainly one of emphasis. The voltage(s) set the operating range in which current is delivered.
The only way to test the Z/phase is to push AC into it and measure the outcome. What we now measure as complex load impedance becomes the source impedance to the circuit it is feeding. Current is delivered to it through that Z/phase profile.
I've never tested this theory directly, but it makes sense to me that circuits without negative feedback would benefit more from linear Z/phase supplies than would NFB devices. NFB devices will swamp some of the effects. We see this in the symmetry error measurements, where the result was trumped by the available gain for feedback. So I'm really looking forward to seeing how well this works with A/D converters.
I think I answered that in response to soongsc's question. I should add, the 4276A doesn't actually "compute" the phase with math; it does it in hardware, using zero-crossing detectors in the voltage and current channels, measures their time difference, and then normalizes that to the frequency period for the phase figure.
Hope this helps.
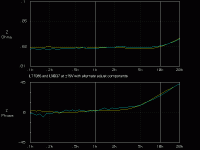
Here is an alternative, using an additional RC across the adjust cap to "shape" the overall impedance slope while optimizing the adjust cap. Everything is the same as previous, except change the adjust to ground components to this:
The resulting Z/phase curve is below. Now if you didn't see the phase curve, this would look like a definite improvement over the simpler version. The mean impedance value is around 19 milliOhms vs 24 for the previous. And the Z curve is quite flat up to 10kHz. But the phase departure is quite a bit worse. Wringing out that lower Z comes at a cost.
Anyway, do with this what you will. If you don't think phase is important, but like the idea of a flatter Z over a wider range, then this one's for you. It's still better than what the factory recommends.
One of the units I'm modding needs ±12 VDC so I'm going to cook up one of those next.
Code:
LM337:
a 6.8uF 2.04k
d /----||----/\/\/\----\ gnd
j \--------||----------/
68nF
LT1085:
a 680nF 5.1k
d /----||----/\/\/\----\ gnd
j \--------||----------/
120nFAnyway, do with this what you will. If you don't think phase is important, but like the idea of a flatter Z over a wider range, then this one's for you. It's still better than what the factory recommends.
One of the units I'm modding needs ±12 VDC so I'm going to cook up one of those next.
Attachments
jbau said:
I don't disagree; I just see the two facts interconnected, not separately. You know what happens when a large current is drawn from an unregulated and weak power supply: the voltage sags. Only if the supply can provide the needed current as demanded will the voltage not sag.
The magnitude of the phase angle between the drawn load current and the output voltage (which I agree, sets the operating point) will be directly related to the speed with which the regulator responds, if it is capable to respond adequately (delivering the needed current). In other words, when the current is demanded by the load, the magnitude of the impedance will determine how that "quantity" of current can be delivered, and the magnitude of the phase shift describes how timely that current was delivered. (I'm just thinking aloud here.) This is roughly how I see the importance of the phase angle.
OK, thanks, that makes a little more sense. Not so clear how the dynamic load is implemented; also it would be nice to get some idea about the values seen when testing, like X mA DC with a Y mA AC component (load current) induces an AC component of Z mV. Perhaps you've already described this in an earlier post? If so, please just say yes and I'll look back in the thread. Sorry if I seem such a pest, but sometimes I find it best to have things spelled out pretty clearly. Too often I see full blown polemics because things are described at too high a level and there's too much room left for interpretation.
I looked back in the thread and realized that your interest is in small three terminal regulators because of space concerns. Also, the focus of the thread is optimizing the use of these regulators, with an emphasis on flat impedance and phase. This premise pretty much disqualifies some of my comments right off the bat. I suppose the only thing that still confuses me is that one can have a flat impedance Zout but not a flat phase. I'll have to think about this.
The phase always turns before the impedance change. If you're referring to the plot in post #209, look carefully at the blue curve, it isn't perfectly flat, there is a slight upward slope to it even before it breaks out. Makes complete sense.
No doubt there will be some peaking somewhere above 20kHz. It will probably be late fall/early winter before I have time to repair my network analyser and measure it. I have an HP 4192A impedance meter in stock now that measures Z/phase up to 13 MHz but it's for resale and I'm not going to risk putting DC on the inputs, but it's tempting!
Stick with the Nat Semi LM337
As can happen when you're connecting/removing parts frequently, I damaged the LM337 in the fixture last night. Grabbed a new 337 (from TI), put it in, and measured to confirm all is well. It wasn't. It looked very much like the LM317 did; Z dip around 500Hz, big Z rise in the 2-5kHz range. Very poor. Not suitable for audio.
Removed it. Put in a new one from Motorola (On Semi). It looked the same. Dug deeper and found another Nat Semi 337, a pull with a 2000 date code. Put it in. Ahhh... that's more like it.
Stick with the Nat Semi 337 to get the results described here.
As can happen when you're connecting/removing parts frequently, I damaged the LM337 in the fixture last night. Grabbed a new 337 (from TI), put it in, and measured to confirm all is well. It wasn't. It looked very much like the LM317 did; Z dip around 500Hz, big Z rise in the 2-5kHz range. Very poor. Not suitable for audio.
Removed it. Put in a new one from Motorola (On Semi). It looked the same. Dug deeper and found another Nat Semi 337, a pull with a 2000 date code. Put it in. Ahhh... that's more like it.
Stick with the Nat Semi 337 to get the results described here.
Just treat the whole chains individually as perfect two-poles, joining to "system GND" right at the load.jbau said:
There is a pitfall with split secondaries with individual bridges: It chops up the leakage capacitances of the xformer which can be pretty high especially with toroids. One should add a capacitive connection from the rectified side to the secondaries that is like 10x greater than the diode's capacitance it has to shunt. Simplest way would be four secondaries, forming two center-tapped chains (or two center-tapped trannies). The center tap only goes to series connected smoothing caps or additional smaller ones paralleled, like it is often seen in tube amp power supplies. And any series L or R in filters should preferably be split up symmetrically.
- Klaus
A different approach
1. I think it's been obvious to many of you that, while flattening the Zout/phase, I've essentially "detuned" the regulator, sacrificing line regulation and output noise in the process. This is the direct result of using larger impedances (smaller capacitor values) in the adjust-to-ground leg. Since I'm no longer focused on the LM317, and since neither the LT1085 or LM337 exhibit instability with larger adjust caps, I decided to seek an alternate route to flatten the Zout while keeping it as low as possible and letting the regs perform at their best.
2. Above approx. 5Khz, the Z flatness is basically determined by the regulator Z divided by the impedance of the output caps. Values in the 1000uF to 1500uF range have given the best results so far. It appears the caps' ESR sets the "floor" of this division.
3. These regs deliver AC current into these low impedance and capacitive loads with significant phase shift.
So I decided to experiment with different output resistors to "buffer" the output from the load, placing them between the LT1085 output and the filter caps/load resistor. The setup:
out to adjust : 100 ohms
adjust to gnd : 1.12k ohms || 10uF tantalum
output cap/load: 1000uF lytic w/ 10uF film || 330 Ohms
This is the same as the last measurement, except the adjust cap is a 10uF tantalum.
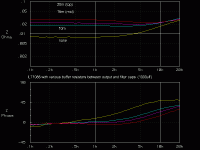
See the graph for Zout and Zphase plots. Buffer resistor values are:
Yellow = 0 Ohm
Cyan = 0.01 Ohm
Violet = 0.015 Ohm
Red = 0.020 Ohm
If you compare these curves to the ones of similar mean Z value generated previously using the detuning approach, you can see they are pretty much the same, except they are smoother. This is evidence of the better line regulation/ripple rejection and lower noise, especially below 500Hz.
The other value of this approach is that it is much more universally applicable. It can be used with ANY regulator to linearize the Z/phase.
The resistors used are "current sense" resistors, commonly used in switching power supplies. One could also use small-gauge wire, but the series inductance would be higher. For example, 26 gauge magnet wire has resistance of 0.041 Ohms per foot. So 6 inches gives you 0.020 Ohms. I cut a piece and verified this. But a single loop of 26 ga. 6 inches long has about 13uH of inductance and significant Zphase. So that's not the best way to go about it.
1. I think it's been obvious to many of you that, while flattening the Zout/phase, I've essentially "detuned" the regulator, sacrificing line regulation and output noise in the process. This is the direct result of using larger impedances (smaller capacitor values) in the adjust-to-ground leg. Since I'm no longer focused on the LM317, and since neither the LT1085 or LM337 exhibit instability with larger adjust caps, I decided to seek an alternate route to flatten the Zout while keeping it as low as possible and letting the regs perform at their best.
2. Above approx. 5Khz, the Z flatness is basically determined by the regulator Z divided by the impedance of the output caps. Values in the 1000uF to 1500uF range have given the best results so far. It appears the caps' ESR sets the "floor" of this division.
3. These regs deliver AC current into these low impedance and capacitive loads with significant phase shift.
So I decided to experiment with different output resistors to "buffer" the output from the load, placing them between the LT1085 output and the filter caps/load resistor. The setup:
out to adjust : 100 ohms
adjust to gnd : 1.12k ohms || 10uF tantalum
output cap/load: 1000uF lytic w/ 10uF film || 330 Ohms
This is the same as the last measurement, except the adjust cap is a 10uF tantalum.
See the graph for Zout and Zphase plots. Buffer resistor values are:
Yellow = 0 Ohm
Cyan = 0.01 Ohm
Violet = 0.015 Ohm
Red = 0.020 Ohm
If you compare these curves to the ones of similar mean Z value generated previously using the detuning approach, you can see they are pretty much the same, except they are smoother. This is evidence of the better line regulation/ripple rejection and lower noise, especially below 500Hz.
The other value of this approach is that it is much more universally applicable. It can be used with ANY regulator to linearize the Z/phase.
The resistors used are "current sense" resistors, commonly used in switching power supplies. One could also use small-gauge wire, but the series inductance would be higher. For example, 26 gauge magnet wire has resistance of 0.041 Ohms per foot. So 6 inches gives you 0.020 Ohms. I cut a piece and verified this. But a single loop of 26 ga. 6 inches long has about 13uH of inductance and significant Zphase. So that's not the best way to go about it.
Attachments
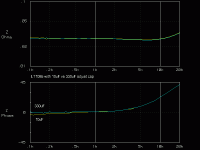
One thing that bothered me about the previous phase curves is that the phase hung below zero from the very start. The only way that happens is if the Z below 100Hz was actually higher and descending downward. This in turn infers that the adjust cap perhaps could be made larger to bring down the output Z below 100Hz and improve the overall flatness. So let's try it with the .020 output R in place.
See the graph below. The yellow curve is with the 10uF adjust cap, the cyan curve is with a 330uF lytic adjust cap. Sure enough, the Zphase below 500Hz is made more linear with the lower impedance on the adjust terminal. We couldn't do this with the LM317 without causing instability and resonance, and because of it's Vin-Vout sensitivity. But the LT1085 doesn't have these issues and definitely benefits from the larger adjust cap in this configuration.
See the graph below. The yellow curve is with the 10uF adjust cap, the cyan curve is with a 330uF lytic adjust cap. Sure enough, the Zphase below 500Hz is made more linear with the lower impedance on the adjust terminal. We couldn't do this with the LM317 without causing instability and resonance, and because of it's Vin-Vout sensitivity. But the LT1085 doesn't have these issues and definitely benefits from the larger adjust cap in this configuration.
Attachments
- Status
- This old topic is closed. If you want to reopen this topic, contact a moderator using the "Report Post" button.