Acoustic Horn Design – The Easy Way (Ath4)

[AllenB]

All these waveguides are top notch (for the size)

You seem to be missing your own point.

The roundover encourages spillover/diffraction outside the wanted dispersion angle. If the device is large enough, that will reduce towards making the idea redundant in the first place.

 

[mabat]

It would be great if you showed me some examples. Otherwise I'm not sure I know what you're talking about (or whether it's correct or not).

 

[AllenB]

I wouldn't know where to start, this has been well discussed on numerous threads.

 

[gedlee]

Maybe so, but I also do not understand your point.

 

[maiky76]

The MMM_ToolboxAxiSym computes DI from complex values of computed pressure(?), which seems to produce incorrect DI curve.

After replacing data.pRad with abs(data.pRad) in the MMM_ASgetDI.m file, the DI for the ST260B is following.

BTW, I had to remove the last 5 points of 250 generated from the coords.txt, because x coordinate was not monotonic.

There is still offset in DI, but the computation seems to follow the (4.144) on the https://www.sciencedirect.com/topics/computer-science/directivity-index

Hi,

The link seems broken can you fix it?

I am rather handy with Matlab/Octave and @Tom Kamphuys already shared his code with me (thanks!).
To me it would be very easy (I think at least) to put the thing into a genetic algorithm for optimization.
This way Matbat indeed keeps complete control over his IP while ABEC/VACS which is costly and not open source, although more precise, is removed from the equation.
I sort of understand that Mabat has already managed to get a GUI based tool for optimization but that's one less thing to worry about with Matlab/Octave.

It would still be possible to use ABEC for verification/fine tuning anyways

I guess now it comes down to
1. Can we fix the MMM_toolbox
2. Can we get the coordinates with the correct format from ATh (that might be what Tom is asking)
3. Get on with it...

 

[fluid]

I am rather handy with Matlab/Octave and @Tom Kamphuys already shared his code with me (thanks!).
To me it would be very easy (I think at least) to put the thing into a genetic algorithm for optimization.

Infinite baffle only in Bjorn's code is quite a significant limitation. Much changes when you add a finite baffle or free space.

 

[mabat]

Listen to him ^.

 

[Kolbrek]

I guess now it comes down to
1. Can we fix the MMM_toolbox

Sorry about this silly mistake! The toolbox has now been updated with pressure magnitude instead of the complex value in the DI calculations.

 

[mabat]

[...]
3. Get on with it...

What might be appreciated by many, I think, is if someone devised a simple direct way of calculating a smooth rollback. Obviously the OS-SE formula itself doesn't allow that as a function y=f(x). We would need to go parametric ([x,y] = [f(t), g(t)]).

I could publish my rollback algorithm but that's just a quick&dirty way of utilizing the discrete profile representation I have inside Ath. I'm not sure it would be universally useful. The basic idea is to smoothly increase curvature along the profile, whatever that may be.

With just the OS-SE and an infinite baffle, you're still only half way there...

 

[mabat]

As a first step we could take an existing profile curve with rollback (e.g. the CE360) and plot its x(t), y(t) components as functions of length along the curve. That could show us what's needed, perhaps something easier to work with than the Fresnel integrals...

 

[Tom Kamphuys]

As a first step we could take an existing profile curve with rollback (e.g. the CE360) and plot its x(t), y(t) components as functions of length along the curve. That could show us what's needed, perhaps something easier to work with than the Fresnel integrals...

I assume the first part is OS. What are f(t) and g(t) (generally, before matching) for the second part?

I'll give it a go. No guarantees though

 

[mabat]

What are f(t) and g(t) (generally, before matching) for the second part?

That's what needs to be found out.

 

[Tom Kamphuys]

I don't have enough information to answer the question directly. So I'll use all degrees of freedom to get the discussion started:

 

[mabat]

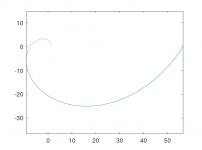
This is what I meant - these are the x(t) and y(t) functions for the CE360 profile, i.e. including the rollback (t=length along the curve).
One would need to construct these two functions as some convenient (analytic) approximations.

- Maybe some sines and cosines would do

 

[Tom Kamphuys]

One could fit a polynomial function of any order or use a spline. But how did you create those lines? (Part of) The answer might be in that.

 

[mabat]

It needs to be parametric in a simple way. This would be without the rollback - these functions look already familiar.

These are the data from coords.txt - a file that's created in the ABEC/Results subdirectory. Point coordinates can be exported from Ath in several ways, that's no problem at all.

 

[mabat]

This is the corresponding target shape, i.e. points [x(t), y(t)].

...And then of course you will need something that can simulate free field radiation (something like ABEC )

 

[Tom Kamphuys]

Still trying to figure out what you want.

The formula for an equi-angular spiral is:

rho(theta) = A*exp(theta*cos(alpha))

x = rho(theta).*cos(theta)
y = rho(theta).*sin(theta)

 

[mabat]

Well I have all I need. I just thought it might be occasionally handy to have a complete profile with rollback in a form of some easy-to-use, parametric analytical description. Of course polar coordinates would work too.

But I guess it won't be so easy.

 

[mabat]

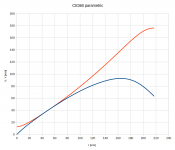
Looking at the picture #9,154, the red curve could be a blend (weighted average) between two hyperbolas and for the blue curve a somehow skewed parabola could do. I might try after all. I just thought that for someone mathematically inclined here this could be a challenge. Remember the equations could bear your name (if they were pretty enough)