You never had any doubt, I'm sure! Although I do expect that at very high frequencies, when the panel wavelengths are no longer so long relative to the panel thickness, there would be more difference. But by then the modes get so close and overlap so much I think it hardly matters, except possibly with respect to coincidence frequency, as we already talked about.Phew!
Eric
And that's when you are not even trying to add edge damping, am I right? That is, trying to make perimeters that are as close to pure hinges or pure clamps as possible, yes? But I think you can easily get far lower Q for the SSSS case if you are trying to do so.I've noticed in my empirical tests that FFFF mode Qs are around 2x what they are in the SSSS or CCCC cases. This effect definitely comes from edge damping
In this example below that I shared earlier, I was using roughly the properties of my carbon/fiber skin balsa core panels for both cases, and where for the SSSS case (in blue) I envisioned Poron foam around the perimeter and used Q=3. I think is realistic based on the measured impedance curves for that panel and mounting. For the FFFF simulation I used Q=25. That may or may not be a little too high for the real free case. But in any case Q is far, far higher than 3 and surely more than 10. I do have actual impedance data for that too and I know it's pretty high Q but didn't really ever try to estimate it with any degree of accuracy.
Eric
Dave,Well, sorta - evanescent waves are part of the solution to the plate differential equation when solved in the time domain (rather than the modal domain), and they are considered non-propagating waves on the surface. Their amplitude under most forcing functions, though, is vanishingly small, and they're almost always ignored in any simulation (like mine). Those waves technically exist at even very low frequencies. The "PIP" effect is more like propagating waves, but a at place where there's a very high density of modes. If you can see multiple wave peaks in the pattern, then it's a propagating wave and not an evanescent wave.
Thanks for clarifying. But I must admit I'm still not sure I understand completely. Bear with me please, and help me if you can and are willing! Below is my own current mental model, where is it right and where is it wrong?
1. We have "transient" waves that form when there is an impulse, or really any change in the signal to the exciter. These travel out from the exciter radially. This is what (I think!) that I mean by PIP. In an infinite plate, these would be the only waves, because there is never any reflection from the perimeter. Likewise, they would be the only waves in a plate with sufficiently low Q, as there would also never be any reflection if waves never reach the perimeter.
2. In a real (i.e., finite) plate, once these waves bounce off the perimeters a few times, they form standing waves, with defined modal shapes, which can be at either low or high frequencies.
2a. In the case of low frequencies, only very few of these modes are "activated" at any given driving frequency, and some of these modes may only have antinodes quite far from the driving point. So at such frequencies we can get standing waves with displacement velocities that can be high anywhere on the panel, since the velocity will be high wherever those modes have antinodes. This is the "modal" frequency region.
2b. In the case of high frequencies, many modes are activated simultaneously. But in this case, since the wavelengths of these modes on the panel are very short, all the activated modes have an antinode very close to the driving point, and all of these modes are (roughly?) in phase with each other in that vicinity. So at the driving point, the average velocity will necessarily be very high. Meanwhile, on the other hand, at any particular point any significant distance from the driving point, some (about half) of the "activated" modes will be moving in-phase with each other, and some other modes (also about half) will be out-of-phase with each other. Hence the net average velocity will tend toward zero, even within a relatively small distance from the driving point. This is the "statistical" frequency region.
All that said:
Is (1) above what you are calling evanescent?
Is (2b) what you are calling propagating waves (even though they are still just a combination of standing waves)?
Other?
Thanks,
Eric
In this example below that I shared earlier, I was using roughly the properties of my carbon/fiber skin balsa core panels for both cases, and where for the SSSS case (in blue) I envisioned Poron foam around the perimeter and used Q=3. I think is realistic based on the measured impedance curves for that panel and mounting. For the FFFF simulation I used Q=25. That may or may not be a little too high for the real free case. But in any case Q is far, far higher than 3 and surely more than 10. I do have actual impedance data for that too and I know it's pretty high Q but didn't really ever try to estimate it with any degree of accuracy.
Eric
I've noticed in my empirical tests that FFFF mode Qs are around 2x what they are in the SSSS or CCCC cases. This effect definitely comes from edge damping, which I plan to eventually add to the model but don't have in there just yet. So for the time being it's probably best to assume something like Q_FFFF = 2*Q_SSSS. But I think this is something that is still open to experimentation!
The low FFFF modes also have lower Qs because they're really high velocity and really low frequency (even relative to the SSSS/CCCC case), so they get damped pretty effectively by the acoustic loading and by the back EMF on the exciter.
Ouch! I am lost. Clarification needed!
From my readings about plate vibration, I was expecting to see some parameters linked to each material to describe its damping property as the elasticity is in the Young modulus E, the mass in the density.
In PETTaLS, the damping property is modeled by a quality factor Q. Why not. I understand it makes fully sense at the level of the response of each modes.
From the exchanges before, I understand now the Q is not only a material property but also dependent of the edge conditions.
When I think a bit deeper to it, it makes sense the Q is linked to the material AND to the edge conditions as it works at the mode level. I was simply not in this way of thinking. I was maybe also encourage in my wrong way of understanding seeing Q listed in the material properties?
Lesson learnt : when I change in the simulator the edge conditions, I have to adapt the Q value also. Correct?
Are there other dependencies of Q ?
@Veleric , @EarthTonesElectronics , Eric, Dave, could you please teach our community about how you get in practice the values of Q?
It may be also a good think that you share how in practice you put a panel in SSSS, FFFF conditions. Those both are theoretical, in practice there is something to hold the panel...
Do you now some readings, papers that would help to understand the relation between the viscous (fluid?) damping that acts as a force proportional to the speed at the plate level, the Q and the edge conditions?
Thank you
Christian
PS: Dave, for the materials proposed, could you tell us for which edge conditions, the Q value is?
I can answer for now, and let Dave tell us the real answer later, haha.From the exchanges before, I understand now the Q is not only a material property but also dependent of the edge conditions.
When I think a bit deeper to it, it makes sense the Q is linked to the material AND to the edge conditions as it works at the mode level. I was simply not in this way of thinking. I was maybe also encourage in my wrong way of understanding seeing Q listed in the material properties?
Lesson learnt : when I change in the simulator the edge conditions, I have to adapt the Q value also. Correct?
Are there other dependencies of Q ?
In Pettals, as it exits today, the Q is intended to be a material property alone, not representing edge conditions. So, in principle, Q is independent of edge conditions.
But that ignores the fact that realistic edge conditions add damping, and hence reduce "Q" of the system. I suggested earlier to Dave that he should add a "reflection coefficient" to the boundary conditions to model this effect. This would represent, say, what fraction of the energy remains when a bending wave reflects at a perimeter, or something similar. I understand that he hopes to do that at some point when he has the time.
The reflection coefficient for "ideal" boundary conditions would be 1.0 for free, simple, or clamped conditions. But I think the practical situation is that only the "free" conditions really approaches that. I suspect clamping a panel edge may also come close 1.0 if the materials are rigid enough, although that is something I have not really tried to confirm. But the usual way to create a "simple" perimeter is with some sort of soft elastic material, like foam, at the perimeter. So of course, whatever that material is will largely determine how much energy is dissipated, and how much remains.
So for the present, since the model does not include a boundary reflection coefficient, my approach is to consider the Q to be a "system Q" which includes both the panel and perimeter damping.
What to choose for Q then is tricky. But my approach is based mainly on the impedance measurement and simulation. By having made enough impedance measurements on many designs, I have a pretty good idea of what the impedance curves of a particular panel and perimeter will probably look like, so I can choose a Q that gives a reasonable impedance curve based on that experience.
I'm pretty sure Q and reflection coefficient are both frequency dependent. But what those look like I don't really have any idea.
Eric
And I'd like to know why changing the Q value has no effect on the output/efficiency of the panel but simply smoothes or accentuates the bumps.
Eucy
Eucy
Oh boy, this is getting pretty complicated. I had to go look up some papers I haven't read in years. Everything you mentioned above would be considered a "propagating" wave. Evanescent waves, specifically, are a very special mathematical case of surface waves that you can expect to never see in a DML setup. I'm pretty sure this is the right way to think about it: if you tie a string to the wall and move it up and down reasonably quickly, you can produce standing wave patterns and/or get a wave to propagate along the string. The Q determines how many wavelengths it's going to take before it decays into nothingness, hence why at high frequencies (short wavelengths) the vibration is concentrated around the exciter (or you, in the case of the string). At low frequencies (long wavelengths), the wavelength is much greater than the panel dimensions so we get reflections and modes before the vibration dies off. If you instead move that string up and down very, very slowly, you'll never get any motion to propagate along the string, no matter how long it is. The string is still moving, though, and we just call this type of motion an "evanescent wave." Everything that's relevant to a DML would be some kind of a propagating wave. If I accidentally called the localized motion an evanescent wave on this forum at some point, that was my mistake. Here is a paper that has some more mathematical information about this type of thing.Dave,
Thanks for clarifying. But I must admit I'm still not sure I understand completely. Bear with me please, and help me if you can and are willing! Below is my own current mental model, where is it right and where is it wrong?
1. We have "transient" waves that form when there is an impulse, or really any change in the signal to the exciter. These travel out from the exciter radially. This is what (I think!) that I mean by PIP. In an infinite plate, these would be the only waves, because there is never any reflection from the perimeter. Likewise, they would be the only waves in a plate with sufficiently low Q, as there would also never be any reflection if waves never reach the perimeter.
2. In a real (i.e., finite) plate, once these waves bounce off the perimeters a few times, they form standing waves, with defined modal shapes, which can be at either low or high frequencies.
2a. In the case of low frequencies, only very few of these modes are "activated" at any given driving frequency, and some of these modes may only have antinodes quite far from the driving point. So at such frequencies we can get standing waves with displacement velocities that can be high anywhere on the panel, since the velocity will be high wherever those modes have antinodes. This is the "modal" frequency region.
2b. In the case of high frequencies, many modes are activated simultaneously. But in this case, since the wavelengths of these modes on the panel are very short, all the activated modes have an antinode very close to the driving point, and all of these modes are (roughly?) in phase with each other in that vicinity. So at the driving point, the average velocity will necessarily be very high. Meanwhile, on the other hand, at any particular point any significant distance from the driving point, some (about half) of the "activated" modes will be moving in-phase with each other, and some other modes (also about half) will be out-of-phase with each other. Hence the net average velocity will tend toward zero, even within a relatively small distance from the driving point. This is the "statistical" frequency region.
All that said:
Is (1) above what you are calling evanescent?
Is (2b) what you are calling propagating waves (even though they are still just a combination of standing waves)?
Other?
Thanks,
Eric
This is the first time I've done much thinking about this topic - my research work had always been using clamped panels, so I only ever looked at relative Q factors using CCCC conditions. Q is actually a parameter for describing resonant peaks (wikipedia), so it's definitely a reductive description for panel parameters. I'm using it to describe the average resonant peak behavior that I observe empirically, but it's also going to be true that all of the mode Qs for any given panel are not going to be exactly the same. In general, the average Q is going to be dependent on both energy loss in the material itself and energy loss in the supports. I've just plugged numbers into pettals that I had observed empirically for CCCC panels, and I guess I hadn't realized how much higher the mode Qs are for FFFF panels. I don't know right now if there are any quick rules that can define this relationship for all materials, but this is something that I'll definitely keep doing research on and updating the simulation tool accordingly!Ouch! I am lost. Clarification needed!
From my readings about plate vibration, I was expecting to see some parameters linked to each material to describe its damping property as the elasticity is in the Young modulus E, the mass in the density.
In PETTaLS, the damping property is modeled by a quality factor Q. Why not. I understand it makes fully sense at the level of the response of each modes.
From the exchanges before, I understand now the Q is not only a material property but also dependent of the edge conditions.
When I think a bit deeper to it, it makes sense the Q is linked to the material AND to the edge conditions as it works at the mode level. I was simply not in this way of thinking. I was maybe also encourage in my wrong way of understanding seeing Q listed in the material properties?
Lesson learnt : when I change in the simulator the edge conditions, I have to adapt the Q value also. Correct?
Are there other dependencies of Q ?
@Veleric , @EarthTonesElectronics , Eric, Dave, could you please teach our community about how you get in practice the values of Q?
It may be also a good think that you share how in practice you put a panel in SSSS, FFFF conditions. Those both are theoretical, in practice there is something to hold the panel...
Do you now some readings, papers that would help to understand the relation between the viscous (fluid?) damping that acts as a force proportional to the speed at the plate level, the Q and the edge conditions?
Thank you
Christian
PS: Dave, for the materials proposed, could you tell us for which edge conditions, the Q value is?
The best way to measure Q factors easily is probably using impedance, as Eric has suggested many times.
Well, it certainly never hurts to have some confirmation. I'm glad that the models align closely, even for mid-frequency modes.You never had any doubt, I'm sure!
@Veleric , @EarthTonesElectronics
+ My apologies to readers allergic to math...
From Dave's thesis, here is the path from the plate governing equation to the displacement as a sum of modes with damping (here for the simply supported SSSS case as shown in the thesis) :

(3.28) makes the link between Q and the b of the governing equation. Q being mode related (r is the index of the modes)
Going a little bit further, Qr equation can be simplified (at least in this SSSS case):

The proposal to write b = µRf comes from a paper I found about one year ago to introduce the damping in my FDM simulation. Rf is a (pure?) material property.
Source : Time-domain simulation of damped impacted plates.
With that it seems the quality factor is mode dependent...
Dave : the paper above is in my understanding more frequency oriented than time domain. It could be also a good source for the visco-elastic damping.
The example of Rf from that source :

+ My apologies to readers allergic to math...
From Dave's thesis, here is the path from the plate governing equation to the displacement as a sum of modes with damping (here for the simply supported SSSS case as shown in the thesis) :
(3.28) makes the link between Q and the b of the governing equation. Q being mode related (r is the index of the modes)
Going a little bit further, Qr equation can be simplified (at least in this SSSS case):
The proposal to write b = µRf comes from a paper I found about one year ago to introduce the damping in my FDM simulation. Rf is a (pure?) material property.
Source : Time-domain simulation of damped impacted plates.
With that it seems the quality factor is mode dependent...
Dave : the paper above is in my understanding more frequency oriented than time domain. It could be also a good source for the visco-elastic damping.
The example of Rf from that source :
@spedge @Veleric
Going back to the topic about two exciters next to each other moving differently, I ran some simulations using my yet-to-be-released high-octane pettals version with multiple exciters, and I found a setup where two exciters close to each other, driven in phase, have very different excursions at some key frequencies. For example, at 40ish Hz, the excursion of one is 10x higher than the other - and from the panel velocity shape, you can see why. This is a FFFF aluminum panel, FYI.

Going back to the topic about two exciters next to each other moving differently, I ran some simulations using my yet-to-be-released high-octane pettals version with multiple exciters, and I found a setup where two exciters close to each other, driven in phase, have very different excursions at some key frequencies. For example, at 40ish Hz, the excursion of one is 10x higher than the other - and from the panel velocity shape, you can see why. This is a FFFF aluminum panel, FYI.
Wired in series?Going back to the topic about two exciters next to each other moving differently, I ran some simulations using my yet-to-be-released high-octane pettals version with multiple exciters, and I found a setup where two exciters close to each other, driven in phase, have very different excursions at some key frequencies.
@Veleric @EarthTonesElectronics
Seems my reading of your thesis Dave was too quick... and that you conclude to a constant Q from practical cases...

Seems my reading of your thesis Dave was too quick... and that you conclude to a constant Q from practical cases...
That is interesting, and a good demonstration of how your model can be useful and informative.I found a setup where two exciters close to each other, driven in phase, have very different excursions at some key frequencies.
As both exciters are on the same side of the nodal line (in dark blue) is it correct that the two exciters locations are in-phase with each other? Is the model at 1 watt? Which exciters did you model?
If we accept that such a thing is possible, would that be evidence that using two exciters is a practice to be sure to avoid?
Eric
Dave,Oh boy, this is getting pretty complicated.
I really appreciate your taking the time to respond to this.
I had to look back at our conversation to try and figure out what we both wrote, and I think I may understand some reasons for our mutual confusion.If I accidentally called the localized motion an evanescent wave on this forum at some point, that was my mistake.
When I spoke of "pebble in a pond" (PIP) waves, you may have assumed I was talking about a surface wave, as waves in a pond surely are surface waves. But I did not intend to imply surface waves at all. What I meant to describe was pure flexural waves (both faces of the panel parallel at any radial position), where the displacement amplitude is greatest at the drive point and the crest of the wave propagates (travels) radially with decaying amplitude as a function of distance.
So when you wrote this (above) I assumed you were referring to my "PIP" waves as "traveling/evanescent" waves. But now I'm pretty sure that's not what you meant. I had focused on the "traveling" part, and ignored the "surface" part, because it never occurred to me that you thought I was talking about surface waves in the first place.Well, because my simulation is a modal one, this is in fact exactly what's happening. I don't ever simulate traveling/evanescent waves on the surface
Eric
Yeah.Wired in series?
I think they were both at 10W, but that was just to get higher excursions. Same polarity. They were EX32HRDS-4 exciters. I think this is similar to a "trampoline" effect, like where pressing down on a trampoline at just the right time can send another person somewhere else on the trampoline flying way up high. It's happening right around the internal resonance of the exciters, which is coupling in a complicated way to the resonances of the panel.That is interesting, and a good demonstration of how your model can be useful and informative.
As both exciters are on the same side of the nodal line (in dark blue) is it correct that the two exciters locations are in-phase with each other? Is the model at 1 watt? Which exciters did you model?
If we accept that such a thing is possible, would that be evidence that using two exciters is a practice to be sure to avoid?
Eric
I wouldn't avoid using 2 (or more) exciters, especially if you want to do some sort of modal tuning setup, but it's best to be aware that you might need to filter out or notch certain frequencies where the excursion is really high.
Oops, I meant to write "NON-traveling/evanescent." Sorry! (also, non-propagating is a better term than non-traveling). I am still always talking about flexural waves, but I was just referring to the modal or PIP pattern we see as "surface waves" (even though I'm well aware that, technically, surface waves are a different type of phenomenon altogether). But anyway, yes, flexural waves can be both propagating waves (modes at low frequencies, PIP pattern at high frequencies) and non-propagating/evanescent waves (which aren't really relevant to the DML discussion). I've noticed that it's pretty difficult to find information on the internet about evanescent waves, and what's there is mostly relevant to optics, so it's a pretty arcane topic. I hope I'm not making this even more confusing!So when you wrote this (above) I assumed you were referring to my "PIP" waves as "traveling/evanescent" waves. But now I'm pretty sure that's not what you meant. I had focused on the "traveling" part, and ignored the "surface" part, because it never occurred to me that you thought I was talking about surface waves in the first place.
@EarthTonesElectronicsAnd I'd like to know why changing the Q value has no effect on the output/efficiency of the panel but simply smoothes or accentuates the bumps.
Eucy
It is low-Q (e.g. internal damping is very high), which makes it sound good with vocals, but it's going to sound "dead" with most music.
So help me out here please:
What does 'dead' look like in a FR graph?
Running through the sims, a perfect FR graph coincides with a Q of 1 (must be an integer and >0), but we all know what that would sound like.
As I asked above, reducing Q just smashes the peaks and does not affect the output - doesn't (intuitively again) sit well with our experiences.
The above graph is Q2 vs 8 on axis - CCCC case 700x300x3 - ply- E 6.6e9, density 450 (poplar)
I know this was asked and answered before but which axis?? as flipping between vertical and horizontal yields the same on-axis FR, so I figure the sim must auto select the major axis ?
Looking at SV around 2.4kHz, with differing Q values, it can be seen that the results just become more fuzzy with decreasing Q, as would be expected with increased damping :
Figures from left to right - Q2, Q5, Q8
I'm finding it difficult to match those figures with the severe dip in the FR graph at this frequency.
And how relevant is an on-axis response graph to output from a multi 'source' DML panel?
What would the FR graph look like if we could sum it @ 0 degrees but over a panel (or part panel) width?
Also of interest to me is that the HF impulse response with Q1 is higher than that with Q5 and Q8 - the LF/MF responses do seem to accord with expectations however:
Left to right Q1,5,8
Perplexed I am
Eucy
Last edited:
Lots of theoretical things that others can jump in on too, but, more importantly, you point out some things that I need to work on fixing...
EDIT: I didn't realize you were just talking about the on-axis FR. This should be the same regardless of the panel orientation. The off-axis horizon-level FRs will change, however, with orientation. So we're all good!
This shouldn't be happening. I need to figure out what's going on here. Thanks for bringing this up.I know this was asked and answered before but which axis?? as flipping between vertical and horizontal yields the same on-axis FR, so I figure the sim must auto select the major axis ?
EDIT: I didn't realize you were just talking about the on-axis FR. This should be the same regardless of the panel orientation. The off-axis horizon-level FRs will change, however, with orientation. So we're all good!
The HF stuff is an artifact that results from the conversion between a logarithmically spaced FR and a linearly spaced FR. I'm going to work on fixing this today.Also of interest to me is that the HF impulse response with Q1 is higher than that with Q5 and Q8 - the LF/MF responses do seem to accord with expectations however:
Last edited:
Hi Dave, thanks for the reply to parts of my queries.
Can you please clarify what your on-axis FR represents. I assumed as it is a theoretically resolved graph that it is an on-axis 'slice' rather than what would be picked up by a physical on-axis omni mic, but if orientation doesn't matter then that can't be the case.
Eucy
Can you please clarify what your on-axis FR represents. I assumed as it is a theoretically resolved graph that it is an on-axis 'slice' rather than what would be picked up by a physical on-axis omni mic, but if orientation doesn't matter then that can't be the case.
Eucy
@EarthTonesElectronicsEric, Dave, could you please teach our community about how you get in practice the values of Q?
Christian,
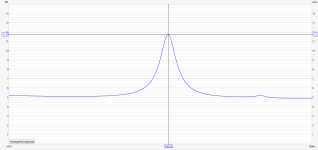
As you know, I have been a proponent of using Impedance testing (among other things) as a measure of relative damping. But until now (that is, now that there is a model that can make use of Q), I have never had a real reason to bother calculating Q values from my measurements.
And I realized (just today) that I'm not really sure the right way to do it!
I know that it should be calculated as f/(f1-f2), where f is the peak frequency and (f1-f2) is the bandwidth. And that if the y axis is SPL, then the bandwith is determined by the -3 dB points. But what if the measured parameter is impedance? Is it at 50% of peak, or 70.7% of peak? And is it at 50% (or 70.7%) of the actual peak value, or at that percentage of the difference between the peak impedance and the baseline impedance?
Below is an an impedance peak from a free panel test I did. Baseline impedance is about 5 ohms, and it peaks at close to 12 ohms.
So do I take the bandwidth at:
a) 5.0+0.5*(12-5)=8.5 ohms
b) 5.0+0.707*(12-5)=9.9 ohms
c) 0.5*12 = 6 ohms
d) 0.707*12 = 8.5 ohms
e) other?
I'm guessing a or b, but what is really correct?
Eric
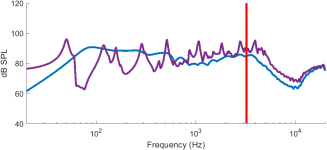
Eucy,As I asked above, reducing Q just smashes the peaks and does not affect the output - doesn't (intuitively again) sit well with our experiences.
In the study I shared here:
Last week I shared details of various methods of evaluating and comparing the damping level in panel speakers. Here I'll share how the frequency response of the various constructions compared.
As you may recall, I tested the same panel in five different mounting configurations.
The panel is a three layer composite with a balsa core and carbon fiber skins, about 2.1 mm thick and with dimensions of 16" x 23.5". In all tests the panel was oriented with the long direction horizontal. The different mountings are described below. Note, I added a new one (#5) similar to 3,4 and 6 with...
As you may recall, I tested the same panel in five different mounting configurations.
The panel is a three layer composite with a balsa core and carbon fiber skins, about 2.1 mm thick and with dimensions of 16" x 23.5". In all tests the panel was oriented with the long direction horizontal. The different mountings are described below. Note, I added a new one (#5) similar to 3,4 and 6 with...
I didn't see much effect of damping on output until I got to very high damping. As soon as I'm sure how to correctly calculate it, I'll try to get Q values for each of those tests.
Eric
Dave,Too many comments to respond to directly - I just uploaded some new versions of the software (again) - you should be able to re-download and re-install easily if you've done so before...
I just loaded the new version today. The surface velocity map works as it should during the simulation run. But after the run is over, if I enter a frequency in the "Frequency" field, nothing happens.
I sometimes had this happen with the original version. It was cleared up in the second version. But in the latest version I have not been able to get a single surface velocity map, except while the simulation is running.
Anyone else having this issue? I fear it's just me.
Eric
- Home
- Loudspeakers
- Full Range
- A Study of DMLs as a Full Range Speaker