Thanks @Veleric! Very interesting and seems to correlate quite well with the FR where 1, 3 and 9 coincides with the prominent peaks.
Small correction to the material data....the GPS I use is 25kg/m³.
I'm trying to figure out the optimum positions to place the padding, and not sure if this data can help me in any way?
I guess I would need more simulations with different positions to get an idea if FR will improve when moving the pads closer to the edges, or placing them on the center of each edge. I did some tests listening to different clamping positions, but need to be more thorough and do some more tests and record the FR.
Small correction to the material data....the GPS I use is 25kg/m³.
I'm trying to figure out the optimum positions to place the padding, and not sure if this data can help me in any way?
I guess I would need more simulations with different positions to get an idea if FR will improve when moving the pads closer to the edges, or placing them on the center of each edge. I did some tests listening to different clamping positions, but need to be more thorough and do some more tests and record the FR.
Please help me out here Eric
I can't see how this free vibration model can relate to a panel which has specific driving points. Eg: can your modes 2,4,5,15 ever exist where the displacement of the driving region is zero.
Eucy
I can't see how this free vibration model can relate to a panel which has specific driving points. Eg: can your modes 2,4,5,15 ever exist where the displacement of the driving region is zero.
Eucy
Eucy,
Indeed, modes like the ones you noted, which show little deflection in the driving region (the center in this case) would not be effectively driven. To drive those modes would require placing exciters elsewhere.
Eric
Indeed, modes like the ones you noted, which show little deflection in the driving region (the center in this case) would not be effectively driven. To drive those modes would require placing exciters elsewhere.
Eric
Eric .. Thanks... And wouldn't it also mean that any mode shown above with blue through the driven point/s would be not achievable.? In fact, one could surmise that it would only be in a low frequency resonance situation in which the maximum panel deflection may conceivably occur away from the driven point/s, and with the semi centrally located multi driver array used by Leob, this is unlikely to occur.
Research by Anderson and co indicates that above the modal crossover frequency of a particular panel, the distributed mode effect is replaced by displacements which are heavily concentrated around each driver. The close spacing of Leob's drivers are likely to result in a spreading of the driving "point", and perhaps unusual stresses on the individual voice coils, perhaps going someway to explaining the damage he's reporting. It is also worth pondering the likely effect of this close cluster on the high frequency performance of the panel.
Eucy
Research by Anderson and co indicates that above the modal crossover frequency of a particular panel, the distributed mode effect is replaced by displacements which are heavily concentrated around each driver. The close spacing of Leob's drivers are likely to result in a spreading of the driving "point", and perhaps unusual stresses on the individual voice coils, perhaps going someway to explaining the damage he's reporting. It is also worth pondering the likely effect of this close cluster on the high frequency performance of the panel.
Eucy
That is a very interesting point.The close spacing of Leob's drivers are likely to result in a spreading of the driving "point", and perhaps unusual stresses on the individual voice coils, perhaps going someway to explaining the damage he's reporting.
Could this mean that the voice-coils experience a lower mechanical impedance than what they're designed for, and thus bottom out too easily?
This might imply that drivers should be spaced out over the relevant nodes instead of being clustered into tight groups, contrary to Dayton et al recommendation.
Not sure, but possible.
I was thinking more in terms of asymmetrical loading due to the panel deflection being greater on the inside of the group than on the outside. Maybe a marginal effect but could cause issues over time
The problem in chasing the nodes is that the mere act of choosing a driver location changes the node patterns available, add another driver and the patterns change again, and so on
I was thinking more in terms of asymmetrical loading due to the panel deflection being greater on the inside of the group than on the outside. Maybe a marginal effect but could cause issues over time
The problem in chasing the nodes is that the mere act of choosing a driver location changes the node patterns available, add another driver and the patterns change again, and so on
I've over-laid Chalmer's nodal line map onto Dayton's recommended driver positioning maps (based on the 2/5ths 3/5ths rules).
It seems there's some disagreement...
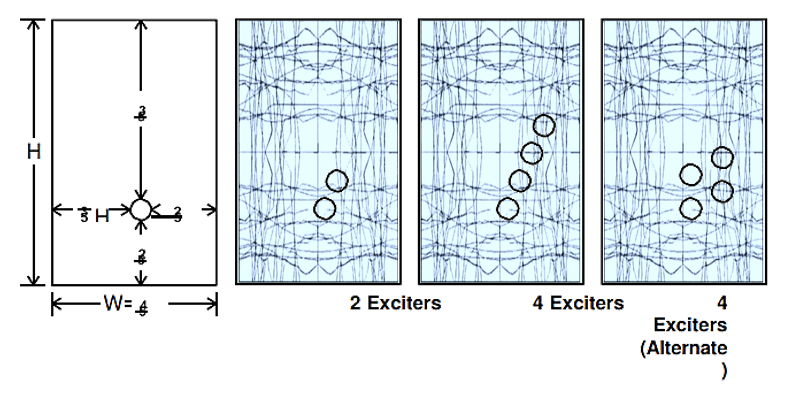
Given the Chalmer's paper, it would seem that the best driver positions should be here:
Or do I misunderstand the thesis?
It seems there's some disagreement...
Given the Chalmer's paper, it would seem that the best driver positions should be here:
Or do I misunderstand the thesis?
You understand the concept, but near the centre is claimed to be the best location, and importantly, it assumes only a single drive point.
So unless the location of each driver in an array is complementary in terms of modal patterns at each frequency (which may in practice be impossible), based on this natural frequency analysis, they will fight against one another, as claimed often by Spedge
In that case, a close cluster would logically perform with less interference than that of a spread pattern, or line array, but still with some disadvantage over that of a single driver, apart from the increased in output volume.
However, can a natural frequency analysis approach be adopted when multiple drivers are used?. I am unconvinced. It seems to me that a full analysis would require superposition of the effects of a number of single driver analyses to optimise the interactions..A massive task... Bring on AI...
Eucy
So unless the location of each driver in an array is complementary in terms of modal patterns at each frequency (which may in practice be impossible), based on this natural frequency analysis, they will fight against one another, as claimed often by Spedge
In that case, a close cluster would logically perform with less interference than that of a spread pattern, or line array, but still with some disadvantage over that of a single driver, apart from the increased in output volume.
However, can a natural frequency analysis approach be adopted when multiple drivers are used?. I am unconvinced. It seems to me that a full analysis would require superposition of the effects of a number of single driver analyses to optimise the interactions..A massive task... Bring on AI...
Eucy
"near"... Operative word. As one can see from the overlay, and from Eric's FEA, dead center driver position drives only the centre nodes horizontally and vertically in straight lines.near the centre is claimed to be the best location
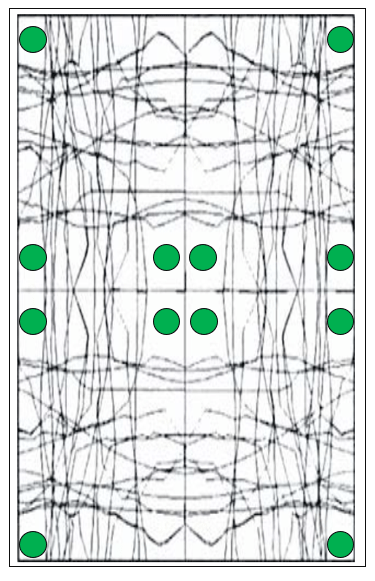
When looking at the chalmers diagrams, for suspension of the the plate, what do you think would give the best results? My thought is that you want to place them on a prominent line to dampen the strongest modes to even out the response. That would mean that if placing them like I have done in the last versions, with two points on each long side, you have to make sure to place them very exactly on the right spot depending on the plate characteristics. But I would assume that the configuration i used before, where I had one point in the middle of each side, should always hit a prominent mode.
This raises the question of which mode to target, and what happens with the energy when you restrict a mode. The FR I posted is a good example since it is has quite prominent peaks from from the first modes:

If damping would simply reduce the response at the frequency of the mode, damping 1 would not do me much good. I don't care much about the response below 100Hz, but even if I did it is already low. Damping 2 would basically make FR drop off earlier then it already does. 3 could do with a bit of reduction, but not really sure what is going on there with the corresponding dip above. Distortion also goes up in that region, and it is like it is fighting itself somehow. I also notice when looking at Erics FEA simulation that the plate is bending very sharply at the suspension points in modes 14 and 15 which is around 800Hz:

That does look stressful.
Is that because it is slightly off a mode, and otherwise it would be able to dampen the mode with less stress, and at the same time make it easier for other less prominent modes to drive the plate more?
@Veleric I would be very curious to see the same simulation but suspended on the middle of each side to see how it compares. If you have to possibility I would be super grateful!
This raises the question of which mode to target, and what happens with the energy when you restrict a mode. The FR I posted is a good example since it is has quite prominent peaks from from the first modes:
If damping would simply reduce the response at the frequency of the mode, damping 1 would not do me much good. I don't care much about the response below 100Hz, but even if I did it is already low. Damping 2 would basically make FR drop off earlier then it already does. 3 could do with a bit of reduction, but not really sure what is going on there with the corresponding dip above. Distortion also goes up in that region, and it is like it is fighting itself somehow. I also notice when looking at Erics FEA simulation that the plate is bending very sharply at the suspension points in modes 14 and 15 which is around 800Hz:
That does look stressful.
Is that because it is slightly off a mode, and otherwise it would be able to dampen the mode with less stress, and at the same time make it easier for other less prominent modes to drive the plate more?
@Veleric I would be very curious to see the same simulation but suspended on the middle of each side to see how it compares. If you have to possibility I would be super grateful!
I also notice when looking at Erics FEA simulation that the plate is bending very sharply at the suspension points in modes 14 and 15 which is around 800Hz:

That does look stressful.
Is that because it is slightly off a mode, and otherwise it would be able to dampen the mode with less stress, and at the same time make it easier for other less prominent modes to drive the plate more?
Leob
Again, I can't see how you would ever generate these modes given the placement of your drivers
Eucy
To me driver placement does not seem essential to what modes can be excited. The plate has its mode structure, and depending on where you place the exciters they will work more or less for or against the existing modes, and the effect is far from absolute. What surprised me was that moving around the clamping seemed to have more effect than moving around the exciter. I think that typically the plate suspension will be a lot more rigid compared to the exciter which is really only adding mass making the mode a little bit harder to excite.
And I don't think the exciter has to be at the peak of a node to excite it to the maximum excursion. It is similar to how a driver interacts with the air mass in a sub, where at some frequencies small movement still results in a lot of air movement at the port or mouth. The exciter ends up in a position where it basically gets leverage against the modes inherent in the plate.
And I don't think the exciter has to be at the peak of a node to excite it to the maximum excursion. It is similar to how a driver interacts with the air mass in a sub, where at some frequencies small movement still results in a lot of air movement at the port or mouth. The exciter ends up in a position where it basically gets leverage against the modes inherent in the plate.
Ok... Take mode 15, (814 hz). How can you generate this pattern when the displacement at the driven point/s is zero? There's no other source of vibration on the plate but your drivers, and in this mode they're not moving.
Mode 14, (800 hz), Your driver grouping would prevent the central displacement pattern from developing, and this will affect the whole plate and the mode pattern
Suggest you try a chladni test at 800 hz to see
Eucy
Mode 14, (800 hz), Your driver grouping would prevent the central displacement pattern from developing, and this will affect the whole plate and the mode pattern
Suggest you try a chladni test at 800 hz to see
Eucy
Blue is not zero, but from zero to 1.053. So up to 1/9 of maximum magnitude. So roughly guessing ignoring other factors, the exciter would have to have a leverage of 1:9 to make the plate edges reach their magnitude.
The plate does not want to bend with any other pattern than its inherent pattern regardless of where you push on it. Try it yourself. Take something thin but stiff that you can hold up between spread out fingers in you hand. A playing card, thin sheet of hard plastic or similar. If you push in the middle it bends down to the middle. If you instead push close to a finger holding up the plate, it is harder to push, and you don't have to push as far, but the bend becomes the same U shape with maximum magnitude of the bend in the middle. The properties of the plate and where you suspend it decides where it will bend, not where you "excite" it to initiate bending.
The plate does not want to bend with any other pattern than its inherent pattern regardless of where you push on it. Try it yourself. Take something thin but stiff that you can hold up between spread out fingers in you hand. A playing card, thin sheet of hard plastic or similar. If you push in the middle it bends down to the middle. If you instead push close to a finger holding up the plate, it is harder to push, and you don't have to push as far, but the bend becomes the same U shape with maximum magnitude of the bend in the middle. The properties of the plate and where you suspend it decides where it will bend, not where you "excite" it to initiate bending.
Last edited:
Hi Leob
I don't believe conflating static deflections with vibration modes is valid.
I'll try to explain my view once more, then we can agree to disagree on this matter.
Take the 814 Hz case again.
On your premise, if an unknown excitation source is producing the pattern, the edges are flapping and the central zone is almost quiescent.
The bending pattern shown has been discretised, with the boundary between zone deep blue and light blue being the 1.053 mm. The central section of the deep blue is indeed zero.
So let's get this frequency activated with the unknown source, then separately energize your unattached drivers at the same frequency. The displacement of the unloaded voice coils will be dependent on the current applied, so let's turn them down to start with, or to simplify it, just assume a single exciter. Now apply the exciter to the central (zero) area of the deep blue zone in a manner that the mass of the exciter is supported. The result... Nothing changes.
Now let's turn up the volume without removing the unknown vibration source.
Suddenly you're imposing a force and displacement to the previous zero zone. This (imo) will certainly disrupt the pattern entirely. Turn off the unknown source and a whole new pattern will emerge.
In summary, I believe that consideration of forced vibration modes cannot be made without reference to the driving point/s. This is especially true with increasing frequencies, where the displacements become more concentrated around the driving point/s. (Ref Anderson and co)
Cheers
Eucy
I don't believe conflating static deflections with vibration modes is valid.
I'll try to explain my view once more, then we can agree to disagree on this matter.
Take the 814 Hz case again.
On your premise, if an unknown excitation source is producing the pattern, the edges are flapping and the central zone is almost quiescent.
The bending pattern shown has been discretised, with the boundary between zone deep blue and light blue being the 1.053 mm. The central section of the deep blue is indeed zero.
So let's get this frequency activated with the unknown source, then separately energize your unattached drivers at the same frequency. The displacement of the unloaded voice coils will be dependent on the current applied, so let's turn them down to start with, or to simplify it, just assume a single exciter. Now apply the exciter to the central (zero) area of the deep blue zone in a manner that the mass of the exciter is supported. The result... Nothing changes.
Now let's turn up the volume without removing the unknown vibration source.
Suddenly you're imposing a force and displacement to the previous zero zone. This (imo) will certainly disrupt the pattern entirely. Turn off the unknown source and a whole new pattern will emerge.
In summary, I believe that consideration of forced vibration modes cannot be made without reference to the driving point/s. This is especially true with increasing frequencies, where the displacements become more concentrated around the driving point/s. (Ref Anderson and co)
Cheers
Eucy
Last edited:
Hi there folks 🙂
( my HYBRID project is slowly coming along. I can hardly wait to post meaningful results )
I tend to think that the combination of 'added mass damping' & selection of suspension points (+ tension)
is probably more effective in controlling 'resonant modes' than the basic location of 1 or 2 exciters somewhere near center.
It does make sense that exciters placed at greater distances apart could 'fight each other', thereby creating unwanted stresses.
Using individual exciters strategically placed to 'forcefully control' modes would surly be complex and require variable drive levels.
At this point, I still intend to use 2 exciters closely located with a small offset from center. Also just two upper & two lower suspension points.
Keep up the good thread - thanks
( my HYBRID project is slowly coming along. I can hardly wait to post meaningful results )
I tend to think that the combination of 'added mass damping' & selection of suspension points (+ tension)
is probably more effective in controlling 'resonant modes' than the basic location of 1 or 2 exciters somewhere near center.
It does make sense that exciters placed at greater distances apart could 'fight each other', thereby creating unwanted stresses.
Using individual exciters strategically placed to 'forcefully control' modes would surly be complex and require variable drive levels.
At this point, I still intend to use 2 exciters closely located with a small offset from center. Also just two upper & two lower suspension points.
Keep up the good thread - thanks
Exactly what was done in another paper by Anderson to force modes using 8 exciters with variable drive levels for each mode.Using individual exciters strategically placed to 'forcefully control' modes would surly be complex and require variable drive levels
Ok for research but obviously not feasible for music.
@Eucyblues99 Not claiming I understand how it works, and is not disagreeing that what you say seems to make some sense. It is just that that is not at all what I observed. If it was correct, then I would think you would hear dramatic shifts in FR when moving the exciter around on the plate. I don't.
Eucy, Leob,
I've been busy the past few days so I've fallen behind a bit. You guys have had too many exchanges for me to reply to them all. That said, I think it's fair to say that I agree with most of what Eucy has been saying about modal behavior.
In a nutshell,
(1) the panel properties, dimensions, and external constraints (i.e supports) determine the full set of modal shapes and their corresponding resonance frequencies.
(2) Driver position effects how effectively each of those modes will be driven.
(3) When the driver is placed exactly along a nodal line (center of the blue areas) the corresponding mode will not be driven at all. When the driver is placed at an antinode (center of the red areas) it will be most effectively driven. At any other place the mode will be driven in proportion to the modes displacement value at the driver position.
A couple of other points:
True, the addition of the driver has some effect on the mode shapes and natural frequencies. So the model of the plate and its suspension (without drivers) only approximates the modes shapes/frequencies of a plate with exciter(s) mounted. The evidence I have, however, suggests that the effect of the drivers (s) is very small for typical plates and exciters. I have shared some of that evidence previously, but will share it again in a separate post.
Also, just because a particular mode is not effectively driven, does not mean that the panel won't radiate sound at that mode's resonance/natural frequency. This point is illustrated in this figure by Hambric.
https://www.hambricacoustics.com/StructuralAcousticsTutorialPart2AcousticsTodayrev1.pdf

If I'm interpreting it properly, the figure suggests that for a driven plate, the sound radiated by a particular mode is effectively zero below that mode's resonance, rises to a peak at resonance, and tends toward a non-zero plateau well above resonance. It's particularly interesting to me that that at the far right of the graph (200 Hz), most of the radiated power is still coming from the 1,1 mode! I honestly think this figure has added as much to my understanding of panels as any other single fact or figure. Basically, it looks like at any given frequency, there will be some contribution from every mode with resonance frequency below that frequency and no contribution from any mode with a natural frequency above that frequency. I'd be interested to know if anyone else has a different interpretation.
The caveat to the above is that there would also be no contribution from modes with natural frequencies below the driven frequency, when the driver is placed at a node of that mode.
Finally, another point illustrated by the figure is that some modes radiate sound better than others. In this example, the plate is driven at 0.25/0.25, which is perfectly located to drive the 2,2 mode, and only moderately well positioned to drive the 1,1 mode. Despite that, the 1,1 mode radiates more power everywhere, including at the resonance frequency of the 2,2 mode!
Eric
I've been busy the past few days so I've fallen behind a bit. You guys have had too many exchanges for me to reply to them all. That said, I think it's fair to say that I agree with most of what Eucy has been saying about modal behavior.
In a nutshell,
(1) the panel properties, dimensions, and external constraints (i.e supports) determine the full set of modal shapes and their corresponding resonance frequencies.
(2) Driver position effects how effectively each of those modes will be driven.
(3) When the driver is placed exactly along a nodal line (center of the blue areas) the corresponding mode will not be driven at all. When the driver is placed at an antinode (center of the red areas) it will be most effectively driven. At any other place the mode will be driven in proportion to the modes displacement value at the driver position.
A couple of other points:
True, the addition of the driver has some effect on the mode shapes and natural frequencies. So the model of the plate and its suspension (without drivers) only approximates the modes shapes/frequencies of a plate with exciter(s) mounted. The evidence I have, however, suggests that the effect of the drivers (s) is very small for typical plates and exciters. I have shared some of that evidence previously, but will share it again in a separate post.
Also, just because a particular mode is not effectively driven, does not mean that the panel won't radiate sound at that mode's resonance/natural frequency. This point is illustrated in this figure by Hambric.
https://www.hambricacoustics.com/StructuralAcousticsTutorialPart2AcousticsTodayrev1.pdf
If I'm interpreting it properly, the figure suggests that for a driven plate, the sound radiated by a particular mode is effectively zero below that mode's resonance, rises to a peak at resonance, and tends toward a non-zero plateau well above resonance. It's particularly interesting to me that that at the far right of the graph (200 Hz), most of the radiated power is still coming from the 1,1 mode! I honestly think this figure has added as much to my understanding of panels as any other single fact or figure. Basically, it looks like at any given frequency, there will be some contribution from every mode with resonance frequency below that frequency and no contribution from any mode with a natural frequency above that frequency. I'd be interested to know if anyone else has a different interpretation.
The caveat to the above is that there would also be no contribution from modes with natural frequencies below the driven frequency, when the driver is placed at a node of that mode.
Finally, another point illustrated by the figure is that some modes radiate sound better than others. In this example, the plate is driven at 0.25/0.25, which is perfectly located to drive the 2,2 mode, and only moderately well positioned to drive the 1,1 mode. Despite that, the 1,1 mode radiates more power everywhere, including at the resonance frequency of the 2,2 mode!
Eric
This post and figure illustrates the effect of the driver location on natural frequencies of a plate, from this post:
https://www.diyaudio.com/community/...s-as-a-full-range-speaker.272576/post-7539933

The three sets of curves are impedance measurements on a single panel with exciter(s) at different locations on the panel. The panel is 14 mm XPS, 48" x 18", supported around the perimeter. In my world, that's a pretty light, flimsy, panel, which I expect would be more affected by the addition of an exciter than a heavy stiffer panel. Exciters were the 25VT-4 and/or 25FHE-4. Heavier, stiffer drivers would have more effect, I expect.
There is one assumption (or is it two?) that you must accept to understand the following assertions. It is that the impedance peaks occur at the natural frequencies of the system, and that the height of those peaks correlates to how well driven the corresponding mode is by the driver in that position. I have done enough modeling and experimentation to be very confident of these points, though I accept also that not everyone may be as convinced. If you are skeptical, see this post:
https://www.diyaudio.com/community/...s-as-a-full-range-speaker.272576/post-7526903
In the set of five curves at the bottom of the figure above, the exciter is located along the center of the short dimension (18") and at 0", 4", 6" or 10" from the center of the long (48") dimension. Note in this set of five curves that regardless of which curve you look at, the natural frequencies are at virtually the same position. Admittedly, there is a noticeable shift at the lower frequencies (especially the 1,1), but by the time you reach the 1,5 mode the peaks are at the same frequency.
Note also, that the height of the impedance peaks varies, depending on the exciter location. For example, the dark red curve (where the exciter was at the center) has peaks only at the 1,1 1,3 1,5 .... modes, because the center is an antinode for those modes. Meanwhile the same dark red curve has no peaks at the 1,2 1,4 1,6 ... modes, because the center is a node for those modes, hence they are not driven at all with the exciter in the center.
Meanwhile, the curve with the strongest peak near 60 Hz (the 1,2 mode), is the one with the exciter placed at 10 inches from the center. This is because it is the exciter position closest to the antinode of the 1,2 mode (theoretically at 12 inches).
All in all, my conclusion is that the effect of exciter position is not huge on the natural frequencies (and likely also not on the mode shapes either), particularly for modes above the first 2 or 3. So I think the analysis of the plate without drivers give a very good indication (though not perfect) of the mode shapes and frequencies of the same panel with exciters attached.
Eric
View attachment 1276751
https://www.diyaudio.com/community/...s-as-a-full-range-speaker.272576/post-7539933
The three sets of curves are impedance measurements on a single panel with exciter(s) at different locations on the panel. The panel is 14 mm XPS, 48" x 18", supported around the perimeter. In my world, that's a pretty light, flimsy, panel, which I expect would be more affected by the addition of an exciter than a heavy stiffer panel. Exciters were the 25VT-4 and/or 25FHE-4. Heavier, stiffer drivers would have more effect, I expect.
There is one assumption (or is it two?) that you must accept to understand the following assertions. It is that the impedance peaks occur at the natural frequencies of the system, and that the height of those peaks correlates to how well driven the corresponding mode is by the driver in that position. I have done enough modeling and experimentation to be very confident of these points, though I accept also that not everyone may be as convinced. If you are skeptical, see this post:
https://www.diyaudio.com/community/...s-as-a-full-range-speaker.272576/post-7526903
In the set of five curves at the bottom of the figure above, the exciter is located along the center of the short dimension (18") and at 0", 4", 6" or 10" from the center of the long (48") dimension. Note in this set of five curves that regardless of which curve you look at, the natural frequencies are at virtually the same position. Admittedly, there is a noticeable shift at the lower frequencies (especially the 1,1), but by the time you reach the 1,5 mode the peaks are at the same frequency.
Note also, that the height of the impedance peaks varies, depending on the exciter location. For example, the dark red curve (where the exciter was at the center) has peaks only at the 1,1 1,3 1,5 .... modes, because the center is an antinode for those modes. Meanwhile the same dark red curve has no peaks at the 1,2 1,4 1,6 ... modes, because the center is a node for those modes, hence they are not driven at all with the exciter in the center.
Meanwhile, the curve with the strongest peak near 60 Hz (the 1,2 mode), is the one with the exciter placed at 10 inches from the center. This is because it is the exciter position closest to the antinode of the 1,2 mode (theoretically at 12 inches).
All in all, my conclusion is that the effect of exciter position is not huge on the natural frequencies (and likely also not on the mode shapes either), particularly for modes above the first 2 or 3. So I think the analysis of the plate without drivers give a very good indication (though not perfect) of the mode shapes and frequencies of the same panel with exciters attached.
Eric
View attachment 1276751
- Home
- Loudspeakers
- Full Range
- A Study of DMLs as a Full Range Speaker