@tktran303: I am using the following SB 15inch woofer (for subwoofer duties):
https://www.sbaudience.com/index.php/products/subwoofers/nero-15sw800/
The other 15inch I am using is the Faital pro 15PR400 (goes higher up in frequency to low mids)
https://www.sbaudience.com/index.php/products/subwoofers/nero-15sw800/
The other 15inch I am using is the Faital pro 15PR400 (goes higher up in frequency to low mids)
The edge termination business of the waveguide and connecting it to a rectangular box has been on my mind..
Till now, I have been using circular arcs to join the waveguide to the box that holds it. Inspired by @tmuikku's comments about 'matching' curves, I thought, why not use a super elliptic curve defined over one quadrant as the piece to connect the waveguide to the box instead of a circular arc.
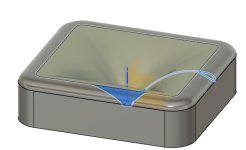
So I took the parameters of the super ellipse (except parameter L) from the ATH profile definition (of this OSSE waveguide) and created a smaller super ellipse of L=44mm to serve as the edge termination.. This is how it looks 😀
The waveguide alone is the yellow surface. The edge termination solid body has been extruded from the smaller (approximation using splines) super ellipse I created..
I haven't simulated the effect of this over the cirrcular arc in ABEC sims though.. I am feeling lazy to check that part.. 😀
Till now, I have been using circular arcs to join the waveguide to the box that holds it. Inspired by @tmuikku's comments about 'matching' curves, I thought, why not use a super elliptic curve defined over one quadrant as the piece to connect the waveguide to the box instead of a circular arc.
So I took the parameters of the super ellipse (except parameter L) from the ATH profile definition (of this OSSE waveguide) and created a smaller super ellipse of L=44mm to serve as the edge termination.. This is how it looks 😀
The waveguide alone is the yellow surface. The edge termination solid body has been extruded from the smaller (approximation using splines) super ellipse I created..
I haven't simulated the effect of this over the cirrcular arc in ABEC sims though.. I am feeling lazy to check that part.. 😀
Thatcway ypu can see if there is a (gross sudden) change in curvature.
In fusion 360, there is an option to view the curvature for splines (Don't know if this is exactly the curvature, which is computed as the derivative of the function but I hope it is)..
Anyway, I toggled it on on a cutaway of the waveguide and here is how it looks.
The red color curve is the curvature
Zoomed in pic
There is a discontinuity showing big curvature jump at the waveguide edge, which is probably due to my spline fit not properly done (so not a thing to worry about) or in the very rare chance, something which is native to this waveguide itself (and will go away with edge termination). After that big discontiuity is an L =2.7mm super elliptical curve (with the same parameters as that of the horn except L ) that I joined to the wavguide edge..
The curvature changes gradually till the sharper turn begins, jumps around and then becomes smooth again..
I dont know what magnitude of jumping around causes the waves reaching that point to difract seriously.. but this is how it looks.. 🙂
Anyway, I toggled it on on a cutaway of the waveguide and here is how it looks.
The red color curve is the curvature
Zoomed in pic
There is a discontinuity showing big curvature jump at the waveguide edge, which is probably due to my spline fit not properly done (so not a thing to worry about) or in the very rare chance, something which is native to this waveguide itself (and will go away with edge termination). After that big discontiuity is an L =2.7mm super elliptical curve (with the same parameters as that of the horn except L ) that I joined to the wavguide edge..
The curvature changes gradually till the sharper turn begins, jumps around and then becomes smooth again..
I dont know what magnitude of jumping around causes the waves reaching that point to difract seriously.. but this is how it looks.. 🙂
Last edited:
I think it is ok. The waveguide gors to almost straight. The wiggle is math, the real shape is most likely not so exact, and sanding an finishing will make it smooth anyhow.
I tried a spline fit of the super ellipse with more points.. The wiggles in curvature seems definitely due to the approximation of the super ellipse using spline in fusion.. Here is the result with more points in the approximation
I just wish I could plot the equation in fusion instead of importing csvs and doing spline fits..
Anyway, I will try to go with this, just so that I don't lose the forest for the trees.. 😀
There are more important things to worry about in the overall design of this MEH waveguide..
I just wish I could plot the equation in fusion instead of importing csvs and doing spline fits..
Anyway, I will try to go with this, just so that I don't lose the forest for the trees.. 😀
There are more important things to worry about in the overall design of this MEH waveguide..
When the waveguide has been designed to transition to a flat baffle like this one, you cannot extend the curvature to create a single curve. Whether it is a radius or a more complicated shape will have relatively little difference unless the effective size changes.
To have a continuous curve the whole thing has to be redesigned so the curvature begins to change much earlier and that can take some trial and error.
Last edited:
Why not? The curvature of the waveguide goes to zero near the edge, so it simply takes another curve that starts at zero curvature, like the superellipse used, basically.
To me it seems Vineeth knows very well what he is doing.
I indeed disagree, as I think it's false, no matter how many times I read it. It just makes sense to keep the curvature smooth in any case.
This is simply not true, but it seems you don't like your claims being questioned.
No what I said and you said are the same to me. I don't see disagreement but you managed to find it and be rude about it, well done.
Your first reaction to my question was ad hominem attack, which is not very polite. But perhaps you just don't understand what continuous means, then I would understand the "confusion".
Thanks @mabat and @fluid for all the suggestions.. I find all of them valuable.. Both of your suggestions/comments helps me think better, sometime take a. step back and rethink about the same thing etc.. All this has only improved my projects.
Now I am sorry for all the confusion above. My idea was exactly what mabat told.. Take a curve (of the waveguide) whose curvature goes to zero at the edge and connect it with another curve that has the same curvature in the region and let it transition smoothly afterwards.. This is why I tried using the super ellipse. Given that I shouldn't be ideally altering the profile of the ATH generated waveguide, this is the best I could think of..
From what fluid mentioned, what I understood is that my approach has a little bit of a fundamental flaw in the sense that I took a waveguide designed for infinite baffle (which sort of fixes the curvature transition towards the edge) and then tried to put it in a box, for which it was not optimized for.. Maybe if I was to do it the right way, I should have taken the box/construct that holds the waveguide and then start the optimization of the waveguide (from scratch) having this constraint in place (that the waveguide is going to be fixed to this particular chosen box).. The resulting overall waveguide wall dimension increase (waveguide + termination curve) might contribute more to the overall polar pattern also..
I think this along the lines of what @lrisbo also mentioned, per my limited understanding.
Anyway, since I lack the tools the to do the full automatic optimization of the waveguide with the final box shape also considered (unless I do it manually using ATH using several trial and error approaches/ iterations), I will continue with the current approach for now..
I need both (all) of you on this thread.. so please let's put behind our confusions and move forward.. 🙂
Now I am sorry for all the confusion above. My idea was exactly what mabat told.. Take a curve (of the waveguide) whose curvature goes to zero at the edge and connect it with another curve that has the same curvature in the region and let it transition smoothly afterwards.. This is why I tried using the super ellipse. Given that I shouldn't be ideally altering the profile of the ATH generated waveguide, this is the best I could think of..
From what fluid mentioned, what I understood is that my approach has a little bit of a fundamental flaw in the sense that I took a waveguide designed for infinite baffle (which sort of fixes the curvature transition towards the edge) and then tried to put it in a box, for which it was not optimized for.. Maybe if I was to do it the right way, I should have taken the box/construct that holds the waveguide and then start the optimization of the waveguide (from scratch) having this constraint in place (that the waveguide is going to be fixed to this particular chosen box).. The resulting overall waveguide wall dimension increase (waveguide + termination curve) might contribute more to the overall polar pattern also..
I think this along the lines of what @lrisbo also mentioned, per my limited understanding.
Anyway, since I lack the tools the to do the full automatic optimization of the waveguide with the final box shape also considered (unless I do it manually using ATH using several trial and error approaches/ iterations), I will continue with the current approach for now..
I need both (all) of you on this thread.. so please let's put behind our confusions and move forward.. 🙂
That's exactly right, that is the best what you can do with the existing (OSSE) waveguide. This way you can create one smooth (or at least continuous-curvature) curve - it's not true that this is not possible. There's probably no single (simple) analytic description of it, but that's irrelevant.
A short path to a solution is a spline with 4 control points. And play with the position of the middle 2 cpoints as long as the vector with endpoint remains inline with waveguide and on other end with enclosure. Either way the physical waveguide enclosure will never be that precise. And i doubt about the impact on sound radiation.