Semi-Le_calc predicts the phase response from the reactive nature of the circuit model that it uses. It's able to estimate the values of the components in that model using only the magnitude response of the impedance data. Having solved the estimation problem, it simply computes the impedance using the reactive impedance values of the inductors and capacitors as a function of frequency. The equivalent circuit model is quite compact, so the impedance can be calculated using just a few computational steps.
Last edited:
The results vary (drastically for Rss), if I change Include Marker 2 from 10k to 20k. When I then set it down to 10k again, they stay similar to the 20k results. Rss stays very high.
Did you use the auto trace option, or did you manually pick all the points on the impedance curve? If you used auto trace, the curve is likely to have a bit of "noise" on it that shouldn't be there (at least that's what I saw happening). That might be making it more difficult for the least squares solver. Using the data between 20Hz and 10,000Hz makes perfect sense.
I used auto trace. I could have a look at the txt file and look for odd numbers; but the graph above looks very clean to me?
But my main questions remain: why do bolserst and I get different results (are they in an acceptable corridor, because we used slightly different input curves), which results are more realistic and how can I achieve a better result for Rss?
But my main questions remain: why do bolserst and I get different results (are they in an acceptable corridor, because we used slightly different input curves), which results are more realistic and how can I achieve a better result for Rss?
If I was trying to lock anyone out I would have used a much stronger word than "unusual." I'm really just trying to understand the range of uses for this parameter and where it usually shows up. I'm not here to police anyone's enjoyment of this hobby.
I got some additional data from LaVoce in the meantime. Now I have L2, R2, Cmes, Lces, Res.
These values are used for another semi-Le model, as far as I understand. But can they be converted to the values Re', Leb, Le, Ke and Rss that we need for hornresp?
These values are used for another semi-Le model, as far as I understand. But can they be converted to the values Re', Leb, Le, Ke and Rss that we need for hornresp?
Unfortunately no, there is no way to analytically determine Semi-Le parameters from the L2, R2 values. The L2, R2 model is an effort to try and capture some of the semi-inductance effect, but it will only provide a good match for the blocked impedance over about 3 octaves. If you can share the values we can plot up the results to compare with the measured impedance.
I think the main reason for the difference in Mms is that you used Vas = 238 ltr instead of the datasheet value of 245.
I would use the Qes and Qms values that the spreadsheet comes up with since the datasheet values likely come from a traditional TSP utility which assumes a symmetric impedance peak and does not account for the skewing of the peak by the semi-inductance. See Post #51.
The reason is that we are using a simplified 5 parameter version of the full 15 parameter Sem-Le model and there is not an analytical solution to determine their values from an impedance curve. Instead we must use a Least-Squares magnitude matching technique. There may be a dozen or more local minimums in the Least-Squares design space. So depending what the starting values are for the 5 parameters, you might wind up with slightly different “acceptable” results. If I am not getting a near perfect match, I usually try several different starting values sets. Also, sometimes an additional run of the LS-fit routine from the existing solution will provide a slightly better fit. Comparing the results I posted with yours you can see a slightly better fit for my values. But, in the end, what you care about is how it affects your enclosure modeling. Usually if you get this close, the enclosure modeling will be just fine.
Also, as witwald mentioned, with the simplified 5 parameter model it is a good compromise to give up some matching above 10kHz if it improves the match below 5khz which will better define the semi-inductance parameters and provide better enclosure modeling.
I don't know what todo with that; the values are completely different from the ones at their website or PDFs. Fs is up to 36Hz from 30Hz; which doesn't correspond with the impedance graph they provide. A already wrote back to the distibutor and asked for an explanation.
Note that Vas is only 158ltr compared to 245ltr on the PDF data. However, the Mms is about the same. Most likely this data was taken with the driver cold or not broken in yet. If you leave all other physical/electrical parameters the same but increase the compliance to 245ltr, Fs would change to 29.24 Hz, and Qes would change to 0.344...in line with the PDF data. See equations below for relationships between TSP and physical/electrical parameters.
Looking at the frequency dependent inductance for the R2L2 data, it matches reasonably well with the Semi-Le model derived from the measured impedance only between 100-1000Hz.
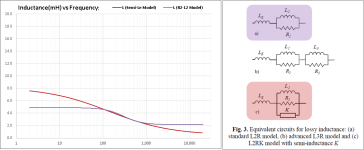
Looking at the frequency dependent inductance for the R2L2 data, it matches reasonably well with the Semi-Le model derived from the measured impedance only between 100-1000Hz.
I got an answer from Italy that confirms your suspicions ;-)
I would never have thought that they would take two new drivers from the current production and measure them for me ;-)
But that also means that these measurements are practically useless because these were not run-in drivers that had been tested under real conditions.
So I would use the data you suggested, or can we get some added value from the measurements from Italy?
Code:
The T/S parameters I provided are very recent and pertain to two new speakers.
I’m not particularly concerned about the slight differences between these measurements and the nominal values specified in the official datasheet.
I understand that some non-professional customers might expect 100% consistency between the declared and measured values, but this is physically unrealistic.
In this specific case, I believe the primary factor influencing the results is the temperature at the time of measurement, which likely caused the compliance to be significantly lower than the nominal value.
Additionally, the moving mass (the total of the cone, surround, spider, voice coil, and glue, with a normal declared tolerance equal to 15%) is about 3.5% less than the nominal value and this contributes to the observed differences.I would never have thought that they would take two new drivers from the current production and measure them for me ;-)
But that also means that these measurements are practically useless because these were not run-in drivers that had been tested under real conditions.
So I would use the data you suggested, or can we get some added value from the measurements from Italy?
By virtue of it being under a square root sign, a 3.5% change in moving mass will result in roughly half that much change in the resonance frequency Fs. That is, it produces only a 1.73% change in Fs, which is quite small in the overall driver parameter scheme of things. It amounts to about a 0.52Hz shift in a driver with a resonance frequency of 30Hz.
I agree entirely.
With this kind of data, which is quite typical if taken from datasheets, the nonlinear least squares estimator has a very difficult time of things. When doing my own curve fitting, I discovered that the estimated value of Re' was actually below that of Rvc (the DC resistance of the voice coil at 0Hz). This seems to be a spurious result that needs to be handled appropriately.
I followed this suggestion and obtained the following results, using Sd = 1225 cm^2 from the data sheet for the Lavoce SAF184.03 provided earlier. The curve fitting seems to have produced an excellent result, with the impedance model matching the measured data very well.
Below is a zoomed-in view of the impedance curve fit around the resonance peak. The curve fit has overestimated the height of the peak.
If we set the value of Re' to be equal to Rvc = 5.8 ohms (the value in the datasheet), we obtain the following improved fit of the impedance peak.
For this curve fit, we have obtained Qms = 7.037, Qes = 0.355, and Qts = 0.338. This compares very favourably with the datasheet values: Qms = 6.7, Qes = 0.34, and Qts = 0.32.
The above results and general behaviour suggest that an improved curve-fitting methodology can be developed. In this instance, there appears to be a good case for splitting the Re' term into two parts: Re' = Rvc + Re". The value of Rvc can easily and accurately be measured using a multimeter. The curve-fitting process can then simply estimate the value of Re".
If such an approach is implemented, it could be expected to improve the quality of the curve-fits. That's because it will prevent Re' from dropping below the value of Rvc, which is what happened when initially curve-fitting the impedance of the Lavoce SAF184.03 woofer.
Last edited:
What datasheet are you using? Where is VAS 245l from? I use the datasheet from here:
https://lavocespeakers.com/single-product/?id=93
Qes 0.35
Qes 6.73
VAS 223.28
I agree; Re' is often lower than Re when using this curve, so you probably have to set Re' manually. Can we estimate from the manufacturer's other data whether 1.1*Re or higher or lower is closer to reality? I got "good" but different results for the rest of the parameters with Re' from 6 to 6.5 ohms...
A few more observations:
- If I move the curve sideways by just one pixel (or move the markers one pixel in the auto trace), the results change significantly. So the results will always be a fuzzy approximation unless we have better data than just the impedance curves read from graphs.
- Once the simulation has determined an Rss, it stays there even if I manually change other values and click on "LS-fit". To reset the fitting routine, I often start with manually adjusted Rss and see how the other values develop and only check the box in front of Rss later.
https://lavocespeakers.com/single-product/?id=93
Qes 0.35
Qes 6.73
VAS 223.28
I agree; Re' is often lower than Re when using this curve, so you probably have to set Re' manually. Can we estimate from the manufacturer's other data whether 1.1*Re or higher or lower is closer to reality? I got "good" but different results for the rest of the parameters with Re' from 6 to 6.5 ohms...
A few more observations:
- If I move the curve sideways by just one pixel (or move the markers one pixel in the auto trace), the results change significantly. So the results will always be a fuzzy approximation unless we have better data than just the impedance curves read from graphs.
- Once the simulation has determined an Rss, it stays there even if I manually change other values and click on "LS-fit". To reset the fitting routine, I often start with manually adjusted Rss and see how the other values develop and only check the box in front of Rss later.
The datasheet that I used was the one that was attached to Post #48: here.
Although the Thiele–Small parameters are different between the two sets of datasheets, the impedance response curves appear to be identical, as do the two SPL frequency response curves. The value of Fs = 30Hz in both datasheets. The other parameters do have some differences, but those differences are relatively minor.
As the impedance curves are essentially the same, the curve-fit differences seem to be indicative of some sort of sensitivity in the impedance model. Although I believe that Re' should never drop below Rvc, whereas it did in one of the curve-fits that I performed.
Interestingly, when Re' is treated as a constant (fixed) parameter, the closer in value to Rvc that it gets, then the better the curve-fit of the impedance peak that is obtained. By better, I mean that the peak impedance value and the values on the left and right slopes either side of the peak are all more closely matched by the estimated parameters when Re' is similar in value to Rvc (Re in the datasheets).
Keep in mind that the impedance data used by the nonlinear least squares curve-fitter consists of many points. My impedance data consists of over 470 points. The model's component values seem to produce an excellent curve fit, so they should give reliable Thiele–Small parameter estimates when they are substituted back into the appropriate equations.
Although the Thiele–Small parameters are different between the two sets of datasheets, the impedance response curves appear to be identical, as do the two SPL frequency response curves. The value of Fs = 30Hz in both datasheets. The other parameters do have some differences, but those differences are relatively minor.
As the impedance curves are essentially the same, the curve-fit differences seem to be indicative of some sort of sensitivity in the impedance model. Although I believe that Re' should never drop below Rvc, whereas it did in one of the curve-fits that I performed.
Interestingly, when Re' is treated as a constant (fixed) parameter, the closer in value to Rvc that it gets, then the better the curve-fit of the impedance peak that is obtained. By better, I mean that the peak impedance value and the values on the left and right slopes either side of the peak are all more closely matched by the estimated parameters when Re' is similar in value to Rvc (Re in the datasheets).
Keep in mind that the impedance data used by the nonlinear least squares curve-fitter consists of many points. My impedance data consists of over 470 points. The model's component values seem to produce an excellent curve fit, so they should give reliable Thiele–Small parameter estimates when they are substituted back into the appropriate equations.
Last edited:
It's now come to my attention that Re' has to be found by curve fitting and not by measuring DC resistance, the latter giving us Re (aka Rvc). However, if the curve-fitter in Semi-Le_calc that we have been using is allowed to try and estimate Re' from the impedance data, it seems to produce a poor estimate. This is evident when the estimated value of Re' < Re.
That's interesting. By "markers" I assume that you mean the lines used to set the range of the impedance, SPL, and frequency values when performing point data extraction. Depending on the resolution of your plot, that single pixel will produce a large shift in the data values, and this will lead to different estimates from the curve fitter. When you say "the results change significantly", do you mean 1–2%, or by more than that?
I've also noticed that type of behavior in the Rss values. I don't know why it occurs. It could be an example of ill-conditioning of some sort.
One thing I tried was to delete the value in the Rss cell entirely, leaving it blank. Clicking "LS-fit" after that seems to produce a more reasonable-looking estimate for Rss, while still maintaining a good curve fit to the impedance data.
When Thorborg and Unruh were curve fitting the impedance of a Peerless woofer, for the driver in question Re = 5.83 ohms, and the curve fitter obtained Re' = 6.24 ohms using their new model. This was 0.41 ohms above Re alone. Since the Lavoce SAF184.03 has a demodulating ring, it would seem that an Re' value of at least 5.8+0.4 = 6.2 ohms would not be unreasonable. If the curve fitter produces something less than that, then we might have a bit of a problem.
Last edited:
Unfortunately, I didn't write down any details last night; I just noticed that the calculated values always differ quite widely, or that many different groups of values lead to similar simulated impedance curves. Especially for Re' and Rss, you would need more information than just the impedance curve, which obviously offers many possibilities for approximation.
Fortunately, these different calculated values usually lead to very similar simulations in the 30-100Hz range, which is what I'm interested in, so it doesn't seem to matter much which approach you take to approach the impedance curve. However, I think you would get results that are closer to the truth™ if you could estimate and specify the values of Re' and Rss within a reasonable range. In the case of the SAF184.03 (with the missing data below 20Hz) the curve fitter almost always gives me Re' values below Re and I have to correct them manually based on my feeling.
Fortunately, these different calculated values usually lead to very similar simulations in the 30-100Hz range, which is what I'm interested in, so it doesn't seem to matter much which approach you take to approach the impedance curve. However, I think you would get results that are closer to the truth™ if you could estimate and specify the values of Re' and Rss within a reasonable range. In the case of the SAF184.03 (with the missing data below 20Hz) the curve fitter almost always gives me Re' values below Re and I have to correct them manually based on my feeling.