I checked my notes from many, many years ago, found an equation, tested it out and found it to be wrong, LOL, and I corrected it:
Ripple = IF(S<0.7071,20*LOG(((1/(2*S))^4/((1/(2*S))^2-0.25))^0.5),0)
Yes, there's a logic test in there, as the equation is not applicable if S is higher than 0.7071.
TBH, I'm not sure much emphasis should be put on the "Ripple" as whatever "Ripple" is going to happen in the sim's passband is going to be visible in the FR graph anyway. The calculation was of more value back when we were using calculators, not computers or simulation programs. Also, it seems to fall apart at high Gain values (based on the FR graphs I'm seeing for a few sims).
Well, after several hours of reviewing calculations and sims, I think I figured it out, and at the same time reminded myself at the same time of one of the two reasons why I stopped using the tables and calculations for BP design work so many years ago, LOL. The answer was actually hiding there in plain sight ...
The LDC tables and the associated calculations do not take into account the driver's inductance, Le!
Zero out the driver's inductance in the Hornresp sim, and the predicted FR of a 4th order BP alignment looks like it might be a LOT closer to what's predicted by the tables (and the calculations). I haven't done direct comparisons yet, but the Hornresp sims are now producing flat passbands for Q=0.7 at different Gain settings, so I think that's a pretty good sign that Le was the cause.
Of course, subwoofer drivers with zero inductance simply don't exist. So maybe a note should be included with that routine in Hornresp to indicate that driver inductance is not being considered and the sim will have to be adjusted accordingly to get the best results. A possible alternative would be to include an optimization routine that shifts Fb upward to compensate for driver inductance. I've got an idea about how to do that if you're interested.
I also found an error in my bandpass frequency response equations concerning how they handle box losses, but that's a whole other story ...
Many thanks!
It was decided to show Ripple magnitudes rather than S values because they are considered to be more meaningful to the average user.
The three existing options (0.00 dB, 0.35 dB and 1.25 dB) will be retained, but no more added.
Thanks for taking the time to look into this. Not including the effect of Le is a limitation of any model based on classical Thiele-Small filter theory.
While we could perhaps be accused of "fudging the formulas", I would certainly be very interested if it has the potential to generate a more optimised overall result.
Maybe instead of "S", show Qbp? That should be a lot easier to understand, and S can be calculated from it, by reversing the equation I shared previously showing the relationship between S and Qbp. The ripple magnitudes are going to be inaccurate anyway because the LDC method and the calculation I provided don't take driver inductance into account.
It's not a fudge, more a "solution via iteration" 🙂 . It basically assumes that the "optimum" solution is a symmetrical response in the passband near to Fb.
After selecting Fb via the existing method, sample the response just above and below Fb (e.g. +/- 1/16 octave), call this Fb1 and Fb2. If the magnitude response is the same, then Fb is at the optimum value. If not, use the magnitude values at Fb1 and Fb2 to estimate a more optimum value for Fb. Repeat if necessary.
Not sure how best to do that, as the primary relationship is between Qbp and sensitivity/gain, not Qbp and S/ripple. The slider could show Qbp values which would vary depending on the selected value of S, but this could be confusing and less meaningful than just continuing to show the gain values.
After thinking about it for a while, unfortunately I can see problems in trying to implement the suggested method, given the inputs being used. It is probably better to just leave things as they are, with the procedure being:
1. For a given driver, work through the different valid combinations of S/ripple and sensitivity/gain to find the setting that gives the response closest to what is required. **
2. Using the above response as a starting point, further manually adjust the Vc1, Vc2, Lc1, Lc2, Ap1 and Lp1 sliders to refine the result as necessary.
** This is consistent with the Vance Dickason recommended approach - "The recommended procedure is to start with Table 1.25, S = 0.7, and by trial and error determine whether or not the driver selected will provide the desired fL and fH frequencies at the sensitivity level required. This can be done for different levels of sensitivity until a satisfactory compromise between fL/fH frequencies and sensitivity is determined."
1. For a given driver, work through the different valid combinations of S/ripple and sensitivity/gain to find the setting that gives the response closest to what is required. **
2. Using the above response as a starting point, further manually adjust the Vc1, Vc2, Lc1, Lc2, Ap1 and Lp1 sliders to refine the result as necessary.
** This is consistent with the Vance Dickason recommended approach - "The recommended procedure is to start with Table 1.25, S = 0.7, and by trial and error determine whether or not the driver selected will provide the desired fL and fH frequencies at the sensitivity level required. This can be done for different levels of sensitivity until a satisfactory compromise between fL/fH frequencies and sensitivity is determined."
I am missing the point of calculating certain volumes and such by (empirical) formulas to begin with?
I'd rather work with target curves.
Although most of the time it just goes by feel, since with large input signal the behavior of many loudspeakers will drastically change anyway.
With certain T/S parameters you sometimes can't get anything that will fit well anyway.
For BP systems you can get ballpark figures out of a closed and/or BR design, as mentioned before.
These days most things will have some active EQ anyway. So optimizing for best acoustic fit isn't very useful.
I'd rather work with target curves.
Although most of the time it just goes by feel, since with large input signal the behavior of many loudspeakers will drastically change anyway.
With certain T/S parameters you sometimes can't get anything that will fit well anyway.
For BP systems you can get ballpark figures out of a closed and/or BR design, as mentioned before.
These days most things will have some active EQ anyway. So optimizing for best acoustic fit isn't very useful.
Hi @David McBean . I had some facebook discussion with Brian Steele and he mentioned asking you if there was a way to model Augmented Passive Radiator designs in HornResp? He did mention this was discussed and dismissed in the past as being very difficult. I'm researching the design for the InDIYana 2024 competition (so just for fun!) and I'm trying to learn how to model these enclosures. There are AES papers by Thomas L. Clarke showing the acoustic circuit for these designs (see screenshot), so I'm attempting to teach myself how to translate that into a circuit that can be modeled in LT Spice or something similar. I'm completely new to this kind of analysis, so I thought I'd reach out to see if you'd reconsider looking into this? Regardless of your answer, thanks for HornResp, and all your contributions to our hobby / profession!
Attachments
...and I just now actually searched for APRs in this thread. I hadn't realized the question was brought up only last month! Apologies for bringing that up again so soon, though if having the acoustic circuits helps I'd still like to know.
David,
Thank you so much for your time. Thanks a lot!
This is my formula:
Lv =((274,419*C)((D/2)2,54)^2/(Fb^2(Vb+Vp/5,6)))-(Ec((D/2)*2,54))
Try and you 'll see that it's very, very close to give me the Lv for real measured Fb for all Vb and Fb you use.
where:
Lv = Port lenght in cm
C = Sound Speed in m/s (in my case I used 30°C for temperature but the difference was not relevance - I used 346m/s in my test)
D = Diameter of the port in inches (I used 6 inches for all tests)
Fb = Port Freq. in Hz
Vb= Box Volume in liters
Vp = Port Volume in liters
Ec = End Correction (1,464 in this case)
So, what do you think about?
Last edited:
I tried your method, but I seem to get better results by dividing Vp by 3 in the equation to find the final value for Lp. I used the vent design equation from the LDC and kept all parameters metric for easier understanding. See example below.
| D | = | 10.16 | cm | |
| Ap | = | 81.1 | cm^2 | |
| Vb | = | 35.0 | litres | |
| Fb | = | 30.0 | Hz | |
| Lp1 | = | 69.1 | cm | Lp1=(9.425*10^4*(D/2)^2/(Fb^2*Vb))-1.595*(D/2) |
| Vp | = | 5.6 | litres | |
| cf | = | 0.33 | ||
| Lp | = | 65.2 | cm | Lp=(9.425*10^4*(D/2)^2/(Fb^2*(Vb+cf*Vp)))-1.595*(D/2) |
| Vt | = | 40.6 | litres |
Before making a decision either way I would need to see descriptions of all elements shown in the acoustic circuit diagram, and in particular those used to specify the augmented passive radiator. A copy of the complete AES paper would be even more helpful.
I tried to send you the papers in a direct message. Is there an email address that works?
Just to confirm, I assume that the formulas to actually use are as shown below, and that the original 5.5 constant has been changed to 5.6?
(The operators missing from your equation have been added in red).
For Step 1:
Lv1 = (274.419*C)x((D/2)x2.54)^2/((Fb^2)xVb)-Ecx((D/2)*2.54)
For Step 2:
Lv2 = (274.419*C)x((D/2)x2.54)^2/((Fb^2)x(Vb+Vp/5.6))-Ecx((D/2)*2.54)
If so, then for the small amount of testing I have done the method appears to be surprisingly accurate when Fb, Vb and D have realistic values.
Maybe the method should be added to Hornresp as a bass reflex loudspeaker design tool…🙂
Well done!
I dunno, I can't get "Vp/5.6" as a correction factor for Vp to work. "0.333*Vp", or "Vp/3" seems to work well however.
Note: the value of "1.464" for vent end-correction is 0.732+0.732, which assumes that both ends of the vent are "open", i.e. not attached to anything. The LDC assumes that one end of the vent is flanged (e.g. attached to the box), so instead it uses 0.863+0.732=1.595 for the vent end-correction. As the Hornresp model schematic shows one end of the vent connected to the chamber, I think 1.595 would be a more correct value to use for the vent end-correction.
One "gotcha" to look out for when testing this new equation is to ensure that Vp is fairly large compared to Vt, the total box size (Vb+Vp), otherwise the impact of Vp on the calculation for the new value of Lpt will be very small, and the choice of what value is used for the vent end-correction will have a larger impact on the calculated results. In the example below, I assumed a Vp of 25 liters and I used a large value for Ap, so Vp was basically 1/3rd of Vt.
See worked example below:
| c | = | 344.0 | m/s | |
| k | = | 274.419 | ||
| ec | = | 1.595 | Vent end correction, one end open, one flanged | |
| cf | = | 0.333 | ||
| Vb | = | 25.0 | litres | Net box volume |
| Ap | = | 81.0 | cm^2 | Vent cross-sectional area |
| Fb | = | 30.0 | Hz | Target resonance frequency |
| D | = | 10.2 | cm | D=2*(Ap/PI())^0.5 |
| R | = | 5.1 | cm | R=D/2 |
| Lpt' | = | 100.1 | cm | Lpt'=(k*c*R^2/(Fb^2*Vb))-ec*R |
| Vp | = | 8.1 | litres | Vp=Ap*Lpt'/1000 |
| Vb' | = | 27.7 | litres | Vb'=Vb+cf*Vp |
| Lpt | = | 89.5 | cm | Lpt=(k*c*R^2/(Fb^2*Vb'))-ec*R |
| Vt | = | 33.1 | litres | Vt=Vb+Vp |
| Vp/Vt | = | 0.32 |
... and, after adjusting Lpt in the Hornresp sim accordingly to match the calculated value for Lpt,...
Last edited:
"Note: the value of "1.464" for vent end-correction is 0.732+0.732, which assumes that both ends of the vent are "open", i.e. not attached to anything. The LDC assumes that one end of the vent is flanged (e.g. attached to the box), so instead it uses 0.863+0.732=1.595 for the vent end-correction. As the Hornresp model schematic shows one end of the vent connected to the chamber, I think 1.595 would be a more correct value to use for the vent end-correction."
Sigh. Turns out that might be wrong and the LDC itself might be wrong, at least where it quoted that particular equation (in the section concerning 4th order BP systems). I did some Googling on the subject, only to be reminded by the Internet of some information I'd provided on the issue years ago, LOL. The "correct" value should be 1.463. Fortunately that didn't change the results I posted in my previous message in any significant way. New table below. In hindsight it's fairly obvious that the end-correction factor should not be dependent on what standard is used for the dimensions (imperial or metric).
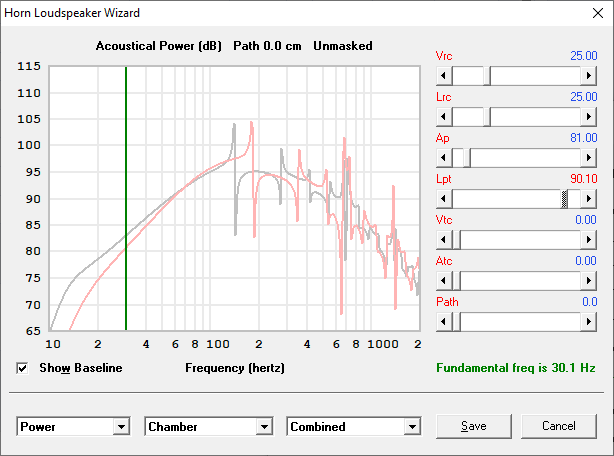
Of course, both the "new" equation AND Hornresp could be wrong about the predicted Fb for a volume Vb tuned by a tube of area Ap and length Lpt. But I'll leave that for another post 🙂
Sigh. Turns out that might be wrong and the LDC itself might be wrong, at least where it quoted that particular equation (in the section concerning 4th order BP systems). I did some Googling on the subject, only to be reminded by the Internet of some information I'd provided on the issue years ago, LOL. The "correct" value should be 1.463. Fortunately that didn't change the results I posted in my previous message in any significant way. New table below. In hindsight it's fairly obvious that the end-correction factor should not be dependent on what standard is used for the dimensions (imperial or metric).
| Metric | Imperial | Conv. | Check | |||||||
| c | = | 344.0 | m/s | 1128.6 | ft/s | = | 344.0 | m/s | 0.0 | |
| k | = | 274.419 | 12962.886 | |||||||
| ec1 | = | 0.425 | vent end correction (flanged) | 0.425 | ||||||
| ec2 | = | 0.307 | vent end correction (free) | 0.307 | ||||||
| ec | = | 0.732 | total vent end correction (flanged + free) | 0.732 | ||||||
| cf | = | 0.333 | vent length correction | 0.333 | ||||||
| Vb | = | 25.0 | litres | Box Volume | 1525.0 | cu.in. | = | 25 | litres | 0.0 |
| Ap | = | 81.0 | cm^2 | Vent Area | 12.6 | in.^2 | = | 81.0 | cm^2 | 0.0 |
| Fb | = | 30.0 | Hz | Target Resonance Frequency | 30 | Hz | ||||
| D | = | 10.2 | cm | D=2*(Ap/PI())^0.5 | 4.0 | in. | = | 10.2 | cm | 0.0 |
| R | = | 5.1 | cm | R=D/2 | 2.0 | in. | = | 5.1 | cm | 0.0 |
| Lpt' | = | 100.7 | cm | Lpt'=(k*c*R^2/(Fb^2*Vb))-ec*2*R | 39.7 | in. | = | 100.8 | cm | 0.0 |
| Vp | = | 8.2 | litres | Vp=Ap*Lpt'/1000 | 498.1 | cu.in. | = | 8.2 | litres | 0.0 |
| Vb' | = | 27.7 | litres | Vb'=Vb+cf*Vp | 1690.8 | cu.in. | = | 27.7 | litres | 0.0 |
| Lpt | = | 90.1 | cm | Lpt=(k*c*R^2/(Fb^2*Vb'))-ec*2*R | 35.5 | in. | = | 90.2 | cm | 0.0 |
Of course, both the "new" equation AND Hornresp could be wrong about the predicted Fb for a volume Vb tuned by a tube of area Ap and length Lpt. But I'll leave that for another post 🙂