There used to be a freeware called digitiz if I remember correctly that will grab plot lines off as numbers for Excell.
Thanks, I'll check it out.
Audition 3.0 (with a lot of bloating example projects) was distributed for free by Adobe quite some years ago, as part of the free CS2 bundle. One should be able to find it somewhere out there... the serial to be used is 1137-1004-8571-6848-7845-8029.
EDIt: Working versions of Audition 1.5 should be around also... I actually prefer its display style to 3.0 but it lacks ASIO support..,
Last edited:
Exactly my point.
The unexpected part was that the output from the filter is no longer the input frequency of 20Khz, but 17.5 Khz.
I am quite surprised you did not notice that.
jn
ps..mark, it is a consequence of filtering out one sideband, not nonlinearity of the sampling process. If the sideband is within the passband of the filter but the filter slope attenuates the upper sideband, the output will also not be the same as the input.
Last edited:
some Gibbs details for all...
Informally, the Gibbs phenomenon reflects the difficulty inherent in approximating a discontinuous function by a finite series of continuous sine and cosine waves. It is important to put emphasis on the word finite because even though every partial sum of the Fourier series overshoots the function it is approximating, the limit of the partial sums does not. The value of x where the maximum overshoot is achieved moves closer and closer to the discontinuity as the number of terms summed increases so, again informally, once the overshoot has passed by a particular x, convergence at that value of x is possible.
There is no contradiction in the overshoot converging to a non-zero amount, but the limit of the partial sums having no overshoot, because the location of that overshoot moves. We have pointwise convergence, but not uniform convergence. For a piecewise C1 function the Fourier series converges to the function at every point except at the jump discontinuities. At the jump discontinuities themselves the limit will converge to the average of the values of the function on either side of the jump. This is a consequence of the Dirichlet theorem.[11]
The Gibbs phenomenon is also closely related to the principle that the decay of the Fourier coefficients of a function at infinity is controlled by the smoothness of that function; very smooth functions will have very rapidly decaying Fourier coefficients (resulting in the rapid convergence of the Fourier series), whereas discontinuous functions will have very slowly decaying Fourier coefficients (causing the Fourier series to converge very slowly). Note for instance that the Fourier coefficients 1, −1/3, 1/5, ... of the discontinuous square wave described above decay only as fast as the harmonic series, which is not absolutely convergent; indeed, the above Fourier series turns out to be only conditionally convergent for almost every value of x. This provides a partial explanation of the Gibbs phenomenon, since Fourier series with absolutely convergent Fourier coefficients would be uniformly convergent by the Weierstrass M-test and would thus be unable to exhibit the above oscillatory behavior. By the same token, it is impossible for a discontinuous function to have absolutely convergent Fourier coefficients, since the function would thus be the uniform limit of continuous functions and therefore be continuous, a contradiction. See more about absolute convergence of Fourier series.
[]Bad title - Wikipedia
THx-RNMarsh
Informally, the Gibbs phenomenon reflects the difficulty inherent in approximating a discontinuous function by a finite series of continuous sine and cosine waves. It is important to put emphasis on the word finite because even though every partial sum of the Fourier series overshoots the function it is approximating, the limit of the partial sums does not. The value of x where the maximum overshoot is achieved moves closer and closer to the discontinuity as the number of terms summed increases so, again informally, once the overshoot has passed by a particular x, convergence at that value of x is possible.
There is no contradiction in the overshoot converging to a non-zero amount, but the limit of the partial sums having no overshoot, because the location of that overshoot moves. We have pointwise convergence, but not uniform convergence. For a piecewise C1 function the Fourier series converges to the function at every point except at the jump discontinuities. At the jump discontinuities themselves the limit will converge to the average of the values of the function on either side of the jump. This is a consequence of the Dirichlet theorem.[11]
The Gibbs phenomenon is also closely related to the principle that the decay of the Fourier coefficients of a function at infinity is controlled by the smoothness of that function; very smooth functions will have very rapidly decaying Fourier coefficients (resulting in the rapid convergence of the Fourier series), whereas discontinuous functions will have very slowly decaying Fourier coefficients (causing the Fourier series to converge very slowly). Note for instance that the Fourier coefficients 1, −1/3, 1/5, ... of the discontinuous square wave described above decay only as fast as the harmonic series, which is not absolutely convergent; indeed, the above Fourier series turns out to be only conditionally convergent for almost every value of x. This provides a partial explanation of the Gibbs phenomenon, since Fourier series with absolutely convergent Fourier coefficients would be uniformly convergent by the Weierstrass M-test and would thus be unable to exhibit the above oscillatory behavior. By the same token, it is impossible for a discontinuous function to have absolutely convergent Fourier coefficients, since the function would thus be the uniform limit of continuous functions and therefore be continuous, a contradiction. See more about absolute convergence of Fourier series.
[]Bad title - Wikipedia
THx-RNMarsh
Since it appears I'm in a good mood today, instead of replying to T-E with another "Sit, T-E, sit", here are some clues:
True, maybe news to you, otherwise known for about 100 years. There is nothing special in this example of violating Nyquist.
That's something that should be decided based on audibility. Examples shown herein are illustrating that the amount of energy carried by a recorded cymbal sound (at high sample rate) over the 22.05KHz CD Nyquist limit is very small. This, combined with the lack of proof and an accepted mechanism on how ultrasonic components are affecting the listener experience (ignore the Oohashi crap please) are leading to the logical conclusion that it does not. As logical as shifting the burden of proof on those claiming it does, as an extraordinary claim.
No, not necessary, unless somebody can prove that it matters for the listener experience, see the previous point.
You seem to miss the essential detail that adding two sine signals IS NOT modulation. The spectrum of two sines added is exactly two delta impulses at f1 and f2. Modulation essentially requires a non linear process, either in the analog domain (a "modulator", like the exponential characteristic of a transistor BE junction) or in the digital domain (like in the sampling process itself). Only a modulated signal spectrum will show the carrier and the two side bands at f1-f2 and f1+f2.
There is absolutely nothing special in an AM signal violating Nyquist, so the upper side band may be removed by the brickwall filter. It is unclear why you need Hans or anybody else to try anything in particular about such signals, if the outcome is predictible, to the point of being obvious. That is, removing the upper side band of an AM signal is known as a SSB signal (or with the carrier also supressed, SSB-SC), and is for example widely used in Software Defined Radios as an AM signal demodulation method. If you believe that such an AM modulated signal is usually encountered in audio recordings, and removing its upper side band is affecting the listener experience, then you better come up with some proof before making any further claims.
True, maybe news to you, otherwise known for about 100 years. There is nothing special in this example of violating Nyquist.
That's something that should be decided based on audibility. Examples shown herein are illustrating that the amount of energy carried by a recorded cymbal sound (at high sample rate) over the 22.05KHz CD Nyquist limit is very small. This, combined with the lack of proof and an accepted mechanism on how ultrasonic components are affecting the listener experience (ignore the Oohashi crap please) are leading to the logical conclusion that it does not. As logical as shifting the burden of proof on those claiming it does, as an extraordinary claim.
No, not necessary, unless somebody can prove that it matters for the listener experience, see the previous point.
You seem to miss the essential detail that adding two sine signals IS NOT modulation. The spectrum of two sines added is exactly two delta impulses at f1 and f2. Modulation essentially requires a non linear process, either in the analog domain (a "modulator", like the exponential characteristic of a transistor BE junction) or in the digital domain (like in the sampling process itself). Only a modulated signal spectrum will show the carrier and the two side bands at f1-f2 and f1+f2.
There is absolutely nothing special in an AM signal violating Nyquist, so the upper side band may be removed by the brickwall filter. It is unclear why you need Hans or anybody else to try anything in particular about such signals, if the outcome is predictible, to the point of being obvious. That is, removing the upper side band of an AM signal is known as a SSB signal (or with the carrier also supressed, SSB-SC), and is for example widely used in Software Defined Radios as an AM signal demodulation method. If you believe that such an AM modulated signal is usually encountered in audio recordings, and removing its upper side band is affecting the listener experience, then you better come up with some proof before making any further claims.
Last edited:
sigh...just look at the plot.. 20Khz in, 17.5 Khz out.
And now, your trying to reduce a technical discussion into "is it audible"?
LOL.
jn
And now, your trying to reduce a technical discussion into "is it audible"?
LOL.
jn
Last edited:
1.5 worked under XP as did Cooledit. Then one day, I don't quite remember when the Win Audio No Fun started.
Which is fine..
I have already stated that I have never noticed any difference in CD format. so for me, inaudible..But that's just me.
I never ever considered this envelope based concept before, and apparently nobody else has (that I'm aware of) in the last 40 years w/r to CD sampling rate and consequent filtering needs. So, if it is happening with some music content, nobody has been looking for it.
Now that we know this problem can arise for purposely oddball audio signals, the knowledge is there to examine actual musical content.
I suspect the focus on cymbals as in the other thread is no coincidence.
jn
This is confusing. You talk about AM and addition as if the same thing. Adding 2sines does not create another freq. I can see your point and agree that the envelope may be altered but the above does not clear things up. The question becomes: how fast ( and probably what shape) does the envelope have to be to violate nyquist.
Last edited:
This is all you have to say? You just killed my mood. At this point, I have to re-state what Hans and others already mentioned. I do not understand the point(s) you are trying to make (and apparently nobody else does), and, watching your tactics over the last 10 days (of shifting the focus all along, obfuscating, "that's not what I said", quoting irrelevant data, etc...), I believe you are only attempting to stir the pot, since I refuse to accept you are that obtuse to any arguments.
And yes, as I already mentioned, ultimately it is about audibility, since nothing you are trying to convey, in an obfuscated way, is new, unknown, or anywhere more relevant to digital audio then it is for any other DSP application.
And that's because it is a totally useless concept, for audio and any other DSP application. If you would care to follow what was told to you by multiple contributors here you would quickly realize this fact. Sorry to mention, you "discovered" absolutely nothing that is worth discussing with anybody aware of DSP, you may find an auditory with the T-E's and Richard's of the world (which you already did, BTW).
LOL.
Last edited:
Actually it is a progress; last time it was even "facts are evaluated by how a group of believers receives them" (words to that effect) (SCR)
Ignoring the Oohashi crap means (as today) to ignore a whole bunch of experiment done in each year (since the original publication) and in various fields (Lehnhardt comes to mind for example), but if one isn't following the literature it gets difficult too.
"Extraordinary claim" seems to be another differently seen topic. What makes a claim "extraordinary" ? A reasonable approach would be that overwhelming factual experimental evidence contradicting the claim is existent; a "don't want that it is" is surely not sufficient.
But of course, at the end, the audibility is important, and it was the start of this discussion IIRC.... 🙂
@RNMarsh,
Wrt Gibbs, another one to read;my understanding so far of the Gibbs Phenomenon was indeed that the magnitude of the overshoot (~ 9%) remains constant even when approachen infinity (means sum of terms).
The wavelength of the ringing gets shorter and shorter with an increasing number of terms but not the magnitude.
Of course the energy wise it is a reduction...
Last edited:
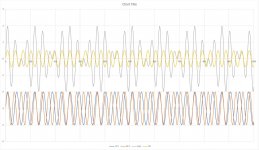
A clarification on the bolded part..I put a sheet together to add two frequencies.
Blue is 17.5 Khz
Orange is 22.5 Khz
Grey is the addition of the two
yellow is 20 Khz.
Note that the sum of 17.5 and 22.5 undergoes a 180 degree flip every time red and blue sum to zero.
That is absolutely the correct question.
jn
Attachments
Last edited:
The usual question is about preferring smart but rather undisciplined over mediocre but disciplined. I normally prefer the former, but now I realize that by replacing "indisciplined" with "stubborn", I may give it a second thought.
Last edited:
You may be surprised I made it through a very successful 40 years career, being now too close to retirement than I would like.
Sit, T-E.
I've read him. His ""eyes-as-fenestrations-to-the-ears-a-novel-mechanism-for-highfrequency-and-ultrasonic-hearing. "" was rather startling. If I go 90 miles south of key west, I'm taking acrylic goggles with me..
jn
ps..scottjoplin, that animation is just so cool, thanks.
Last edited:
- Status
- Not open for further replies.