I don't want to be unkind with you, but this way is extremely difficult to have a technical discussion.
I need to teach you Classical Electrodynamics on over a few post on an audio forum, something impossible, but in order to give correct information, and for the good of this community, I will give you a proper answer with the hope that you stop to write nonsense.
No, this is nonsense, let me explain
By definition in Topology
A loop it is a path whose initial point is equal to the terminal point.
So we can say that a loop is a closed curve.
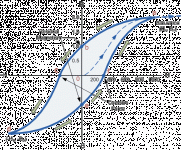
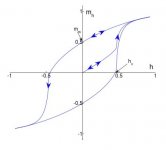
As we seen before, a DC magnetic field has an open magnetic hysteresis curve B=f(H) (#)
As we seen before, an AC magnetic field has a closed magnetic hysteresis curve B=f(H), AKA hysteresis loop.
(#) Supposing that DC current increases from zero to certain positive value and after this value is reached it is maintained constant.
No, this is also nonsense, let me explain
As we seen before
Then the slope of a line tangent to a point on a magnetic hysteresis curve B=f(H) represents the magnetic permeability.
Magnetization, M, is defined as
Combining (*) and (**) we can write
Or
χ is called magnetic susceptibility
Then the slope of a line tangent to a point on a magnetization curve M=f(H) represents the magnetic susceptibility.
Note that when μ is a tensor, we can't make malabars and the intermediate pass is no longer possible on that form, however the last relation is still valid and χ is also a tensor.
Maxwell's Equations
Are LINEAR, then we can apply linear superposition principle.
The linear superposition principle applies to any linear system, including algebraic equations, linear differential equations, and systems of equations of those forms.
The stimuli and responses could be numbers, functions, vectors, vector fields, time-varying signals, or any other object.
Note that when vectors or vector fields are involved, a superposition is interpreted as a vector sum.
Even in the case that μ is a tensor, it can be represented by a matrix, the product of a matrix for a vector is another vector,...Linear Algebra...
As an example where seems impossible to apply linear superposition, let's consider highly nonlinear Coulomb's law
Then the electric field at point x due to a charge at point x1
By linear superposition, suppose n charges qi at points xi, i=1,...n, the electric field
But don't worry, even in the case when μ is a tensor, we can use a dirty trick.
The problem here, as I said before, is that the constitutive relation (*) is not a single valued function, so we can take both path of the loop separately, one ascendant and the other descendant, so no problem at all.
I need to teach you Classical Electrodynamics on over a few post on an audio forum, something impossible, but in order to give correct information, and for the good of this community, I will give you a proper answer with the hope that you stop to write nonsense.
No, this is nonsense, let me explain
By definition in Topology
A loop it is a path whose initial point is equal to the terminal point.
So we can say that a loop is a closed curve.
As we seen before, a DC magnetic field has an open magnetic hysteresis curve B=f(H) (#)
As we seen before, an AC magnetic field has a closed magnetic hysteresis curve B=f(H), AKA hysteresis loop.
(#) Supposing that DC current increases from zero to certain positive value and after this value is reached it is maintained constant.
No, this is also nonsense, let me explain
As we seen before
B = μ H (*)
Then the slope of a line tangent to a point on a magnetic hysteresis curve B=f(H) represents the magnetic permeability.
Magnetization, M, is defined as
B = H + 4π M (**)
Combining (*) and (**) we can write
M = [(μ - 1) / 4π] H
Or
M = χ H
χ is called magnetic susceptibility
Then the slope of a line tangent to a point on a magnetization curve M=f(H) represents the magnetic susceptibility.
Note that when μ is a tensor, we can't make malabars and the intermediate pass is no longer possible on that form, however the last relation is still valid and χ is also a tensor.
Maxwell's Equations
∇.D = 4π ρ
∇.B = 0
∇xE + (1/c) ∂B/∂t = 0
∇xH - (1/c) ∂D/∂t = (4π/c) J
∇.B = 0
∇xE + (1/c) ∂B/∂t = 0
∇xH - (1/c) ∂D/∂t = (4π/c) J
Are LINEAR, then we can apply linear superposition principle.
The linear superposition principle applies to any linear system, including algebraic equations, linear differential equations, and systems of equations of those forms.
The stimuli and responses could be numbers, functions, vectors, vector fields, time-varying signals, or any other object.
Note that when vectors or vector fields are involved, a superposition is interpreted as a vector sum.
Even in the case that μ is a tensor, it can be represented by a matrix, the product of a matrix for a vector is another vector,...Linear Algebra...
As an example where seems impossible to apply linear superposition, let's consider highly nonlinear Coulomb's law
F = k q1 q2 (x1 - x2) / ∣x1 - x2∣³
Then the electric field at point x due to a charge at point x1
E(x) = k q1 (x - x1) / ∣x - x1∣³
By linear superposition, suppose n charges qi at points xi, i=1,...n, the electric field
E(x) = ∑ qi (x - xi) / ∣x - xi∣³ (k=1, cgs units)
But don't worry, even in the case when μ is a tensor, we can use a dirty trick.
The problem here, as I said before, is that the constitutive relation (*) is not a single valued function, so we can take both path of the loop separately, one ascendant and the other descendant, so no problem at all.
Attachments
Last edited:
I agree that an AC stimulus is required to create a loop but it is important to understand that the graphical representation of a DC curve is derived from a series of AC loops with increasing value.
OMG, what have I done to deserve this punishment? 
So far, Classical Electrodynamics, now Nuclear Magnetic Resonance!!!
Forum people will want to kill me, and I don't know much about NMR, but here we go...😀
Let's suppose now that behavior of our transformer core is like water.
Let's consider a system of nuclear spins immersed in an external magnetic field Hdc in thermodynamic equilibrium with the network.
If we denote by p the nuclear spin angular momentum, the equation of motion of the magnetic moment l in a magnetic field H will be as follows
Multiplying both sides by c, and considering that
We obtain
If you put an external field Hdc, at molecular level, the magnetic moment l, precesses around the external field Hdc at the Larmor frequency, and this is called Larmor precession.
We can not consider isolated nuclear momentum, but at most in nuclear arrangements containing a large number of identical nuclei and also, in the equilibrium, these nuclei are distributed among energy levels according to the Boltzmann distribution, that distribution favors the lowest energy states with which, at equilibrium more nuclei will be aligned in the direction of Hdc, than the opposite; consequently there will be a net macroscopic magnetization Mdc, oriented in the direction of the field Hdc.
If now M is the vector sum of all l, then adding vectorially on both sides of equation (*) over all l we obtain
Clearly we see that if M=Mdc and H=Hdc, because Mdc // Hdc, then MdcxHdc=0, then
The macroscopic magnetization remains static, as the magnetization curve is a succession of equilibrium states, magnetization curve will be a succession of static macroscopic magnetization, so DC magnetic hysteresis curve will be a succession of static states.
Sorry, so far the answer is no, at least macroscopically.
What happens if now our core is ferromagnetic again?
In a ferromagnetic material the degree of alignment of the electron spins between neighboring atoms is high as a result of a force that tends to lock the spins of these electrons in a parallel direction, this force is so strong that the spins remain aligned even when the external magnetic field is removed.
Every single magnetic moment l, will remain fix "as curls of statue" in the direction of Hdc, forget precession.
Then, the answer is NO, even at molecular level.
Your affirmation requires that is applied another magnetic field Hac, simultaneously with Hdc.
And please, stop to write nonsense!
So far, Classical Electrodynamics, now Nuclear Magnetic Resonance!!!
Forum people will want to kill me, and I don't know much about NMR, but here we go...😀
Let's suppose now that behavior of our transformer core is like water.
Let's consider a system of nuclear spins immersed in an external magnetic field Hdc in thermodynamic equilibrium with the network.
If we denote by p the nuclear spin angular momentum, the equation of motion of the magnetic moment l in a magnetic field H will be as follows
dp/dt = l x H
Multiplying both sides by c, and considering that
l = c p
We obtain
dl/dt = c l x H (*)
If you put an external field Hdc, at molecular level, the magnetic moment l, precesses around the external field Hdc at the Larmor frequency, and this is called Larmor precession.
We can not consider isolated nuclear momentum, but at most in nuclear arrangements containing a large number of identical nuclei and also, in the equilibrium, these nuclei are distributed among energy levels according to the Boltzmann distribution, that distribution favors the lowest energy states with which, at equilibrium more nuclei will be aligned in the direction of Hdc, than the opposite; consequently there will be a net macroscopic magnetization Mdc, oriented in the direction of the field Hdc.
If now M is the vector sum of all l, then adding vectorially on both sides of equation (*) over all l we obtain
dM/dt = c M x H
Clearly we see that if M=Mdc and H=Hdc, because Mdc // Hdc, then MdcxHdc=0, then
dM/dt = 0
The macroscopic magnetization remains static, as the magnetization curve is a succession of equilibrium states, magnetization curve will be a succession of static macroscopic magnetization, so DC magnetic hysteresis curve will be a succession of static states.
Sorry, so far the answer is no, at least macroscopically.
What happens if now our core is ferromagnetic again?
In a ferromagnetic material the degree of alignment of the electron spins between neighboring atoms is high as a result of a force that tends to lock the spins of these electrons in a parallel direction, this force is so strong that the spins remain aligned even when the external magnetic field is removed.
Every single magnetic moment l, will remain fix "as curls of statue" in the direction of Hdc, forget precession.
Then, the answer is NO, even at molecular level.
Your affirmation requires that is applied another magnetic field Hac, simultaneously with Hdc.
And please, stop to write nonsense!
Last edited:
"Let's suppose now that behavior of our transformer core is like water"
Amorphous cores ? 😀
Amorphous cores ? 😀
Last edited:
no amount of math will change the fundamentals.
Permeability can be graphically represented in two different ways.
Taking the dB/dH of a minor loop
Taking the dB/dH of a line tangent to a point on the magnetizing curve.
Taking the slope of a line tangent to a point on a hysteresis loop does not represent permeability, it is the deltaB/deltaH of the entire loop that does.
dave
Permeability can be graphically represented in two different ways.
Taking the dB/dH of a minor loop
Taking the dB/dH of a line tangent to a point on the magnetizing curve.
Taking the slope of a line tangent to a point on a hysteresis loop does not represent permeability, it is the deltaB/deltaH of the entire loop that does.
dave
I don't believe that those authors are so confused as you are, so please read them again.
Because of your poor understanding about physics, you are confused again, let me explain
Mathematics is THE language of Physics, so that "math" don't change the fundamentals because they ARE the fundamentals.
No, this is poorly expressed, let me explain
The derivative, is a local property of the curve, then you must say
Taking dB/dH at a point of the magnetic hysteresis curve B=f(H)
This is similar to your last sentence, but even more poorly expressed, let me explain
The derivative of a curve at a given point coincides with the slope of the straight line tangent to the curve at this point.
An amazingly good book you also can read is
Calculus, 4th edition: Michael Spivak: 9780914098911: Amazon.com: Books
Michael Spivak - Wikipedia, the free encyclopedia
Also you screwed up with the loop, here, as I said before, magnetization curve M=f(H) has nothing to do with magnetic permeability, but with magnetic susceptibility.
Magnetic susceptibility - Wikipedia, the free encyclopedia
No, this is also nonsense
Δμ = ΔB/ΔH
Is defined as "incremental permeability"
Permeability (electromagnetism) - Wikipedia, the free encyclopedia
Last edited:
yeah, concentrate on a better transformer design.
Juan, till so far you gave very good inside information on how a transformer works.
Why a low Bdc-Bac transformer is not always a good choice, bigger core is not always better, top!
As a designer you have to make a choice what you want in a design. Normally my choice is a Bdc is in the range 0.7T-0.9T . I like to have a flat response till 20Hz and my Bac would be not more as 0.7T - 0.9T.
What core losses are acceptable? What copper loss is good enough? Core loss depends on the core material and the frequency, copper losses not.
Is there a benefit for exotic core material as amorphous or nanocrystalline?
Juan, till so far you gave very good inside information on how a transformer works.
Why a low Bdc-Bac transformer is not always a good choice, bigger core is not always better, top!
As a designer you have to make a choice what you want in a design. Normally my choice is a Bdc is in the range 0.7T-0.9T . I like to have a flat response till 20Hz and my Bac would be not more as 0.7T - 0.9T.
What core losses are acceptable? What copper loss is good enough? Core loss depends on the core material and the frequency, copper losses not.
Is there a benefit for exotic core material as amorphous or nanocrystalline?
Last edited:
Yes, was a long night and a bad day, calculations take time, but because my Tarzan-English to write each post take me ages... 😱
Thanks for your encouragement. 🙂
As for transformers, working at small magnetic fields is not a bad idea, the problem is that requires enormous cores, unless you decide increase the number of turns; with a few examples I intended to show that biggest cores are not always the best option.
Your particular choice seems very good to me, as you can obtain good quality C cores, this is a great advantage, provided that Bmax=Bdc+Bac is below saturation region.
As for my own rule of dumb, I try to maintain total losses < 10%, copper losses about 6% in about equal parts for primary and secondary, it left for core losses < 4%. Of course, if you can reduce losses, much better, but with lamination I can obtain on this side of the world is very difficult.
As modern materials are so good and you can obtain ridiculously thin lamination, I don't care eddy current losses, but hysteresis losses are horrible, because they are so nonlinear.
Be concerned by hysteresis losses at lowest frequency, as you increase frequency, above certain value, it is as if you have not a core anymore.
Be concerned by copper losses at highest frequency, as you increase frequency, due to Skin effect, also does copper losses.
Finally, always do all the math, regardless how difficult can be, to evaluate the result, you can take a look to Partridge formula on post#2, even when distortion coefficient of the magnetic material were not available, you can make comparisons and usefull guesses.
Maybe in the future, when its properties will be improved, so far its major advantage is lower losses, however its prices make me look to other side.
Be in mind that our venerable Kondo-san was an expert metallurgist, and his election was exquisite Japanese C cores. AFAIK
Maybe it's just me, but the most annoying part of this otherwise interesting thread is the unending accusations that people are "confused".
I don't buy into the excuse you have "Tarzan English". You have a choice, you can either disagree with someone, or you can get personal and call them a derogatory name/adjective. Dave and 45 are certainly not "confused", nor do they have a "poor understanding" in fact, they are not anything that someone with Tarzan English should attempt to describe.
Please state your argument without calling them anything. Do not assign a name to them, nor state how pathetic their knowledge is. If you must insist, respectfully say "I disagree" and leave it at that.
This should not be difficult for a non-native English speaker to comprehend.
I don't buy into the excuse you have "Tarzan English". You have a choice, you can either disagree with someone, or you can get personal and call them a derogatory name/adjective. Dave and 45 are certainly not "confused", nor do they have a "poor understanding" in fact, they are not anything that someone with Tarzan English should attempt to describe.
Please state your argument without calling them anything. Do not assign a name to them, nor state how pathetic their knowledge is. If you must insist, respectfully say "I disagree" and leave it at that.
This should not be difficult for a non-native English speaker to comprehend.
On post#277 offensive word was "displeasure"
Now "confused" and "poor understanding" seems to be the major offenders.
Synonyms taken from Oxford Dictionaries
displeasure: annoyance, irritation, crossness, infuriation, anger, vexation, wrath, pique, chagrin, rancour, resentment, indignation, exasperation; dissatisfaction, discontent, discontentment, discontentedness, disgruntlement, disfavour, disapproval, disapprobation, disgust, distaste, offence, perturbation, disturbance, discomposure, upset, dismay
confused: bewildered, bemused, puzzled, perplexed, baffled, stumped, mystified, stupefied, nonplussed, muddled, befuddled, fuddled, dumbfounded, at sea, at a loss, at sixes and sevens, thrown (off balance), taken aback, disoriented, disconcerted, discomposed, troubled, discomfited, unnerved, shaken, shaken up, dazed, stunned, astonished, astounded
poor understanding: No results
But maybe used this way should be better and kinder
http://www.diyaudio.com/forums/tubes-valves/250569-transformer-test-10.html#post3818127
Maybe moderators should delete this smiley 😕
Honestly I do not think them neither offensive nor pejorative.
However if you please suggest more appropriate words, I gladly will use them from now. 😉
As for my Tarzan-English, it's a classic here, I "learned" English and French at high school, but without Google Translator I am really lost, and everybody who has used Google Translator knows that is easier to obtain a PhD than to make correct phrases with it, to illustrate the point, right now I am correcting my post, so far I used about one hour !
Without giving names, on this thread I suffered:
Bullying, Harassing, Trolling, Intentionally posting incorrect information, all of them against forum rules.
And now this underhand attack from you, to my use of language, that is not my native language.
I am more interested on equations, and without any intention to offend you, seems to me this attack, in addition to attack to suggested bibliography, are the major nonsense since my early days in this forum.
The only reason that I don't ask to moderators to disable my account, is that there are also good and friendly people, whom my humble contribution could be useful, who knows.
The moderators will not vet technically, its a stated policy. Every side's argument based on some technical approach that is not wrapped in strong personal attack commentary is considered additional info for the reader to decide upon its usefulness.
Gentlemen, take each other in your stride please, this is a public forum, there will be different and argumentative narrations on the tech or practical aspects of theories and designs as always.
The team has watched all the reported items till now and did not find them rules breaking.
Gentlemen, take each other in your stride please, this is a public forum, there will be different and argumentative narrations on the tech or practical aspects of theories and designs as always.
The team has watched all the reported items till now and did not find them rules breaking.
It turns out Ruben Lee's book is out of copyright to the images and text are fair game. (thanks Westinghouse and Mr. Lee for the gift) The EE staff at MIT does a better treatment as does Bozorth but Lee did concentrate on audio transformers and that seems to the topic.
the book is at this link.https://archive.org/stream/ElectronicTransformersAndCircuits/Lee1955ElectronicTransformersAndCircuits#page/n37/mode/2up
OK... first the point I have been trying to get across in my words using Lee's illustrations:
Here we have a series of hysteresis loops with increasing amplitude. The normal magnetization curve traverses the tips (B'm B''m B'''m) of the minor loops. The slope of a line drawn on any point of this curve through the origin determines permeability.
Here are some normal permeability measurements showing core nonlinearity. Note that this is done on the magnetization curve and not the BH loop. Also note that the line to determine the permeability extends through the origin. If you consider how the magnetization curve was derived this makes perfect sense.
The permeabilites shown are the initial permeability and the maximum permeability.
Now lets consider adding DC into the mix and we get a displaced minor loop. Again the u is dB/dH of the entire loop and not determined by the slope of a line tangent to a point on the loop.
My initial objection was to this graphical treatment from post #182
this pretty clearly states that there is a magnetization curve and a minor hysteresis loop. They are not drawn correctly but the point is understood.
Then this is presented in post 235
note how the u(ac) is being determined by the slope of a BH loop which is at complete odds with the classic theory of graphically calculating u(ac)
below are the three pages from Lee.
the book is at this link.https://archive.org/stream/ElectronicTransformersAndCircuits/Lee1955ElectronicTransformersAndCircuits#page/n37/mode/2up
OK... first the point I have been trying to get across in my words using Lee's illustrations:
Here we have a series of hysteresis loops with increasing amplitude. The normal magnetization curve traverses the tips (B'm B''m B'''m) of the minor loops. The slope of a line drawn on any point of this curve through the origin determines permeability.
Here are some normal permeability measurements showing core nonlinearity. Note that this is done on the magnetization curve and not the BH loop. Also note that the line to determine the permeability extends through the origin. If you consider how the magnetization curve was derived this makes perfect sense.
The permeabilites shown are the initial permeability and the maximum permeability.
Now lets consider adding DC into the mix and we get a displaced minor loop. Again the u is dB/dH of the entire loop and not determined by the slope of a line tangent to a point on the loop.
My initial objection was to this graphical treatment from post #182
Bdc=f(Hdc) curve is from point O to A, Bac=f(Hac) curve is magnetic hysteresis loop, its path follows A-B-C-D-A points.
this pretty clearly states that there is a magnetization curve and a minor hysteresis loop. They are not drawn correctly but the point is understood.
Then this is presented in post 235
As now elementary math has abandoned us, due to magnetic anisotropy, we only can do a graphical description.
At each point on the B=f(H) curve, must be
B = μ H
Then μ(AC) is the "slope" of the curve at each point.
note how the u(ac) is being determined by the slope of a BH loop which is at complete odds with the classic theory of graphically calculating u(ac)
below are the three pages from Lee.
Please let me clarify that I have not any complaint against moderators at all.
Also I want clarify that between post#16 and post#213, has been deleted about ten posts.
Surely I have a distorted vision of forum rules, and maybe I am a bit over sensitive.
My sincere apologies to moderation team.
Magnetic permeability was defined by physicists, the term was coined in September, 1885 by Oliver Heaviside, and since then this is its name "magnetic permeability"
Coincidentally, this same magnetic permeability, is that I have been using from post#1.
Such things as "normal permeability" or "incremental permeability" does not exist in real world.
Indeed core/lamination manufacturers simply use magnetic permeability, the true one.
Please, see for yourself
http://www.nssmc.com/product/catalog_download/pdf/D004je.pdf
Yes, the Japanese also confuse B with M, only that with its alphabet have a good alibi. 😀
BTW, manufacturers only can give DC magnetic permeability, because it is almost impossible give AC magnetic permeability, one loop for each frequency, an a lot of values for each loop on each point...would be insane!
Sorry, but I can't see magnetization M anywhere. 😕
Neither I can see magnetic permeability. 😕
Sorry, but I can't see magnetization M anywhere. 😕
Where is magnetic permeability? 😕
It says "Normal permeabilities" 🙄
Beautiful drawing, but I can't see magnetic permeability anywhere. 😕
It says "Incremental permeability" 🙄
BTW, my drawing looks like an UFO 😀
😕
Coincidentally, this same magnetic permeability, is that I have been using from post#1.
Such things as "normal permeability" or "incremental permeability" does not exist in real world.
Indeed core/lamination manufacturers simply use magnetic permeability, the true one.
Please, see for yourself
http://www.nssmc.com/product/catalog_download/pdf/D004je.pdf
Yes, the Japanese also confuse B with M, only that with its alphabet have a good alibi. 😀
BTW, manufacturers only can give DC magnetic permeability, because it is almost impossible give AC magnetic permeability, one loop for each frequency, an a lot of values for each loop on each point...would be insane!
Here we have a series of hysteresis loops with increasing amplitude. The normal magnetization curve traverses the tips (B'm B''m B'''m) of the minor loops. The slope of a line drawn on any point of this curve through the origin determines permeability.
Sorry, but I can't see magnetization M anywhere. 😕
Neither I can see magnetic permeability. 😕
Here are some normal permeability measurements showing core nonlinearity. Note that this is done on the magnetization curve and not the BH loop. Also note that the line to determine the permeability extends through the origin. If you consider how the magnetization curve was derived this makes perfect sense.
The permeabilites shown are the initial permeability and the maximum permeability.
Sorry, but I can't see magnetization M anywhere. 😕
Where is magnetic permeability? 😕
It says "Normal permeabilities" 🙄
Now lets consider adding DC into the mix and we get a displaced minor loop. Again the u is dB/dH of the entire loop and not determined by the slope of a line tangent to a point on the loop.
Beautiful drawing, but I can't see magnetic permeability anywhere. 😕
It says "Incremental permeability" 🙄
BTW, my drawing looks like an UFO 😀
It is said that a picture is worth a thousand words, mine are worth only a hundred! 😀
😕
Last edited:
No, you are confused...no just kidding. 😀
Let me explain, "I disagree" can be very academic, but...how to say...it sounds a bit sissy to my taste.
I prefer a more powerful like "I strongly disagree" if you will allow me.
Tip#10 Reducing copper loss at high frequency
For a given frequency, electrons has the bad habit to travel near of wire surface, this is known as Skin effect.
The skin depth δ, is thus defined as the depth below the surface of the conductor at which the current density has fallen to 1/e
Where
δ is the skin depth [δ]=mm
ρ = 0.017 (Ω mm2) / m , copper resistivity.
μ ≈ 1 is the magnetic permeability of copper [μ]=dimensionless
ω = 2 π f
At 100KHz, for copper, δ≈0.23mm
Then do not make sense to use too thick wires.
For a given frequency, electrons has the bad habit to travel near of wire surface, this is known as Skin effect.
The skin depth δ, is thus defined as the depth below the surface of the conductor at which the current density has fallen to 1/e
δ ≈ √(2 ρ / μ ω)
Where
δ is the skin depth [δ]=mm
ρ = 0.017 (Ω mm2) / m , copper resistivity.
μ ≈ 1 is the magnetic permeability of copper [μ]=dimensionless
ω = 2 π f
At 100KHz, for copper, δ≈0.23mm
Then do not make sense to use too thick wires.
- Status
- Not open for further replies.